Байесовские методы машинного обучения (Спецсеминар)
Материал из MachineLearning.
Основные направления работы семинара
Семинар (рук. доц. каф. ММП ф-та ВМК МГУ, к.ф.-м.н. Д.П. Ветров, н.с. каф. ММП ф-та ВМК МГУ Д.А. Кропотов, асп. ВМК МГУ М.В. Фигурнов) проводится для студентов каф. ММП, ф-та ВМК МГУ, но открыт для всех желающих. Основным направлением работы семинара является исследование и применение т.н. байесовского подхода к теории вероятностей в решении задач машинного обучения и компьютерного зрения. Байесовские методы получили большое распространение в мире в течение последних 15 лет. Их основными достоинствами являются
- возможность автоматической настройки структурных параметров алгоритмов машинного обучения (выбор количества кластеров, определение коэффициента регуляризации, отбор релевантных признаков и объектов, определение топологии нейросети и пр.);
- корректная работа с фактами, достоверность которых точно неизвестна, позволяющая обобщить методы классической булевой логики на ситуации, содержащие значительный элемент неопределенности, которая позволяет успешно применить байесовские методы в экспертных системах;
- возможность учета структурных и вероятностных взаимосвязей в массивах данных, опирающаяся на активно развиваемый в настоящее время аппарат графических моделей;
- представление данных и настраиваемых параметров, позволяющее объединять результаты наблюдений косвенных показателей неизвестной величины с априорными представлениями о ее характерных значениях.
Участники спецсеминара активно участвуют в теоретической работе по разработке новых методов настройки структурных параметров и алгоритмов машинного обучения для нестандартных задач, а также занимаются прикладными исследованиями в области когнитивных технологий.
Методическая поддержка спецсеминара осуществляется спецкурсом «Байесовские методы машинного обучения» и курсом «Графические модели», читаемых на факультете ВМК.
На сайте bayesgroup.ru располагается информация на английском языке об участниках спецсеминара и проводимых ими исследованиях.
Расписание спецсеминара
| | Рассылка сообщений о планируемых семинарах осуществляется в Гугл-группе «Bayesian methods research group seminar (vetrovsem)» |
Весенний семестр 2015 года
Осенний семестр 2014 года
Весенний семестр 2014 года
Осенний семестр 2013 года
Весенний семестр 2013 года
Осенний семестр 2012 года
Весенний семестр 2012 года
Осенний семестр 2011 года
Весенний семестр 2011 года
Осенний семестр 2010 года
Прикладные проекты
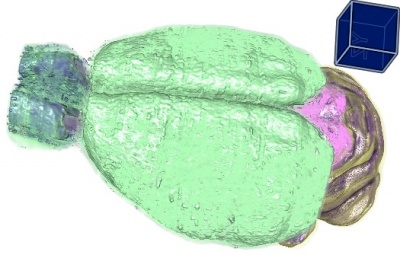
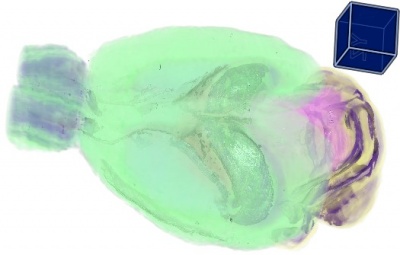
Построение трехмерной модели мозга мыши и статистический анализ экспрессии генов в мозге
Согласно современным представлениям когнитивные процессы определяются экспрессией генов в определенных областях головного мозга. В настоящее время биологи могут
- наблюдать в каких клетках происходит экспрессия того или иного гена
- определять за синтез какого белка отвечает тот или иной ген
- блокировать синтез соответствующего белка при помощи специальных препаратов
Уровень экспрессии генов можно определять только на препарированных срезах, поэтому эксперименты проводятся только на лабораторных животных, в частности на мышах.
Для получения биологических результатов требуется проводить статистический анализ экспрессии генов с учетом знаний о принадлежности клеток к различным анатомическим структурам головного мозга. Разработку соответсвующего метода мы разбили на несколько этапов:
- Построение трехмерной модель эталонного мозга. По результатам этого этапа были сделаны доклады на ММРО-14, PDF [793Кб] и на GraphiCon 2009, PDF [500Кб].
- Вписывание экспериментального среза в построенную трехмерную модель. В настоящее время реализован полуавтоматический метод. Ведется работа над автоматизацией метода.
- Определение уровня экспрессии генов на экспериментальных срезах и построение трехмерной карты экспрессии. Работа ведется в настоящий момент.
- Статистический анализ экспрессии генов с учетом информации об принадлежности определенным анатомическим структурам. Работа ведется в настоящий момент.
Морфинг трехмерной модели мозга:
Множественный трекинг лабораторных животных
Одним из основных инструментов в современных когнитивных исследованиях являются методы анализа поведения человека или животного. Построение описания поведения вручную является очень трудоемким процессом, поэтому все большую популярность получают системы автоматического анализа поведения. Такие системы, как правило, включают в себя модуль видеонаблюдения, модуль сегментации видеосигнала (выделения в нем элементарных структурных единиц поведения — поведенческих актов) и модуль поиска закономерностей в поведении. Первичным элементом любой системы автоматического анализа поведения является модуль видеонаблюдения, позволяющий осуществлять сопровождение наблюдаемого объекта (трекинг) и, возможно, оценивать ряд его характеристик, например, геометрическую форму, скорость и т. п. Наибольшее распространение такие системы получили для наблюдения за лабораторными мышами. Серьезным ограничением современных систем видеонаблюдения за животными является их неспособность осуществлять наблюдение и идентификацию одновременно для нескольких животных, находящихся в клетке. Это сильно ограничивает область их применения, т.к. не позволяет анализировать социальное поведение. Кроме того, большую часть времени вне экспериментов животное проводит в т.н. домашней клетке, содержащей обычно 3–5 мышей. Для изучения изменений поведения животного в течение долгих интервалов времени (недели, месяцы) желательно осуществлять видеонаблюдение за ним и в домашней клетке. Современные технологии позволяют это сделать аппаратно, но надежных методов для множественного трекинга и идентификации мышей в клетке до сих пор не создано. Это связано в первую очередь со сложностями при разделении мышей, которые любят сбиваться в кучку и находиться в тесном телесном контакте, а также с персонификацией найденных особей.
Пример работы алгоритма множественного трекинга:
Определение поведенческих актов животного по данным видеонаблюдения
Необходимость создания высокопроизводительных и экономически эффективных методов поведенческого фенотипирования (скрининга) лабораторных мышей привела к появлению автоматических домашних клеток, предоставляющих исследователям возможность оказывать на мышей различные стимулирующие воздействия, и оборудованные системами видеонаблюдения. Современные же методы анализа поведения, например, выделение поведенческих шаблонов и стереотипии требуют разделения траекторий движения на отдельные поведенческие акты. Эта задача в настоящее время может быть выполнена только с привлечением опытного специалиста в области поведения животных. Существующие системы видеонаблюдения за поведением животных позволяют определять некоторые акты с помощью простейших эвристических метрик, например, сравнивая длину мыши с порогом, что обеспечивает крайне низкую точность распознавания. Автоматические методы сегментации траекторий на данный момент позволяют выделять только периоды двигательной активности и неподвижности, требуют тщательной настройки параметров, что существенно ограничивает их применимость на практике.
Пример сегментации поведения животного:
Нахождение скрытых закономерностей в поведении
Задача поиска поведенческих закономерностей пришла из биологии. Исходными данными для исследования является временной ряд, в каждый момент времени которого может наблюдаться некоторое действие. Задачей является поиск характерных, повторяющихся цепочек действий во времени. Простейшим примером паттерна может служить процесс приема пищи: человек моет руки, после чего, идет на кухню, потом отодвигает стул, садится, берет в руки вилку. Однако исследователей интересуют паттерны, которые человеку сложно, или невозможно выделить с помощью визуального анализа. Такие закономерности принято называть скрытыми(Hidden Time Patterns).
В данной работе, PDF [343Кб] был реализован и модифицирован алгоритм, предложенный М.С.Магнусоном («Discovering hidden time patterns in behavior» M.S.Magnusson 2000, PDF [1MB]). Предложенный метод основывается на опеределении взаимосвязи между парами событий, названной критическим отношением. Поиск производится снизу вверх: алгоритм сначала находит простые закономерности, потом, путем соединения простых, образуются более сложные паттерны. На каждом шаге проводится отбор самых существенных и полных паттернов. Алгоритм был реализован на языке Си в виде консольного приложения и модуля Matlab.
На данный момент разрабатывается графическое приложение, позволяющее анализировать результаты поиска и распределения паттернов.
Анализ изображений клеточных структур
Проблема выделения клеток на изображении не является новой. Все эти задачи успешно решаются с использованием методов свертки, бинаризации и геометрических преобразований. Задача, которая рассматривалась в данной работе, отличается от них тем, что необходимо учитывать и корректно распознавать очень маленькие объекты – почки.
Задача решена с помощью последовательного применения методов, каждый из которых был модифицирован с учетом ее специфики: алгоритм свертки, бинаризация с учетом цветовой компоненты, выделение связных областей, фильтрация и отсеивание шума. Для анализа наличия почек проведены проверки на симметричность и отклонения от выпуклой оболочки. Кроме того, рассмотрены пути обработки сгустков клеток, отнесенных в одну связную область. Итоговый алгоритм допускает на изображениях с общим числом клеток около ста примерно одну-две ошибки первого и второго рода – точность, сравнимая с ручным подсчетом.
Статья с конференции Graphicon 2009, PDF [432Кб]
Краткосрочное прогнозирование солнечной активности
Совместно с коллегами из Microsoft Research решается задача краткосрочного прогнозирования солнечных вспышек, которые вызывают на Земле и на ее орбите магнитные бури. Актуальность задачи заключается в том, что последствия магнитной бури могут носить пагубный характер: вышедшие из строя спутники, помехи связи, сбои в работе электроники. Качественное предсказание аномальной солнечной активности позволит своевременно предпринимать необходимые шаги по минимизации ущерба от подобных событий.
Исходными данными для задачи являются снимки солнечной поверхности со спутника, сделанные в оптическом и магнитном диапазонах. Непосредственным признаком будущей солнечной вспышки является наличие солнечных пятен в оптическом диапазоне и усложненная структура полей на магнитограмме.
Проводимое исследование ставит перед собой несколько целей:
- автоматическое краткосрочное (за 6-12 часов до взрыва) прогнозирование факта солнечной вспышки с указанием времени вспышки и ее силы,
- получение и анализ статистики по вспышкам и пятнам за все доступные для изучения года,
- классификация солнечных пятен по Макинтошу в автоматическом режиме,
- перенесение всех разработок в Интернет (функционирование в режиме 24x7, результаты общедоступны).
Основные этапы работы над проектом:
- алгоритмы препроцессинга (включает в себя и нетривиальные: выравнивание с помощью откалиброванного среднего изображения, сферическая коррекция и др.), сегментации (использована адаптивная бинаризация) и кластеризации солнечных пятен для изображений в оптическом диапазоне,
- сегментация активного региона на магнитограмме с помощью разрезов графов (результаты средние) и вариационного приближения (удачно),
- формирование базы данных вспышек за 1995-2009 гг,
- создание базы изображений за эти года (объем > 300 ГБ),
- расчет предыстории для каждой вспышки из базы (серии и в магнитном, и в оптическом диапазонах), фактически, осуществлен трекинг солнечных пятен/областей магнитной активности во времени,
- выделение признаков из серий изображений, предшествующих вспышке,
- конструирование решающего правила.
Теоретическая работа
Непрерывное обобщение информационного критерия Акаике в задачах регрессии и классификации
Предложен метод отбора признаков для линейной регрессии с помощью обобщения информационного критерия Акаике. Использование классического информационного критерия Акаике (AIC, Akaike Information Criterion) для отбора признаков связано с полным перебором по всем подмножествам признаков, что приводит к неоправданно большим вычислительным и временным затратам. Получен новый информационный критерий CAIC (Continuous Akaike Information Criterion), который является непрерывным обобщением AIC. В результате задача отбора признаков сводится к задаче гладкой оптимизации. Выведена эффективная процедура решения полученной задачи оптимизации. Экспериментальные исследования показывают, что разработанный метод действительно позволяет быстро и эффективно отбирать признаки в линейной регрессии. Проведено сравнение новой процедуры с методом релевантных векторов, который является методом отбора признаков на основе байесовского подхода. Показано, что обе процедуры близки по результатам. Основное отличие нового метода состоит в том, что некоторые коэффициенты регуляризации становятся тождественно равными нулю. Это позволяет избежать эффекта переупрощения модели, который характерен для метода релевантных векторов. Также рассматрен специальный случай (так называемая недиагональная регуляризация), в котором оба метода оказываются идентичными.
Исследовано расширение критерия CAIC на случай представления параметра регуляризации в виде симметричной неотрицательно определенной матрицы. Выведено явное условие вырожденности решающего правила (нулевых весов признаков). Доказана справедливость данного условия для семейства диагональных неотрицательно определенных матриц, а также для семейства матриц, пропорциональных единичной.
Исследована унимодальность критерия для 4-х типов матриц регуляризации:
- Матрица регуляризации – любая симметрическая неотрицательно определенная матрица;
- Матрица регуляризации - симметрическая неотрицательно определенная матрица, являющаяся диагональной в базисе из собственных векторов гессиана логарифма правдоподобия;
- Диагональная матрица регуляризации;
- Матрица регуляризации пропорциональна единичной.
Установлено, что унимодальность имеет место лишь в двух случаях из четырех.
Недиагональная регуляризация обобщенных линейных моделей
Рассмотрен новый тип процедуры регуляризации в Байесовских методах классификации. В основе предлагаемого подхода лежит приведение матрицы гессиана логарифма функции правдоподобия к диагональному виду с последующей независимой регуляризацией вдоль собственных векторов. Это позволяет представить обоснованность (evidence) в виде произведения одномерных интегралов, из-за чего процесс автоматического определения коэффициентов регуляризации сходится за одну итерацию. В качестве примеров показано использование данного подхода для Гауссовского и Лапласовского априорных распределений. В обоих случаях качество полученного решения сравнимо с тем, которое дает метод релевантных векторов RVM (Relevance Vector Machine), при этом время обучения метода меньше, а разреженность решающего правила выше.
Автоматическое определение количества компонент в EM-алгоритме восстановления смеси нормальных распределений
Классический ЕМ-алгоритм восстановления смеси нормальных распределений не позволяет определять количество компонент смеси. В работе предлагается алгоритм автоматического определения числа компонент ARD EM, основанный на методе релевантных векторов. Идея алгоритма состоит в использовании на начальном этапе заведомо избыточного количества компонент смеси с дальнейшим определением релевантных компонент с помощью максимизации обоснованности. Эксперименты на модельных задачах показывают, что количество найденных кластеров либо совпадает с истинным, либо немного превосходит его. Кроме того, кластеризация с помощью ARD EM оказывается ближе к истинной, чем у аналогов, основанных на скользящем контроле и принципе минимальной длины описания.
См. также
EM-алгоритм с последовательным добавлением компонент
Вариационный метод релевантных векторов для задач классификации и регрессии с многомерными векторами признаков
Рассматриваются задачи классификации и восстановления регрессии, в которых объекты представлены многомерными массивами. К задачам такого вида сводятся многие практические постановки, например, часто используемый в анализе изображений подход к описанию изображений в виде набора блоков и набора дескрипторов в каждом блоке, или описание объекта как набор расстояний от этого объекта до некоторого количества опорных объектов, взятых по некоторому набору исходных признаков. Для решения задач с такими объектами предложено обобщение модели релевантных векторов. Здесь свои коэффициенты регуляризации вводятся для каждой размерности многомерного массива описаний объектов, а итоговый коэффициент регуляризации для заданного элемента в многомерном массиве определяется как комбинация коэффициентов регуляризации для всех размерностей. В качестве комбинаций рассмотрены модели с суммой и произведением. Для обучения в этих моделях предложены алгоритмы на основе вариационного подхода. Эти алгоритмы позволяют находить т.н. «разреженные» решения, т.е. исключать из рассмотрения нерелевантные размерности в многомерном массиве описаний объектов. По сравнению с классической моделью релевантных векторов в предлагаемом подходе происходит сокращение количества настраиваемых параметров: вместо произведения всех размерностей рассматривается сумма. В результате метод становится менее чувствительным к переобучению на выборках с небольшим числом объектов. Последнее свойство, а также разреженность получаемых решений в предлагаемых моделях продемонстрировано в экспериментах, в том числе для известной базы данных по идентификации лиц в произвольных условиях Labeled Faces in the Wild.
Статья (PDF)
Реализация для MatLab доступна здесь.
Композитно-иерархические скрытые марковские модели
Сегментация изображений с учетом априорной информации о площади сегментов
Рассматривается задача сегментации изображений на несколько классов с учетом априорной информации о площади сегментов. Данная задача решается в два этапа: использование вариационного приближения для определения вероятности принадлежности пикселей изображения каждому из классов, а затем построение оптимальной конфигурации с учетом априорной информации при помощи решения транспортной задачи.
Алгоритм с небольшими изменениями позволяет решать задачи с несколькими типами априорной информации о площади сегментов:
1. жесткие ограничения в виде равенства на площадь каждого сегмента,
2. ограничения в виде интервала, которому должна принадлежать площадь каждого сегмента,
3. распределение Лапласа на площади сегментов,
4. нормальное распределение на площади сегментов.
Пример работы алгоритма с жесткими ограничениями можно посмотреть в приложенных изображениях: левое изображение - оригинальное, по центру - сегментация без ограничений на площадь сегментов (отнесение каждого пикселя к наиболее вероятному классу), правое - с ограничениями в виде равенства (относительно наиболее вероятной разметки уменьшена площадь "желтого" и "синего" класса в пользу "голубого").
См. также
- Англоязычная страница группы Байесовских методов
- Спецкурс «Байесовские методы машинного обучения»
- Курс «Графические модели»
- Спецкурс «Методы оптимизации в машинном обучении»
- Байесовские методы машинного обучения (Спецсеминар)/2010-2011