Статистический анализ данных (курс лекций, К.В.Воронцов)/2011
Материал из MachineLearning.
Задание 1. Исследование свойств одномерных статистических критериев на модельных данных
Необходимо провести исследование одного или нескольких классических критериев проверки статистических гипотез. Интерес представляет поведение достигаемого уровня значимости (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо указанным способом сгенерировать одну или несколько выборок из заданного распределения, выполнить проверку гипотезы при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. По результатам расчётов необходимо построить требуемые в задании графики, среди которых могут быть следующие:
- график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента;
- график зависимости достигаемого уровня значимости одного или двух критериев от значений параметров, усреднённого по большому количеству повторений эксперимента (например, по 1000 повторений);
- график с эмпирическими оценками мощности одного или двух критериев для разных значений параметров.
В качестве оценки мощности принимается доля отвержений нулевой гипотезы среди всех проверок. То есть, если эксперимент повторялся раз для каждого набора значений параметров, и в
из
случаев гипотеза была отвергнута на некотором фиксированном уровне значимости
(примем
), оценкой мощности будет отношение
Необходимо сдать: выполненный в LaTex или Microsoft Word отчёт с описанием алгоритма, построенными графиками и выводами (объяснение полученных результатов моделирования, границы применимости критерия и т.д.), а также *.m-файл или R-скрипт, при запуске которого на экран выводятся графики, соответствующие имеющимся в отчёте.
Задание принимается до первого ноября.
Пример задания
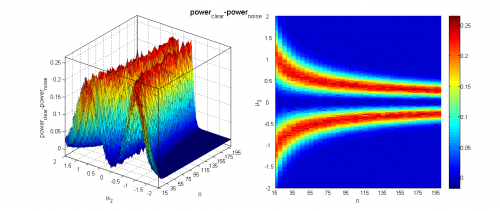
Исследуем чувствительность классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига при зашумлении выборок наблюдениями, взятыми из равномерного распределения.
— выборка длины
из смеси стандартного нормального
и равномерного
распределений с весами
и
соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит
, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
— аналогичная выборка.
При каждом значении выборки для разных значений
генерируются независимо.
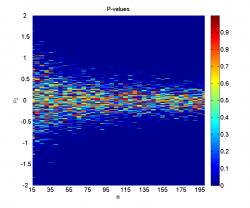
Заметим, что однократная генерация выборок даёт достаточно нестабильные результаты, не позволяя точно оценить границы области, где нулевая гипотеза отклоняется, поэтому и необходимо усреднение по большому числу экспериментов.
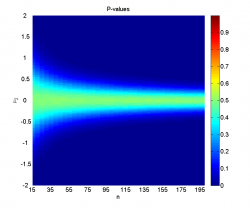
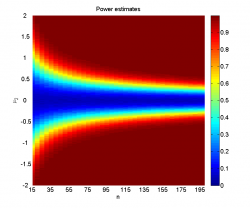
Видно, что при достаточно большой разнице между средними и большом размере выборок наличие шума не мешает уверенно отклонять гипотезу однородности. Когда, наоборот, разница между средними невелика (меньше 0.2-0.5 в зависимости от размера выборок), мощность близка к нулю, а среднее значение достигаемого уровня значимости колеблется около 0.5, что логично, так как его распределение при справедливости нулевой гипотезы равномерно на .
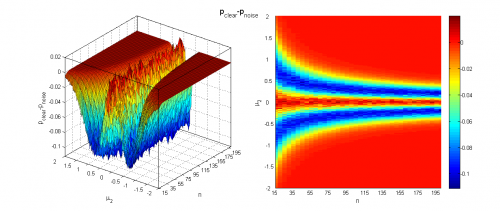
Чтобы оценить вклад зашумления выборок, оценим при всех значениях параметра мощность критерия и средний достигаемый уровень значимости на аналогичных выборках без шума и сравним результаты.
Видно, что наличие шума всё меньше влияет на работу критерия с ростом объёма выборок и разницы между их средними. Тем не менее, в некоторых областях изменения параметров потеря мощности из-за 10% зашумления может составлять до 20%, а средний достигаемый уровень значимости может быть выше на 0.1.
Отметим, что приведённые количественные выводы справедливы только для шума рассматриваемой структуры.
Задания
Анализ чувствительности критериев к редактированию выборки
Известно, что исключение из выборки определённых наблюдений зачастую может достаточно сильно повлиять на результат анализа. Необходимо исследовать чувствительность указанного критерия к редактированию выборки, построить графики, сделать выводы.
На каждом шаге генерируются выборки исходной длины, проводится проверка гипотезы , затем по некоторому правилу из указанной выборки исключается один из элементов, проверка гипотезы повторяется, затем исключается ещё один, и т.д. Обозначим за
максимальное число исключённых в таком процессе элементов; примем во всех задачах
.
- Двухвыборочный критерий Стьюдента для связных выборок.
- Алешина Мария:
на каждом шаге исключается пара наблюдений
разность которых максимальна.
- Антипов Григорий:
на каждом шаге исключается пара наблюдений
разность которых минимальна.
- Алешина Мария:
- Критерий Уилкоксона-Манна-Уитни для независимых выборок.
- Батурина Вера:
на каждом шаге исключается максимальный элемент выборки
.
- Бондаренко Николай:
на каждом шаге исключается максимальный элемент выборки
.
- Валов Дмитрий:
на каждом шаге исключается минимальный элемент выборки
.
- Батурина Вера:
- Критерий Фишера для проверки равенства дисперсий.
- Головин Антон:
на каждом шаге исключается максимальный по модулю элемент выборки
.
- Дударенко Мария:
на каждом шаге исключается минимальный по модулю элемент выборки
.
- Исупова Ольга:
на каждом шаге исключается максимальный элемент выборки
.
- Касперский Иван:
на каждом шаге исключается минимальный элемент выборки
.
- Головин Антон:
Устойчивость критериев к нарушению предположения нормальности
Исследовать поведение параметрических критериев, предполагающих нормальность данных, при зашумлении выборок наблюдениями, взятыми из равномерного распределения.
- Двухвыборочный критерий Стьюдента для связных выборок
— связанная с ней выборка, полученная добавлением компоненты
из смеси нормального
и равномерного
распределений с весами
и
соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит
, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного),
- Колев Денис:
- Колесников Александр:
- Макарова Елена:
- Колев Денис:
- Критерий Фишера для проверки равенства дисперсий.
— выборка длины
из смеси нормального
и равномерного
распределений с весами
и
соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит
, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного),
— аналогичная выборка,
- Миняйлов Владимир:
- Молчанов Андрей:
- Онищенко Алина:
- Миняйлов Владимир:
Анализ поведения разновидностей критерия Стьюдента
Критерий Стьюдента может явно учитывать дополнительную информацию о дисперсии выборок и их структуре. Необходимо исследовать, какой выигрыш даёт эта информация, сравнив мощности и средние достигаемые уровни значимости вариантов критериев при различных значениях параметров.
- Парный критерий Стьюдента и версия для независимых выборок и неизвестных неравных дисперсий.
- Платонова Елена:
- Семенов Олег:
- Платонова Елена:
- Критерий Стьюдента для независимых выборок, версии для неизвестных и известных неравных дисперсий.
- Сидоров Юрий:
- Солодкин Дмитрий:
- Сидоров Юрий:
- Парный критерий Стьюдента и версия для независимых выборок и известных неравных дисперсий.
(cогласно свойствам нормального распределения, .)
- Суворов Михаил:
- Тихонов Андрей:
- Суворов Михаил:
Задание 2. Анализ реальных данных
Ниже приведены описания анализируемых данных и постановки задач. Сами данные каждый студент может получить по электронной почте после сдачи первого задания. При проведении анализа можно пользоваться любыми доступными программными средствами. Необходимо предоставить подробный письменный отчёт по проведённому исследованию, содержащий выводы и описания каждого этапа анализа — используемые методы, обоснование их применимости, промежуточные результаты вычислений, графики. Помимо выводов, касающихся математических особенностей решения, необходимо включить в отчёт заключения, сформулированные в терминах предметной области, которые могли бы быть понятны гипотетическому заказчику-нематематику.
Cдача задания является необходимым условием получения допуска к экзамену — студенты, не получившие зачёт к моменту сдачи экзамена, не смогут его сдавать, и должны будут выполнить задание к пересдаче.
Относительная минеральная плотность позвоночника
У 261 испытуемых в возрасте от 5 до 26 лет от одного до трёх раз была измерена относительная минеральная плотность позвоночника; всего имеется 485 измерений. Приведены также данные о поле каждого испытуемого.
- Семенов Олег: построить функцию, предсказывающую относительную минеральную плотность позвоночника по полу и возрасту.
- Алешина Мария: проанализировать различия по относительной минеральной плотности между испытуемыми мужского и женского пола, исключив возможное влияние возраста.
- Дударенко Мария: исследовать различия между испытуемыми, для которых имеется только одно, два или три измерения.
Вкус и химический состав сыра чеддер
30 разновидностей сыра чеддер было проанализировано как с точки зрения химического состава, так и с помощью дегустаторов. Для каждой разновидности известны: оценка вкуса, полученная путём усреднения оценок, выставленных несколькими дегустаторами, логарифмы концентраций уксусной кислоты и сульфида водорода, концентрация молочной кислоты.
- Онищенко Алина: построить функцию, по химическому составу сыра предсказывающую его оценку дегустаторами и границы доверительного интервала для неё.
- Валов Дмитрий: построить функцию, позволяющую по оценке вкуса и логарифмам концентраций уксусной кислоты и сульфида водорода восстанавливать концентрацию молочной кислоты.
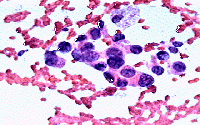
Клетки опухолей груди
357 испытуемым с доброкачественными и 212 со злокачественными опухолями груди была сделана тонкоигольная аспирационная пункция с гистологическим исследованием пунктата. По полученным изображениям определялись следующие признаки опухолевых клеток: радиус, однородность текстуры, периметр, площадь, гладкость, компактность, степень вогнутости, доля вогнутых участков контура, симметричность, фрактальная размерность. Для каждого изображения были рассчитаны среднее значение каждого из этих признаков, стандартное отклонение и среднее по трём клеткам с максимальным значением признака.
- Касперский Иван: оценить вероятность того, что опухоль злокачественная, по набору рассчитанных по изображению признаков. Построить функции, дающие точечную оценку и границы 95% доверительного интервала.
Пассажиры Титаника
Приведены данные о 1309 пассажирах Титаника. Для каждого пассажира указано имя, пол, возраст, класс и цена билета, число родственников на борту, и, кроме того, удалось ли ему выжить.
- Головин Антон: по каким признакам отличаются выжившие пассажиры от погибших?
- Исупова Ольга: построить функции, предсказывающие вероятность выживания пассажира по имеющимся данным и границы доверительного интервала для неё.
Концентрация озона
Имеются данные измерений состояния атмосферы, произведённых в Нью-Йорке в течение 111 подряд идущих дней. Измерены температура воздуха, скорость ветра, уровень солнечной радиации и концентрация озона.
- Антипов Григорий: построить прогноз состояния атмосферы на следующие 10 дней.
- Колев Денис: построить функцию, по имеющимся признакам оценивающую наиболее вероятное значение концентрации озона и доверительный интервал для него.
- Платонова Елена: построить функцию, по имеющимся признакам оценивающую наиболее вероятное значение уровня солнечной радиации и доверительный интервал для него.
Солнечная активность
В центре исследования солнечной активности Цюрихской обсерватории собраны данные о среднем числе солнечных пятен за каждый месяц с января 1749 года.
- Батурина Вера: предсказать среднее число солнечных пятен на каждый месяц до конца 2020 года.
Стоимость подержанных автомобилей
Имеются данные о стоимости 804 подержанных автомобилей и их характеристиках: известны пробег, производитель, модель, вид модели, тип кузова, число цилиндров, объём двигателя, число дверей, а также наличие или отсутствие круиз контроля, продвинутой звуковой системы и кожаной обивки сидений.
- Бондаренко Николай: построить модель стоимости автомобиля по данному набору признаков.
- Колесников Александр: исследовать взаимосвязи между признаками, сравнить распределения признаков в группах, образуемых разбиениями по дискретным признакам.
Продолжительность жизни и активность размножения самцов дрозофилы
Для изучения влияния активности размножения самцов дрозофилы на продолжительность их жизни был организован следующий эксперимент. По 25 самцов в пяти группах содержались в одинаковых условиях, за исключением одного отличия: в первой группе к каждому самцу ежедневно подсаживалась готовая к размножению самка, во второй – восемь готовых к размножению самок, в третьей и четвёртой - соответственно, одна и восемь беременных самок, не готовых к размножению, наконец, к самцам четвёртой группы не подсаживали никого. Для каждого самца измерена продолжительность жизни, длина грудной клетки и доля времени, проводимого во сне.
- Суворов Михаил: сравнить продолжительность жизни самцов в разных группах.
- Тихонов Андрей: построить функцию, предсказывающую продолжительность жизни самца дрозофилы в зависимости от условий его содержания.
Массовая доля жира в организме
Массовая доля жира, важная характеристика здоровья, рассчитывается через плотность тела, измеряемую при помощи взвешивания в воде. Для 252 мужчин проведены такие расчёты. Имеются также данные антропометрии (возраст, рост, вес, обхват грудной клетки и т.д.)
- Миняйлов Владимир: построить функцию, оценивающую массовую долю жира по легко измеряемым антропометрическим признакам.
- Молчанов Андрей: построить функцию, оценивающую индекс ожирения без использования данных взвешивания.
Диета цыплят
Для 50 цыплят, разбитых на 4 группы по типу диеты, имеются результаты взвешивания в возрасте от 0 до 21 дней; пропущенные значения соответствуют умершим цыплятам.
- Макарова Елена: сравнить эффективность различных типов диеты.
Литература
Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006.