Критерий Бартлетта
Материал из MachineLearning.
| Строка 1: | Строка 1: | ||
| - | '''Критерий Бартлета''' позволяет проверять равенство дисперсий нескольких выборок. При этом объемы выборок могут быть различными. | + | '''Критерий Бартлета''' позволяет проверять равенство дисперсий нескольких выборок. При этом объемы выборок могут быть различными. Критерий Бартлетта очень чувствителен к нарушению предположения о нормальности. |
| + | |||
== Описание критерия == | == Описание критерия == | ||
| - | + | Имеется <tex>k</tex> выборок <tex>x^{n_1}_1, . . . , x^{n_k}_k</tex> объемом <tex>n_i</tex> (<tex>i=1,...,k </tex>) каждая. Дисперсии выборок и выборочные оценки дисперсий обозначим через <tex>\sigma_i^2</tex> и <tex>s_i^2</tex> соответственно. | |
| - | <tex>x^{n_1}_1,...,x^{n_k}_k</tex>, | + | |
| + | === Дополнительные предположения === | ||
| + | * ''Выборки <tex>x^{n_1}_1, . . . , x^{n_k}_k</tex> являются нормальными''. Критерий Бартлетта очень чувствителен к отклонениям от нормальности распределения исследуемых случайных величин. Если нет уверенности в нормальности распределения, им не рекомендуется пользоваться. | ||
| + | |||
| + | === Нулевая гипотеза === | ||
| + | Критерий Бартлетта проверяет '''гипотезу <tex>H_0</tex>''' о том, что дисперсии всех <tex>k</tex> выборок одинаковы. | ||
| + | ::<tex>H_0: \sigma_1^2 = \sigma_2^2 = . . . = \sigma_k^2</tex> | ||
| + | Альтернативная '''гипотеза <tex>H_1</tex>''': существует, по крайней мере, две выборки <tex>i</tex> и <tex>j</tex> (<tex>i \neq j</tex>) с несовпадающими дисперсиями. | ||
| + | ::<tex>H_1: \sigma_i^2 \neq \sigma_j^2</tex> (для некоторых <tex>i \neq j</tex>). | ||
| + | |||
| + | |||
| + | === Статистика критерия Бартлетта === | ||
| + | Статистика критерия Бартлетта вычисляется в соответствии с соотношением: | ||
| + | ::<tex>T = \frac{M}{c}</tex>. | ||
| + | Здесь | ||
| + | ::<tex>M = (N-k) \cdot \ln(s^2_p) - \sum_{i=1}^k (n_i - 1) \cdot \ln(s^2_i)</tex>, | ||
| + | ::<tex>c = 1 + \frac{1}{3\cdot (k-1)} \cdot \left(\sum_{i=1}^k \left(\frac{1}{n_i-1} \right) - \frac{1}{(N-k)} \right)</tex>, | ||
| + | где <tex>N = \sum_{i=1}^k n_i </tex> и <tex> s^2_p = \frac{1}{ N-k } \sum_{i=1}^k (n_i - 1) \cdot s^2_i </tex> – суммарная оценка дисперсий. | ||
| + | |||
| + | При <tex>n_i > 3 (i=1,...,k) </tex> и справедливости нулевой гипотезы статистика критерия Бартлетта имеет распределение <tex>\chi_{k-1}^2</tex> хи-квадрат с (k-1) степенями свободы. | ||
| + | |||
| + | === Критерий (при уровне значимости <tex> \alpha</tex>) === | ||
| + | Если <tex> T > \chi_{k-1, \alpha}^2</tex>, то с достоверностью <tex> \alpha</tex> нулевая гипотеза <tex>H_0</tex> ''отвергается'' в пользу альтернативы <tex>H_1</tex>. | ||
| + | |||
| + | === Примечание === | ||
| + | При отклонении от нормальности рекомендуется вместо статистики <tex>T</tex> пользоваться ее модификацией: | ||
| + | ::<tex>T^* = \frac{f_2 \cdot M}{f_1 \cdot \left(\frac{f_2^2}{f_2 (2-c) + c} - M \right)}</tex>, | ||
| + | где <tex>f_1 = k-1</tex>, <tex>f_2 = \frac{k+1}{(c-1)^2}</tex>. | ||
| + | |||
| + | Статистика <tex> T^*</tex> имеет <tex>F</tex>-распределение с <tex>f_1</tex> и <tex>f_2</tex> степенями свободы. Поэтому нулевую гипотезу следует отклонить, если <tex>T^* > F_{\alpha}(f_1, f_2)</tex>. | ||
== Литература == | == Литература == | ||
| + | # {{книга | ||
| + | |автор = Кобзарь А. И. | ||
| + | |заглавие = Прикладная математическая статистика | ||
| + | |издательство = М.: Физматлит | ||
| + | |год = 2006 | ||
| + | |страниц = 816 | ||
| + | }} | ||
== См. также == | == См. также == | ||
| Строка 13: | Строка 50: | ||
== Ссылки == | == Ссылки == | ||
* [http://en.wikipedia.org/wiki/Bartlett's_test Bartlett's test] (Wikipedia) | * [http://en.wikipedia.org/wiki/Bartlett's_test Bartlett's test] (Wikipedia) | ||
| - | + | * [http://www.itl.nist.gov/div898/handbook/eda/section3/eda357.htm NIST page on Bartlett's test] | |
| - | + | ||
[[Категория: Прикладная статистика]] | [[Категория: Прикладная статистика]] | ||
Версия 21:15, 5 января 2009
Критерий Бартлета позволяет проверять равенство дисперсий нескольких выборок. При этом объемы выборок могут быть различными. Критерий Бартлетта очень чувствителен к нарушению предположения о нормальности.
Содержание |
Описание критерия
Имеется выборок
объемом
(
) каждая. Дисперсии выборок и выборочные оценки дисперсий обозначим через
и
соответственно.
Дополнительные предположения
- Выборки
являются нормальными. Критерий Бартлетта очень чувствителен к отклонениям от нормальности распределения исследуемых случайных величин. Если нет уверенности в нормальности распределения, им не рекомендуется пользоваться.
Нулевая гипотеза
Критерий Бартлетта проверяет гипотезу о том, что дисперсии всех
выборок одинаковы.
Альтернативная гипотеза : существует, по крайней мере, две выборки
и
(
) с несовпадающими дисперсиями.
(для некоторых
).
Статистика критерия Бартлетта
Статистика критерия Бартлетта вычисляется в соответствии с соотношением:
.
Здесь
,
,
где и
– суммарная оценка дисперсий.
При и справедливости нулевой гипотезы статистика критерия Бартлетта имеет распределение
хи-квадрат с (k-1) степенями свободы.
Критерий (при уровне значимости 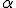 )
)
Если , то с достоверностью
нулевая гипотеза
отвергается в пользу альтернативы
.
Примечание
При отклонении от нормальности рекомендуется вместо статистики пользоваться ее модификацией:
,
где ,
.
Статистика имеет
-распределение с
и
степенями свободы. Поэтому нулевую гипотезу следует отклонить, если
.
Литература
- Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006. — 816 с.
См. также
Ссылки
- Bartlett's test (Wikipedia)
- NIST page on Bartlett's test

