Статистический анализ данных (курс лекций, К.В.Воронцов)/2009

Материал из MachineLearning.

(Различия между версиями)

Версия 23:04, 13 ноября 2009

Содержание

1 Задание 1. Исследование статистических критериев на модельных данных
- 1.1 Пример выполнения задания
- 1.2 Индивидуальные параметры задания
2 Задание 2. Анализ реальных данных
3 Задание 3. Написание или доработка wiki-статей
- 3.1 Статьи, нуждающиеся в доработке
- 3.2 Новые статьи

Задание 1. Исследование статистических критериев на модельных данных

Необходимо провести исследование одного из классических критериев проверки статистических гипотез. Интерес представляет поведение достигаемого уровня значимости (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо сгенерировать одну или несколько выборок из указанного распределения, выполнить проверку гипотезы при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. При этом, в зависимости от индивидуальных особенностей задания, выборки могут как генерироваться заново для каждого значения объёма выборки $n$ , так и образовываться путём добавления одного элемента к уже имеющейся выборке объёма $n-1$ . По результатам расчётов необходимо построить следующие графики:

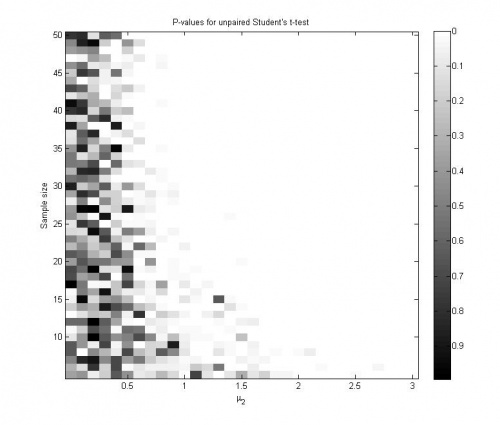
график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента (1 балл);
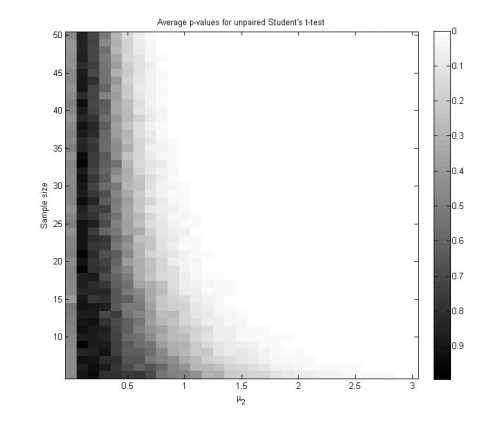
график зависимости достигаемого уровня значимости от значений параметров, усреднённого по нескольким десяткам экспериментов (+1 балл);
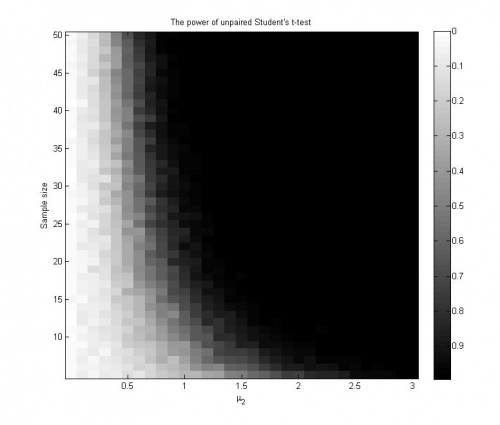
график с эмпирическими оценками мощности критерия для разных значений параметров (+1 балл).

В качестве оценки мощности принимается доля отвержений нулевой гипотезы среди всех проверок. То есть, если эксперимент повторялся $k$ раз для каждого набора значений параметра, и в $m$ из $k$ случаев гипотеза была отвергнута на некотором фиксированном уровне значимости $\alpha$ (примем $\alpha=0.05$ ), оценкой мощности будет отношение $m/k$ .

Необходимо сдать: выполненный в LaTex или Microsoft Word отчёт с описанием алгоритма, построенными графиками и выводами, *.m-файл.

Пример выполнения задания

Исследуем поведение классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига. $x^n = (x_1,\ldots,x_n)\sim N(\mu_1,\sigma),\;\; y^n = (y_1,\ldots,y_n)\sim N(\mu_2,\sigma);$

$H_0\,:\; \mu_1=\mu_2,$

$H_1\,:\; \mu_1\neq\mu_2.$

Параметры задачи принимают следующие значения:

$\sigma = 1; \;\;\; \mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\; n=5\,:\,1\,:\,50.$

При каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

График значений достигаемого уровня значимости при однократной генерации выборок:

График значений достигаемого уровня значимости, усрёднённых по 100 экспериментам:

График значений эмпирических оценок мощности критерия при проведении 100 экспериментов:

Индивидуальные параметры задания

Одновыборочный критерий Стьюдента

$x^n \sim N(\mu,1);$

$H_0\,:\; \mu=0, \;\; H_1\,:\; \mu\neq 0;$

$\mu=0\,:\,0,05\,:\,3; \;\;\; n=5\,:\,1\,:\,50.$

Безродный Богдан

При каждом значении $\mu$ выборки для разных значений $n$ генерируются независимо.

Двойнев Александр

При каждом значении $\mu$ выборка $x^n$ получается из $x^{n-1}$ добавлением одного случайного элемента.

Двухвыборочный критерий Стьюдента для независимых выборок

$x^n \sim N(\mu_1,\sigma_1),\;\; y^n \sim N(\mu_2,\sigma_2);$

$H_0\,:\; \mu_1=\mu_2, \;\; H_1\,:\; \mu_1\neq\mu_2;$

$n=5\,:\,1\,:\,50.$

Коликова Екатерина

$\mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\; \sigma_1=\sigma_2=1;$ при каждом значении $\mu_2$ выборки $x^n, y^n$ получаются из $x^{n-1}, y^{n-1}$ добавлением одного случайного элемента.

Черняев Константин

$\mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\; \sigma_1=\sigma_2=1;$ при каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Задонский Дмитрий

$\mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\; \sigma_1=1;\;\;\sigma_2=2;$ при каждом значении $\mu_2$ выборки $x^n, y^n$ получаются из $x^{n-1}, y^{n-1}$ добавлением одного случайного элемента.

Ломакин Василий

$\mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\; \sigma_1=1;\;\;\sigma_2=2;$ при каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Гуков Алексей

$\mu_1=\mu_2=0; \;\;\; \sigma_1=1;\;\;\sigma_2=0.1\,:\,0.1\,:\,4;$ при каждом значении $\sigma_2$ выборки $x^n, y^n$ получаются из $x^{n-1}, y^{n-1}$ добавлением одного случайного элемента.

Решетняк Илья

$\mu_1=\mu_2=0; \;\;\; \sigma_1=1;\;\;\sigma_2=0.1\,:\,0.1\,:\,4;$ при каждом значении $\sigma_2$ выборки для разных значений $n$ генерируются независимо.

Двухвыборочный критерий Стьюдента для связных выборок (случай парных повторных наблюдений)

$x^n \sim N(\mu_1,1),\;\; y^n \sim N(\mu_2,1);$

$H_0\,:\; \mu_1=\mu_2, \;\; H_1\,:\; \mu_1\neq\mu_2;$

$\mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\; n=5\,:\,1\,:\,50.$

Дзыба Дмитрий

При каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Осокин Антон

При каждом значении $\mu_2$ выборки $x^n, y^n$ получаются из $x^{n-1}, y^{n-1}$ добавлением одного случайного элемента.

Одновыборочный критерий Уилкоксона

$x^n \sim F(\mu);$

$H_0\,:\; \mu=0, \;\; H_1\,:\; \mu\neq 0;$

$\mu=0\,:\,0,05\,:\,3; \;\;\; n=5\,:\,1\,:\,50.$

Задонский Максим

$F(\mu)=N(\mu,1);$ при каждом значении $\mu$ выборки для разных значений $n$ генерируются независимо.

Карпинская Алина

$F(\mu)=N(\mu,1);$ при каждом значении $\mu$ выборка $x^n$ получается из $x^{n-1}$ добавлением одного случайного элемента.

Нарышкин Андрей

$F(\mu)=U[\mu-3,\mu];$ при каждом значении $\mu$ выборки для разных значений $n$ генерируются независимо.

Вишняков Святослав

$F(\mu)=U[\mu-3,\mu];$ при каждом значении $\mu$ выборка $x^n$ получается из $x^{n-1}$ добавлением одного случайного элемента.

Двухвыборочный критерий Уилкоксона для связных выборок (случай парных повторных наблюдений)

$x^n \sim F(\mu_1),\;\; y^n \sim F(\mu_2);$

$H_0\,:\; \mu_1=\mu_2, \;\; H_1\,:\; \mu_1\neq\mu_2;$

$\mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\; n=5\,:\,1\,:\,50.$

Гикал Александр

$F=N(\mu,1);$ при каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Ломакина-Румянцева Екатерина

$F=N(\mu,1);$ при каждом значении $\mu_2$ выборки $x^n, y^n$ получаются из $x^{n-1}, y^{n-1}$ добавлением одного случайного элемента.

Джумабекова Айнагуль

$F=U[0,\mu+1];$ при каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Мягков Артем

$F=U[0,\mu+1];$ при каждом значении $\mu_2$ выборки $x^n, y^n$ получаются из $x^{n-1}, y^{n-1}$ добавлением одного случайного элемента.

Критерий Краскелла-Уоллиса для независимых выборок

$x^n \sim F(\mu_1),\;\; y^n \sim F(\mu_2);$

$H_0\,:\; \mu_1=\mu_2, \;\; H_1\,:\; \mu_1\neq\mu_2;$

$\mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\; n=5\,:\,1\,:\,50.$

Ахламченкова Ольга

$F=N(\mu,1);$ при каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Голодов Валентин

$F=U[0,\mu+1];$ при каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Алимбаев Данияр

Критерий Колмогорова-Смирнова для проверки нормальности

$x^n$ - смесь распределений $N(0,1)$ и $U[-\mu,\mu]$ с весами $\alpha$ и $1-\alpha$ соответственно. При генерации выборки используется случайный датчик - если его значение не превосходит $\alpha$ , то добавляем в выборку элемент, взятый из нормального распределения, иначе - элемент, взятый из равномерного;

$H_0\,:\; x^n\sim \cdot N(0,1), \;\; H_1\,:\; F_n(x)\neq N(0,1);$

$\alpha=0\,:\,0,02\,:\,1; \;\;\; n=10\,:\,5\,:\,250.$

При каждом значении параметров выборки для разных значений $n$ генерируются независимо.

Толстихин Илья

$\mu=1.$

Янгиров Ильдар

$\mu=2.$

Критерий хи-квадрат Пирсона для проверки нормальности

$H_0\,:\; x^n\sim \cdot N(0,1), \;\; H_1\,:\; F_n(x)\neq N(0,1);$

$\alpha=0\,:\,0,02\,:\,1; \;\;\; n=10\,:\,5\,:\,250.$

При каждом значении параметров выборки для разных значений $n$ генерируются независимо.

Дерябин Василий

$\mu=1.$

Одинокова Евгения

$\mu=2.$

F-критерий Фишера для проверки равенства дисперсий

$x^n \sim N(0,\sigma_1),\;\; y^n \sim N(\mu,\sigma_2);$

$H_0\,:\; \sigma_1=\sigma_2, \;\; H_1\,:\; \sigma_1\neq \sigma_2;$

$n=5\,:\,1\,:\,50.$

Аманжолов Рустем

$\mu=0; \;\;\; \sigma_1=1, \;\; \sigma_2=0.1\,:\,0.1\,:\,4;$ при каждом значении $\sigma_2$ выборки для разных значений $n$ генерируются независимо.

Пасконова Ольга

$\mu=0; \;\;\; \sigma_1=1, \;\; \sigma_2=0.1\,:\,0.1\,:\,4;$ при каждом значении $\sigma_2$ выборки $x^n, y^n$ получаются из $x^{n-1}, y^{n-1}$ добавлением одного случайного элемента.

Гордеев Дмитрий

$\sigma_1=\sigma_2=1; \;\;\; \mu=0\,:\,0,05\,:\,3;$ при каждом значении $\mu$ выборки для разных значений $n$ генерируются независимо.

Найденов Никита

$\sigma_1=\sigma_2=1; \;\;\; \mu=0\,:\,0,05\,:\,3;$ при каждом значении $\mu$ выборки $x^n, y^n$ получаются из $x^{n-1}, y^{n-1}$ добавлением одного случайного элемента.

Задание 2. Анализ реальных данных

Ниже приведены описания анализируемых данных и постановки задач. Сами данные каждый студент может получить по электронной почте сразу после сдачи первого задания.

Интеллект и размер головного мозга

Исследование проводилось среди студентов психологического факультета крупного университета. Все испытуемые должны были быть правшами, а также не иметь повреждений мозга, эпилепсии, алкоголизма и сердечных заболеваний. Участники предварительного этапа эксперимента прошли несколько IQ-тестов, после чего для дальнейшего участия было отобрано 20 мужчин и 20 женщин, имевших коэффециент интеллекта от 103 до 130 баллов. Для каждого из них при помощи магнитно-резонансной томографии были получены 18 снимков срезов головного мозга, и общее количество пикселей на всех 18 снимках было принято в качестве меры объёма мозга. Помимо этого, были собраны данные о росте и массе тела испытуемых.

Толстихин Илья

Проверить наличие взаимосвязи между интеллектом и объёмом головного мозга для всех испытуемых, независимо от пола, затем провести аналогичный анализ отдельно для мужчин и женщин. Исследовать ту же зависимость, исключив влияние факторов роста и массы тела.

Осокин Антон

Проанализировать, какие из факторов значимо влияют на объём головного мозга. Проверить, по какой из двух групп факторов можно предсказывать объём головного мозга с большей уверенностью - по результатам тестов интеллекта, или по полу, росту и весу.

Продолжительность жизни больных онкологическими заболеваниями

Выборка состоит из 64 пациентов, у которых был диагностирован неизлечимый рак какого-либо органа. Всем им в качестве поддерживающей терапии был назначен к приёму витамин C (считалось, что он может способствовать выздоровлению раковых больных). Приведены данные об остаточной продолжительности жизни пациентов в днях.