Критерий Бартлетта
Материал из MachineLearning.
м («Критерий Бартлета» переименована в «Критерий Бартлетта»: исправление) |
Версия 07:44, 11 января 2009
Критерий Бартлета позволяет проверять равенство дисперсий нескольких выборок. При этом объемы выборок могут быть различными. Критерий Бартлетта очень чувствителен к нарушению предположения о нормальности.
Содержание |
Описание критерия
Имеется выборок
объемом
(
) каждая. Дисперсии выборок и выборочные оценки дисперсий обозначим через
и
соответственно.
Дополнительные предположения
- Выборки
являются нормальными. Критерий Бартлетта очень чувствителен к отклонениям от нормальности распределения исследуемых случайных величин. Если нет уверенности в нормальности распределения, им не рекомендуется пользоваться.
Нулевая гипотеза
Критерий Бартлетта проверяет гипотезу о том, что дисперсии всех
выборок одинаковы.
Альтернативная гипотеза : существует, по крайней мере, две выборки
и
(
) с несовпадающими дисперсиями.
(для некоторых
).
Статистика критерия Бартлетта
Статистика критерия Бартлетта вычисляется в соответствии с соотношением:
.
Здесь
,
,
где и
– суммарная оценка дисперсий.
При и справедливости нулевой гипотезы статистика критерия Бартлетта имеет распределение
хи-квадрат с (k-1) степенями свободы.
Критерий (при уровне значимости 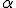 )
)
Если , то с достоверностью
нулевая гипотеза
отвергается в пользу альтернативы
.
Примечание
При отклонении от нормальности рекомендуется вместо статистики пользоваться ее модификацией:
,
где ,
.
Статистика имеет
-распределение с
и
степенями свободы. Поэтому нулевую гипотезу следует отклонить, если
.
Литература
- Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006. — 816 с.
См. также
Ссылки
- Bartlett's test (Wikipedia)
- NIST page on Bartlett's test

