Порождение линейных регрессионных моделей (постановка задачи)
Материал из MachineLearning.
Рассмотрим задачу восстановления линейной регрессии одной свободной переменной.
Содержание |
Дано
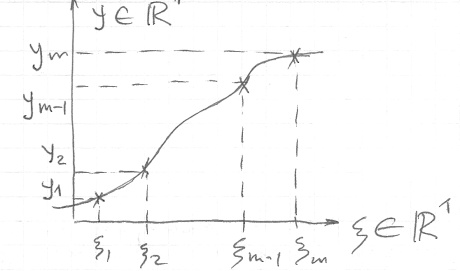
Задана выборка - множество пар значений свободной и зависимой переменной,
.
Свободная переменная
, зависимая переменная
.
Принята модель регрессионной зависимости - параметрическое семейство функций
в которой аддитивная случайная величина имеет Гауссово распределение с нулевым математическим ожиданием и дисперсией
.
Модель принадлежит множеству моделей
, которое задается следующим образом.
Экспертно задано конечное множество функций
.
Обозначим
некоторое подмножество множества индексов функций из
.
Пусть
- порядковый номер подмножества
,
.
Модель
есть линейная комбинация функций
с индексом
,
Индекс есть мощность множества
индексов функций из
, другими словами, число элементов в линейной комбинации
.
Найти
Требуется решить задачу восстановления линейной регрессии методом наименьших квадратов и выбрать такую модель ,
которая бы доставляла минимум сумме квадратов регрессионных остатков
Замечание. В данной постановке не рассматриваются вопросы сложности модели и вопросы переобучения, они рассматриваются в задаче выбора моделей.
Постановка задачи в векторной форме. Представим предыдущую задачу в виде задачи восстановления регрессии многих переменных.
Обозначим множество элементов выборки как векторы и
.
Обозначим вектор
Обозначим вектор-функцию
Матрица состоит из векторов-столбцов
,
, где
Требуется выбрать такую модель ,
которая бы доставляла минимум сумме квадратов регрессионных остатков
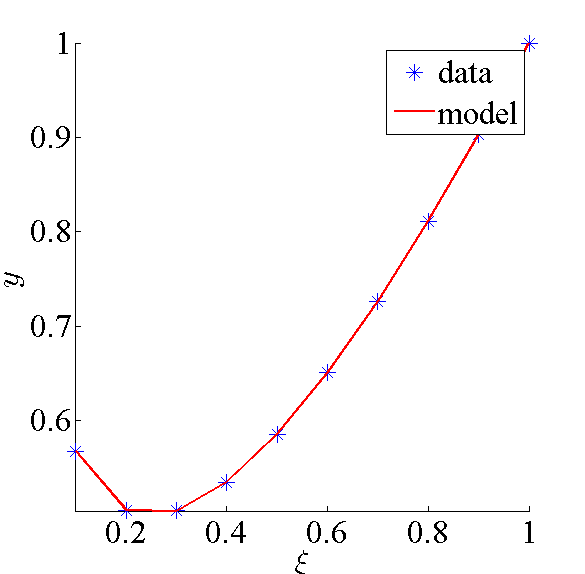
Пример
Задана выборка :
Задано множество функций :
Множество регрессионных моделей - линейных комбинаций функций из имеет вид:
Модель, доставляющая наименьшую среднеквадратичную ошибку, имеет вид