М-оценка
Материал из MachineLearning.
М-оценки — широкий класс статистических оценок, доставляющих минимум суммы каких-либо функций от данных:
М-оценками являются, в частности, оценки наименьших квадратов, а также многие оценки максимального правдоподобия.
Функция выбирается таким образом, чтобы обеспечить желаемые свойства оценки (несмещённость и эффективность) в условиях, когда данные взяты из известного распределения, и достаточную устойчивость к отклонениям от этого распределения.
M-оценки положения распределения
Для положения распределения М-оценки задаются следующим образом:
где функция должна удовлетворять требованиям
при
Среднее и медиана распределения минимизируют, соответственно, функции и
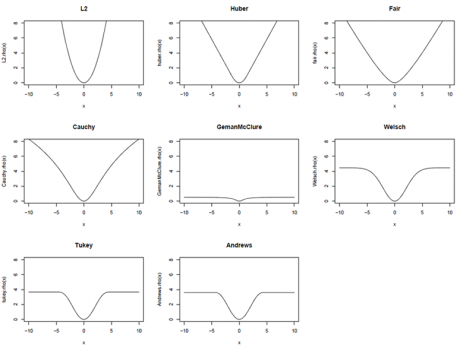
; примеры других функций
, рассматриваемых в теории робастного оценивания, приведены в таблице ниже.
Если имеет производную
, задача минимизации приводит к уравнению
Чтобы сделать М-оценку независимой от коэффициента масштаба распределения, можно перейти к задаче
где значение параметра можно находить вместе с
, а можно считать в данной задаче известным, используя какую-либо оценку (например, абсолютное отклонение среднего).
Иногда от этой задаче переходят к задаче вида
где ,
— весовая функция. Оценка параметра тогда получается как решение итерационно перевзвешиваемой задачи наименьших квадратов:
где k — номер итерации.
| М-оценка | | | |
|---|---|---|---|
| Huber | | | |
| "fair" | | | |
| Cauchy | | | |
| Geman-McClure | | | |
| Welsch | | | |
| Tukey | | | |
| Andrews | | | |
Следующая таблица содержит значения параметров методов, подобранные таким образом, чтобы при применении к стандартному нормальному распределению оценки имели асимптотическую эффективность 95%.
| М-оценка | Значение параметра |
|---|---|
| Huber | 1.345 |
| "fair" | 1.3998 |
| Cauchy | 2.3849 |
| Welsch | 2.9846 |
| Tukey | 4.6851 |
| Andrews | 1.339 |
Ссылки
- M-estimator - статья из английской Википедии