Вычисление определителя
Материал из MachineLearning.
| | Название статьи необходимо изменить. Текст статьи нуждается в существенной переработке (см. Обсуждение).--Strijov 12:53, 20 октября 2008 (MSD) |
Содержание |
Постановка задачи
Задание подразумевает знакомство пользователя с основными понятиями численных методов, такими как определитель и обратная матрица, и различными способами их вычислений. В данном теоретическом отчете простым и доступным языком сначала вводятся основные понятия и определения, на основании которых проводится дальнейшее исследование. Данная работа подразумевает, что пользователь может не иметь специальных знаний в области численных методов и линейной алгебры, но с легкостью сможет воспользоваться результатами работы. Для наглядности приведена программа вычисления определителя матрицы несколькими методами, написанная на языке программирования C++. Программа используется как лабораторный стенд для создания иллюстраций к отчету. А также проводится исследование методов для решения систем линейных алгебраических уравнений. Доказывается бесполезность вычисления обратной матрицы, поэтому в работе приводится более оптимальные способы решения уравнений не вычисляя ее. Рассказывается почему существует такое количество различных методов вычисления определителей и обратных матриц и разбираются их недостатки. Также рассматриваются погрешности при вычислении определителя и оценивается достигнутая точность. Помимо русских терминов в работе используются и их английские эквиваленты для понимания, под какими названиями искать численные процедуры в библиотеках и что означают их параметры.
Алгоритм решения
Основная идея решения: для наиболее полного раскрытия темы исследования вычисления обратной матрицы и определителя написан теоретический отчет, в котором простым и доступным языком сначала вводятся основные понятия и определения, на основании которых проводится дальнейшее исследование. Данная работа подразумевает, что пользователь может не иметь специальных знаний в области численных методов и линейной алгебры, но с легкостью сможет воспользоваться результатами работы. Для наглядности приведена программа вычисления определителя матрицы несколькими методами, написанная на языке программирования C++. А также проводится исследование методов для решения систем линейных алгебраических уравнений. Доказывается бесполезность вычисления обратной матрицы, поэтому в работе приводится более оптимальные способы решения уравнений не вычисляя ее.
Определитель
Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка , нужно уже знать, что такое определитель матрицы порядка
. Отметим также, что определитель существует только у квадратных матриц.
Определитель квадратной матрицы будем обозначать
или det
.
Определение 1. Определителем квадратной матрицы 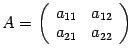 второго порядка называется число
второго порядка называется число ![]() .
.
Определителем 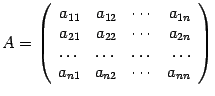 квадратной матрицы порядка
квадратной матрицы порядка ,
, называется число
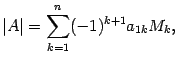
где - определитель матрицы порядка
, полученной из матрицы
вычеркиванием первой строки и столбца с номером
.
Для наглядности запишем, как можно вычислить определитель матрицы четвертого порядка: 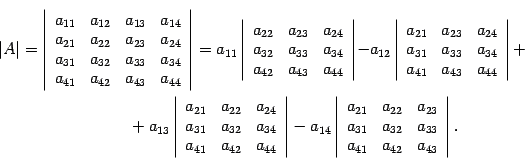
Замечание. Реальное вычисление определителей для матриц выше третьего порядка на основе определения используется в исключительных случаях. Как правило, вычисление ведется по другим алгоритмам, которые будут рассмотрены позже и которые требуют меньше вычислительной работы.
Замечание. В определении 1 было бы точнее сказать, что определитель есть функция, определенная на множестве квадратных матриц порядка и принимающая значения в множестве чисел.
Замечание. В литературе вместо термина "определитель" используется также термин "детерминант", имеющий тот же самый смысл. От слова "детерминант" и появилось обозначение det .
Рассмотрим некоторые свойства определителей, которые сформулируем в виде утверждений.
Обратная матрица
Вычисление определителя и обратной матрицы с помощью метода Гаусса
Прагматика
Классификация методов
Обращение матрицы методом Гаусса
Вычисление определителя методом триангуляции
Примеры работы алгоритма
Руководство пользователя
Руководство программиста
Литература
- http://e-lib.gasu.ru/eposobia/metody/
- http://www.exponenta.ru/educat/systemat/slivina/lection/lection2/lection2.asp
- http://elib.ispu.ru/library/math/sem1/index.html
- Киселёв В.Ю., Пяртли А.С., Калугина Т.Ф. Высшая математика.
- Боглаев Ю.П. Вычислительная математика и программирование. - М., Высшая школа, 1990, 544с.

