Методы оптимизации в машинном обучении (курс лекций)/2012/Задание 2

Материал из MachineLearning.

Версия от 11:59, 3 ноября 2012; Kropotov (Обсуждение | вклад)
(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)
Перейти к: навигация, поиск
Основная статья: Методы оптимизации в машинном обучении (курс лекций)

Начало выполнения задания: 27 октября 2012

Срок сдачи: 16 ноября (пятница), 23:59

Среда реализации задания – MATLAB.

Логистическая регрессия

Иллюстрация работы логистической регрессии
Иллюстрация работы логистической регрессии
Построение нелинейного решающего правила с помощью логистической регрессии с радиальными базисными функциями
Построение нелинейного решающего правила с помощью логистической регрессии с радиальными базисными функциями
Иллюстрация разреженного решающего правила, полученного с помощью -регуляризованной логистической регрессии с радиальными базисными функциями. Релевантные объекты обозначены черными кругами.
Иллюстрация разреженного решающего правила, полученного с помощью L_1-регуляризованной логистической регрессии с радиальными базисными функциями. Релевантные объекты обозначены черными кругами.

Формулировка метода

Рассматривается задача классификации на два класса. Имеется обучающая выборка \{\vec{x}_n,t_n\}_{n=1}^N, где \vec{x}_n\in\mathbb{R}^D — вектор признаков для объекта n, а t_n\in\{-1,+1\} — его метка класса. Задача заключается в предсказании метки класса t_{new} для объекта, представленного своим вектором признаков \vec{x}_{new}.

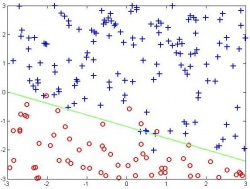
В логистической регрессии предсказание метки класса осуществляется по знаку линейной функции:

t(\vec{x}_{new}) = \mathrm{sign}(\vec{w}^T\vec{x}_{new}),

где \vec{w}\in\mathbb{R}^D — некоторые веса. Для учета линейного сдвига в данном решающем правиле в вектора признаков добавляется единица: [\vec{x}^T,\ 1]^T. Настройка весов осуществляется путем минимизации следующего регуляризованного критерия:

J = \frac{1}{N}\sum_{n=1}^N\log(1+\exp(-t_n\vec{w}^T\vec{x}_n)) + \lambda||\vec{w}||^2\rightarrow\min_{\vec{w}}.

Здесь \lambda\ge 0 — задаваемый пользователем параметр регуляризации. Использование регуляризации позволяет снизить вероятность переобучения алгоритма.

Использование радиальных базисных функций

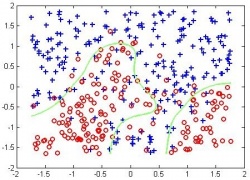
Одним их стандартных способов обобщения логистической регрессии на случай построения нелинейных разделяющих поверхностей является использование т.н. радиальных базисных функций. Здесь решающее правило заменяется на следующее:

t(\vec{x}_{new}) = \mathrm{sign}(\sum_{j=1}^Mw_j\phi_j(\vec{x}_{new})) = \mathrm{sign}(\vec{w}^T\vec{\phi}(\vec{x}_{new})),

где базисные функции \phi_j:\mathbb{R}^D\rightarrow\mathbb{R} определяются как

\phi_j(\vec{x}) = \exp(-\gamma||\vec{x}-\vec{x}_j||^2).

Здесь \gamma>0 — параметр, а \vec{x}_j — j-ый объект обучающей выборки.

Использование 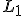L_1-регуляризации

В логистической регрессии использование L_1-регуляризации вместо квадратичной соответствует решению следующей задачи оптимизации на этапе обучения:

\frac{1}{N}\sum_{n=1}^N\log(1+\exp(-t_n\vec{w}^T\vec{\phi}(\vec{x}_n))) + \lambda\sum_{j=1}^D|w_j|\rightarrow\min_{\vec{w}}.

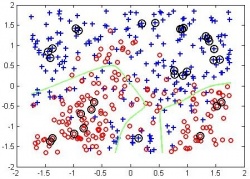
Известно, что решение такой задачи обладает свойством разреженности, т.е. часть компонент оптимального вектора весов \vec{w} равно нулю. С точки зрения линейного решающего правила \mathrm{sign}(\vec{w}^T\vec{\phi}(\vec{x})) нулевые веса равносильны исключению соответствующей базисной функции (или исходного признака) из модели.

Формулировка задания

  • Реализовать процедуру обучения логистической регрессии с квадратичной регуляризацией с помощью трех подходов:
    1. Метод Ньютона с ограниченным шагом (damped Newton) и адаптивным подбором длины шага,
    2. Метод L-BFGS с подбором длины шага через backtracking,
    3. Метод на основе верхней оценки Йаакколы-Джордана для логистической функции, в котором на этапе решения СЛАУ используется метод сопряженных градиентов;
  • Провести тестирование разработанных методов на модельных данных. Необходимо исследовать различные сочетания количества объектов и признаков (кол-во признаков значительно меньше кол-ва объектов, величины сравнимы между собой, кол-во признаков больше кол-ва объектов). Также необходимо особое внимание уделить случаю данных большого объема. Кроме того, необходимо исследовать поведение методов для различных показателей точности \varepsilon;
  • Реализовать процедуру обучения L_1-регуляризованной логистической регрессии с помощью метода на основе верхней оценки Йааккола-Джордана для логистической функции и квадратичной оценки для функции модуля, в котором на этапе решения СЛАУ используется метод сопряженных градиентов;
  • Провести тестирование разработанного метода на модельных данных для различных сочетаний количества объектов и признаков, особое внимание при этом необходимо уделить ситуации, когда число признаков превосходит число объектов, и случаю данных большого объема. Среди модельных данных рассмотреть различные сочетания между количеством релевантных и шумных признаков. Необходимо также исследовать поведение метода при изменении точности \varepsilon;
  • Написать отчет в формате PDF с описанием всех проведенных исследований. Данный отчет должен содержать, в частности, необходимые формулы для методов с использованием верхних оценок: вид оптимизируемого функционала и формулы пересчета параметров. Также во всех приведенных экспериментах должно быть указано количество итераций, точность, параметры и время работы методов.

Спецификация реализуемых функций

Минимизация функции с помощью метода Ньютона с ограниченным шагом
[x, f] = min_dampednewton(func, x0, param_name1, param_value1, ...)
ВХОД
func — указатель на минимизируемую функцию;
x0 — начальное приближение, вектор;
(param_name, param_value) — необязательные параметры, следующие названия и значения возможны:
'eps' — точность оптимизации по функции и аргументу, число, по умолчанию = 1e-5;
'params' — параметры процедуры адаптивной коррекции длины шага, вектор из двух чисел [alpha, v], где alpha — начальное значение длины шага, а v — мультипликатор шага;
'max_iter' — максимальное число итераций, число, по умолчанию = 100;
'display' — режим отображения, true или false, если true, то отображаются номер итерации, текущее значение функции, норма разности между аргументами на последней и предпоследней итерациях и др. показатели, по умолчанию = false;
ВЫХОД
x — найденное значение аргумента, вектор длины D;
f — значение функции в точке оптимума x, число.

Прототип функции min_lbfgs для минимизации функции с помощью метода L-BFGS выглядит аналогично, 'params' определяет параметры метода backtracking для поиска оптимальной длины шага на очередной итерации. Возможным значением 'params' является вектор из трех чисел [alpha beta rho], где alpha — начальная длина шага, beta — делитель шага, rho — параметр из первого условия Флетчера.

Вычисление функционала для L_2-регуляризованной логистической регрессии
[f, g, H] = l2logreg(w, X, t, lambda)
ВХОД
w — вектор весов;
X — обучающая выборка, матрица размера N x D, где N — число объектов, а D — число признаков;
t — метки классов для обучающей выборки, вектор длины N со значениями +1 и -1;
lambda — значение параметра регуляризации, число;
ВЫХОД
f — значение функционала J, число;
g — значение градиента J, вектор длины D, вычисляется только при необходимости;
H — значение гессиана J, матрица размера D x D, вычисляется только при необходимости.

 

Обучение логистической регрессии с помощью верхних оценок
[w, f] = logreg_ub(X, t, lambda, w0, param_name1, param_value1, ...)
ВХОД
X — обучающая выборка, матрица размера N x D, где N — число объектов, D — число признаков;
t — метки классов для обучающей выборки, вектор длины N со значениями +1 и -1;
lambda — значение параметра регуляризации, число;
w0 — начальный вектор весов, вектор длины D;
(param_name, param_value) — необязательные параметры, следующие названия и значения возможны:
'regul' — вид регуляризации, строка, возможные значения 'L2' и 'L1', по умолчанию = 'L2';
'LS' — стратегия для решения промежуточных СЛАУ, строка, по умолчанию = 'chol', возможные значения:
'chol' — разложение Холецкого, эквивалентно матлабовской операции A\b;
'cg-full' — метод сопряженных градиентов, в котором операция умножения матрицы A на вектор w выполняется непосредственно;
'cg-cons' — метод сопряженных градиентов, в котором операция вида (X^TX + \lambda I)\vec{w} реализуется как \vec{w}_1 = X\vec{w},\ \vec{w}_2 = X^T\vec{w}_1,\ \vec{w}_3 = \vec{w}_2+\lambda\vec{w}.
'eps' — точность оптимизации по функции и аргументу, число, по умолчанию = 1e-5;
'max_iter' — максимальное число итераций, число, по умолчанию = 100;
'display' — режим отображения, true или false, если true, то отображаются номер итерации, текущее значение верхней границы, норма разности между весами на последней и предпоследней итерациях и др. показатели, по умолчанию = false;
ВЫХОД
w — найденное значение весов, вектор длины D;
f — значение верхней границы (совпадает с самой функцией) в точке оптимума w, число.

Обратите внимание, что точность решения СЛАУ при использовании метода сопряженных градиентов должна превышать заданную точность eps.

Оформление задания

Выполненный вариант задания необходимо прислать письмом по адресу bayesml@gmail.com с темой «[МОМО12] Задание 2. ФИО». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Также убедительная просьба строго придерживаться заданной выше спецификации реализуемых функций.

Письмо должно содержать:

  • PDF-файл с описанием проведенных исследований;
  • Файлы min_dampednewton.m, min_lbfgs.m, l2logreg.m, logreg_ub;
  • Набор вспомогательных файлов при необходимости.
Источник — «http://recognition.su/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4%D1%8B_%D0%BE%D0%BF%D1%82%D0%B8%D0%BC%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D0%B8_%D0%B2_%D0%BC%D0%B0%D1%88%D0%B8%D0%BD%D0%BD%D0%BE%D0%BC_%D0%BE%D0%B1%D1%83%D1%87%D0%B5%D0%BD%D0%B8%D0%B8_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%29/2012/%D0%97%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5_2»