Математические основы теории прогнозирования (курс лекций)
Материал из MachineLearning.
|
Курс посвящен математическим методам обработки информации, основанных на выделении структуры в исходных данных и ее последующем анализе. Эти методы широко используются при решении задач из разных прикладных областей, включая обработку изображений и видео, анализ поведения, распознавание речи, машинное обучение.
Программа курса
ЧАСТЬ 1 (лектор Д.П. Ветров)
Различные постановки задач машинного обучения
Обзор задач анализа данных: классификация, регрессия, кластеризация, идентификация, прогнозирование. Примеры. Историческая справка. Основные проблемы теории распознавания образов: переобучение, противоречивость информации, малый объем выборки. Иллюстративные примеры переобучения, связь переобучения и объема выборки.
Ликбез: основные понятия теории вероятностей (математическое ожидание, дисперсия, ковариационная матрица, плотность вероятности, функция правдоподобия)
Методы линейной и логистической регрессии. Регуляризация обучения.
Метод максимального правдоподобия. Формальные обозначения, генеральная совокупность, критерии качества обучения как точности на генеральной совокупности. Вывод выражения для идеальных решающих правил. Способы введения функции правдоподобия для задачи регрессии и классификации. Выражение для коэффициентов линейной регрессии, хэт-матрица. Метод наименьших квадратов с итеративно-перевзвешивающимися весами. Необходимость ридж-оценивания для устранения вырожденности гессиана.
Ликбез: нормальное распределение, псевдообращение матриц и нормальное псевдорешение.
Метод опорных векторов
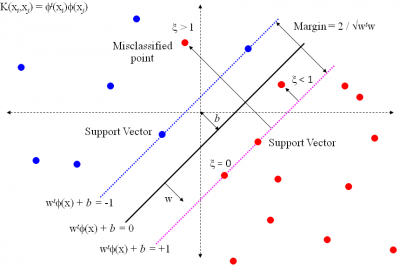
Линейный классификатор, максимизирующий зазор между классами. Обучение классификатора как задача квадратичного программирования. Получение двойственной задачи для задачи квадратичного программирования. Ядровой переход. Опорные объекты. Настройка параметров метода.
Ликбез: решение задач условной оптимизации, правило множителей Лагранжа, переход к двойственной задаче
Скрытые марковские модели (СММ). Алгоритм сегментации сигнала.
Примеры задач сегментации сигналов. Обучение СММ с учителем. Поиск наиболее вероятной последовательности состояний. ЕМ-алгоритм и его использование для решения задачи кластеризации.
Ликбез: динамическое программирование
Обучение СММ без учителя
Алгоритм Баума-Уэлша для подсчета условного распределения скрытой переменной в отдельной точке. ЕМ-алгоритм для обучения СММ без учителя. Особенности численной реализации на ЭВМ. Модификации СММ (СММ высших порядков, факториальные СММ, многопоточные СММ, СММ ввода-вывода). Примеры использования СММ.
ЧАСТЬ 2 (лектор Ю.И. Журавлев)
Литература
- Дьяконов А.Г. Алгебра над алгоритмами вычисления оценок: Учебное пособие.– М.: Издательский отдел ф-та ВМиК МГУ им. М.В. Ломоносова, 2006. – 72с. (ISBN 5-89407-252-2)
- Журавлёв Ю.И. Избранные научные труды. – М.: «Магистр», 1998.– 420с.
- Ветров Д.П., Кропотов Д.А. Байесовские методы машинного обучения, учебное пособие по спецкурсу, 2007 (Часть 1, PDF 1.22МБ; Часть 2, PDF 1.58МБ)
- Bishop C.M. Pattern Recognition and Machine Learning. Springer, 2006.
Ссылки
Машинное обучение (курс лекций, К.В. Воронцов)
Алгоритмы, модели, алгебры (курс лекций, Ю.И. Журавлев, А.Г. Дьяконов)
Байесовские методы машинного обучения (спецкурс, Д.П. Ветров, Д.А. Кропотов, А.А. Осокин)
Структурные методы анализа изображений и сигналов (спецкурс, Д.П. Ветров, Д.А. Кропотов, А.А. Осокин)