Описание окрестности точки наибольшего правдоподобия моделей (пример)

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

Постановка задачи

Пусть задана выборка D = \{(\mathbf{x}^i, y^i\)} из m пар.

\{\mathbf{x}^i\}^m_{i=1} - множество из m объектов, \mathbf{x}^i = [x^i_1, \ldots, x^i_n]^T \in\mathbb{R}^n , где n - количество признаков, а y^i\in\mathbb{R} - соответствующая зависимая переменная.

\mathbf{x}_j = [x^1_j, \ldots, x^m_j]^T \in\mathbb{R}^m - вектор значений j-ого признака, а \mathbf{y} = [y^1, \ldots, y^m]^T \in\mathbb{R}^m - вектор целевого признака.


D = ([\mathbf{x}_1, \ldots, \mathbf{x}_n], \mathbf{y}) = (X, \mathbf{y})


Пусть I = \{1, \ldots, m\} - множество индексов объектов, J = \{1, \ldots,n\} - множество индексов признаков. A\subseteq J - подмножество активных признаков. Множество A задаёт регрессионную модель f_A, а c_f = |A| - сложность модели.

Рассмотрим следующую линейную модель регрессии, описывающую связь между свободными и зависимой переменными


\mathbf{y} = f_A(X, \mathbf{w}) + \mathbf{\varepsilon} = X \mathbf{w} + \mathbf{\varepsilon} ,       (1)


где \mathbf{w} = [\ldots, w_j, \ldots]^T_{j\in A} - вектор параметров регрессии, а случайная аддитивная переменная \mathbf{\varepsilon} регрессионной модели имеет нормальное распределение \varepsilon \in N(0, \sigma^2).


Распределение зависимой переменной будет иметь следующий вид:

p(y|x, \mathbf{w}, \sigma^2, f) = \frac{exp(-\frac{1}{\sigma^2}S)}{(2\pi\sigma^2){\frac{n}{2}}},


где S - сумма квадратов невязок y^i - f(\mathbf{x}^i, \mathbf{w}). Согласно оценки точки наибольшего правдоподобия, данное распределение задаёт критерий качества модели, равный сумме квадратов регрессионных остатков.

S = \sum_{i\in \Theta} (y^i - f(\mathbf{x}^i, \mathbf{w}))^2 ,       (2)


где \Theta \subseteq I - некоторое множество индексов. Этот критерий используется при выборе модели в дальнейшем.


Мультиколлинеарность отслеживается с помощью фактора инфляции дисперсии (VIF), связанного с корреляцей данного признака с другими:


VIF_j = \frac{1}{1 - R_j^2}        (3)


Коэффициент детерминации j-ого признака относительно остальных вычисляется следующим образом:

R_j^2 = 1 - \frac{||\mathbf{x}_j - X_{A\setminus\{j\}\mathbf{w}}||^2}{||\mathbf{x}_j - 1 \overline{x_j}||^2},

где \overline{x_j} - среднее значение вектроа \mathbf{x}_j


Требуется найти такую модель оптимальной структуры признаков F, которая доставляет наименьшее значение функционалу качества (2).

Порождение свободных переменных

Множества измеряемых признаков бывает недостаточно для построения модели удовлетворительного качества. Требуется расширить множество признаков с помощью функциональных преобразований.

Предлагается следующий способ порождения новых признаков:

Пусть задано множество свободных переменных Z = \{\xi_u\}^U_{u=1} и конечное множество порождающих функций G = \{g_v\}^V_{v=1}.

Обозначим a_i = g_v(\xi_u), где индекс i = (v - 1)U + u.

Рассмотрим декартово произведение Z \times G, где элементу (g_v,\xi_u) ставится в соответствие суперпозиция g_v(\xi_u), однозначно определяемая индексами v,u.

В качестве модели, описывающей отношение между зависимой переменной y и свободными переменными a_i, используется полином Колмогорова-Габора:


y=w_0+\sum_{\alpha=1}^{UV}w_{\alpha}a_{\alpha} + \sum_{\alpha=1}^{UV}\sum_{\beta=1}^{UV}w_{{\alpha}{\beta}}a_{\alpha}a_{\beta} + \ldots +\sum_{\alpha=1}^{UV}\ldots\sum_{\psi=1}^{UV}w_{{\alpha} \ldots {\psi}}a_{\alpha}\ldots a_{\psi}
,


где \mathbf{w} = (w_0, w_{\alpha}, w_{\alpha\beta}, \ldots , w_{{\alpha} \ldots {\psi}})^T и {\alpha, \beta, \ldots , \psi = 1 \ldots UV}.


\{0\} \cup \{\alpha\} \cup \{\alpha,\beta\} \cup \ldots \cup \{\alpha,\beta \ldots \psi\} \rightarrow \Omega - множество индексов, размерности N.

\xi_u~ \longrightarrow\longrightarrow\longrightarrow^{g_v}\longrightarrow\longrightarrow ~g_v(\xi_u) ~=^{def} a_i~\longrightarrow\longrightarrow^{\prod^{UV}_{\alpha=1}}\longrightarrow^{\ldots}\longrightarrow^{\prod^{UV}_{\psi=1}}\longrightarrow ~x_j

Алгоритм

Рассмотрим алгоритм, состоящий из двух шагов.

На первом шаге мы будем добавлять признаки один за другим к нашей модели согласно критерию качества модели (2).

На втором шаге мы будем удалять признаки по одному из нашей модели согласно тому же критерию качества (2).

Пусть на k-ом шагу алгоритма имеется множество признаков A, которое определяет матрицу X_A: \mathbf{y} = X_A \mathbf{w}.

На нулевом шаге A_0 = \emptyset. Опишем k-ый шаг алгоритма.


Шаг 1: добавление признаков

Добавляем такой признак j \in J \setminus A_{k-1} к активному набору A_k = A_{k-1} \cup \{j\}, который доставляет минимум функционалу (2).


j = \arg\min_{j\in J \setminus A_{k-1}} S(X_A_k, \mathbf{y})


Пусть
k^* = \arg\max_{t=1,\ldots,k} Evidence_t

Если выполнено условие:

k - k^* \geq d,

то идём к шагу 2, иначе - повторяем шаг 1.

d - заданная константа.


Шаг 2: удаление признаков

Удаляем такой признак j \in A_{k-1} из активного набора A_k = A_{k-1} \setminus \{j\}, который имеет наибольший фактора инфляции дисперсии, то есть доставляет максимум функционалу (3).


j = \arg\max_{j\in A_{k-1}} VIF_j


Пусть
k^* = \arg\max_{t=1,\ldots,k} Evidence_t

Если выполнено условие:

k - k^* \geq d,

то идём к шагу 1, иначе - повторяем шаг 2.

d - заданная константа.

Критерий останова

Алгоритм заканчивает работу, если правдоподобие Evidence_k перестаёт увеличиваться.

Тогда мы нашли оптимальный набор признаков.

Вычислительный эксперимент

Порождение новых признаков: 

G = [Z, Z.^2, tan(Z), exp(Z)]; %множество порождающих функиций m на V*U
X = [ones(m,1), G]; %множество признаков m на N
 
N = size(X,1)
for i = 1 : U*V
    for j = 1 : U*V
        if i >= j
            X = [X, G(:,i).*G(:,j)];
            N = N + 1;
        end
    end
end

Вычисление функционала качества (2): 

[w, sse_] = lsqlin(X_mask,target,[],[]);
 
if sse_ < sse_best% & sse_ < sse_last
    sse_best = sse_;
    index_best = ind(i);
    changed = 1;
end

Вычисление правдоподобия: 

xRegression=X_;
yRegression=target;
 
[n,m] = size(xRegression);
activeSet = 1:m; % количество активных признаков
 
[weightM,alphaM,beta,weightH,alphaMH,betaH,gammaH] = ...
     getLinParam(xRegression,yRegression,activeSet);
evid_ = -abs (getEvid( xRegression,yRegression,weightM,alphaM,beta ))


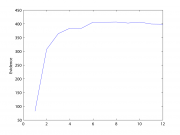
На графике выведем зависимость правдоподобия(ocь Y) от шага алгоритма(ось X) 

evidence
plot(linspace(1,numel(evidence),numel(evidence)), evidence);



Эксперимент 1.

Количество объектов = 300, количество начальных признаков = 6, количество признаков = 230

Порождающие функции: g = \{x,~x^2,~\tan(x),~\exp(x)\}





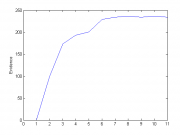
Эксперимент 2.

Количество объектов = 300, количество начальных признаков = 6, количество признаков = 230

Порождающие функции: g = \{x,~x^2,~\tan(x),~\exp(x)\}





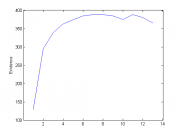
Эксперимент 3.

Количество объектов = 500, количество начальных признаков = 6, количество признаков = 230

Порождающие функции: g = \{x,~x^2,~\tan(x),~\exp(x)\}

Литература

  1. Стрижов В.В Методы выбора регрессионных моделей. — ВЦ РАН, 2010.
  2. Стрижов В.В Методы индуктивного порождения регрессионных моделей. — ВЦ РАН, 2008.
  3. Vadim Strijov, Katya Krymova, Gerhard Wilhelm Weber Evidence Optimization for Consequently Generated Models. — Computing Center of the Russian Academy of Science, Moscow, Russia, 2010.
Источник — «http://recognition.su/wiki/index.php?title=%D0%9E%D0%BF%D0%B8%D1%81%D0%B0%D0%BD%D0%B8%D0%B5_%D0%BE%D0%BA%D1%80%D0%B5%D1%81%D1%82%D0%BD%D0%BE%D1%81%D1%82%D0%B8_%D1%82%D0%BE%D1%87%D0%BA%D0%B8_%D0%BD%D0%B0%D0%B8%D0%B1%D0%BE%D0%BB%D1%8C%D1%88%D0%B5%D0%B3%D0%BE_%D0%BF%D1%80%D0%B0%D0%B2%D0%B4%D0%BE%D0%BF%D0%BE%D0%B4%D0%BE%D0%B1%D0%B8%D1%8F_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B5%D0%B9_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»