Персептрон
Материал из MachineLearning.
Перце́птрон (Персептрон[1], англ . perсeptron от лат. perсeptio — восприятие) — устройство МАРК-1 [1], а так же соответствующая ему компьютерная модель, созданная Фрэнком Розенблаттом с целью построения модели мозга. Под «моделью мозга» понимается любая теоретическая система, которая стремится объяснить физиологические функции мозга с помощью известных законов физики и математики, а также известных фактов нейроанатомии и нейрофизиологии. Перцептрон (строгое определение которого будет дано ниже) представляет собой передающую сеть, состоящую из генераторов сигнала трёх типов: сенсорных элементов, ассоциативных элементов и реагирующих элементов. Производящие функции этих элементов зависят от сигналов, возникающих либо где-то внутри передающей сети, либо, для внешних элементов, от сигналов, поступающих из внешней среды. Но, как правило, когда говорится "перцептрон Розенблатта", имеется в виду частный случай — т. н. элементарный перцептрон, который упрощён по сравнению с общим видом перцептрона по ряду параметров.
Появление перцептрона
В середине 1958 года Фрэнк Розенблат предложил модель электронного устройства, названного им перцептроном, которое должно было бы имитировать процессы человеческого мышления. Перцептрон должен был передавать сигналы от «глаза», составленного из фотоэлементов, в блоки электромеханических ячеек памяти, которые оценивали относительную величину электрических сигналов. Эти ячейки соединялись между собой случайным образом в соответствии с принципами коннективизма. Два года спустя была продемонстрирована первая действующая машина «Марк-1», которая могла научится распознавать некоторые из букв, написанных на карточках, которые подносили к его «глазам», напоминающие кинокамеры.
Чтобы "научить" перцептрон способности строить догадки на основе исходных предпосылок, в нем предусматривалась некая элементарная разновидность автономной работы или «самопрограммирования». При распознании той или иной буквы одни ее элементы или группы элементов оказываются гораздо более существенными, чем другие. Перцептрон мог "научаться" выделять такие характерные особенности буквы полуавтоматически, своего рода методом проб и ошибок, напоминающим процесс обучения. Однако возможности перцептрона были ограниченными: машина не могла надежно распознавать частично закрытые буквы, а также буквы иного размера или рисунка, нежели те, которые использовались на этапе ее обучения.
Ведущие представители так называемого «нисходящего метода» специализировались, в отличие от представителей «восходящего метода», в составлении для цифровых компьютеров общего назначения программ решения задач, требующих от людей значительного интеллекта, например для игры в шахматы или поиска математических доказательств. К числу защитников «нисходящего метода» относились сотрудники Массачусетского технологического института Марвин Минский и Сеймур Пейперт, . Минский начал свою карьеру исследователя ИИ сторонником «восходящего метода» и в 1951 году построил обучающуюся сеть на вакуумных электронных лампах. Однако вскоре к моменту создания перцептрона он перешел в противоположный лагерь.
В соавторстве с южно-африканским математиком Пейпертом он опубликовал в 1969 г. книгу «Перцептроны», где математически доказывалось, что перцептроны, подобные розенблатовским, принципиально не в состоянии выполнять многие из тех функций, которые приписывал перцептронам Розенблат. Минский утверждал, что, не говоря уже о роли работающих под диктовку машинисток, подвижных роботов или машин, способных читать, слушать и понимать прочитанное или услышанное, перцептроны никогда не обретут даже умения распознавать предмет частично заслоненный другим. Глядя на торчащий из-за кресла кошачий хвост, подобная машина никогда не сможет понять, что она видит. Эта книга существенно повлияла на пути развития науки об искусственном интеллекте, т.к. переместила научный интерес и субсидии правительственных организаций США, традиционно финансирующих исследования по ИИ, на другое направление исследований — «нисходящий метод».
В 80-х гг. интерес к кибернетике возродился, так как сторонники «нисходящего метода» столкнулись со столь же неодолимыми трудностями. Сам Минский публично выразил сожаление, что его выступление нанесло урон концепции перцептронов, заявив, что, согласно его нынешним представлениям, для реального прорыва вперед в создании разумных машин потребуется устройство, во многом похожее на перцептрон. Но в основном ИИ стал синонимом нисходящего подхода, который выражался в составлении все более сложных программ для компьютеров, моделирующих сложную деятельность человеческого мозга.
Определения, данные Ф. Розенблаттом
Серьезное ознакомленние с теорией перцептронов требует знания базовых определений и теорем, совокупность которых и представляет собой базовую основу для всех последующих видов искусственных нейронных сетей
Виды элементов (нейронов) в перцептроне
- Определение 7. Простым S-элементом (Сенсорным элементом) является чувствительный элемент, который от воздействия какого-либо из видов энергии (например, света, звука, давления, тепла и т. п.) вырабатывает сигнал. Если входной сигнал <math>c_{wi}^{*}</math> превышает некоторый порог <math>\theta_{i}</math>, то элемент выдаёт выходной сигнал <math>S_{i}^{*} = +1 </math> , в противном случае выходной сигнал равен нулю.
- Определение 9. Простым A-элементом (Ассоциативным элементом) называется логический решающий элемент, который выдаёт выходной сигнал, когда алгебраическая сумма его входных сигналов <math>a_i</math> равна или превышает некоторую пороговую величину <math>\theta_{i}>0</math>. Выходной сигнал <math>a_{i}^{*}</math> равен +1, если была превышена пороговая величина <math>\theta_{i}</math>; в противном случае он равен нулю. Если <math>a_{i}^{*} = +1</math>, то говорят, что A-элемент является активным.
- Определение 11. Простым R-элементом (Реагирующим элементом) называется элемент, который выдаёт выходной сигнал <math>r^{*} = +1 </math>, если сумма его входных сигналов является строго положительной, и сигнал <math>r^{*} = -1 </math>, если сумма его входных сигналов является строго отрицательной. Если сумма входных сигналов равна нулю, выход можно считать либо равным нулю, либо неопределённым.
Определения и классификация перцептронов
- Определение 17. Перцептрон представляет собой сеть, состоящую из S, A, R — элементов, с переменной матрицей взаимодействия V (элементы которой <math>v_{ij}</math> - весовые коэффициенты), определяемой последовательностью прошлых состояний активности сети.
- Определение 18. Логическое расстояние от элемента <math>u_{i}</math> к элементу <math>u_{j}</math> равно числу слоёв между ними.
- Определение 19. Перцептроном с последовательными связями называется система, в которой все связи, начинающиеся от элементов с логическим расстоянием d от ближайшего S-элемента, оканчиваются на элементах с логическим расстоянием d+1 от ближайшего S-элемента.
- Определение 20. Перцептроном с перекрестными связями называется система, в которой некоторые связи соединяют друг с другом элементы одного типа (S, A или R), находящиеся на одинаковом логическом расстоянии от S-элементов, причем все остальные связи — последовательного типа.
- Определение 21. Перцептроном с обратной связью называется система, в которой по крайней мере один элемент A или R, находящийся на расстоянии <math>d_{1}</math> от ближайшего S-элемента, является исходным в цепи обратной связи к S-элементу или A-элементу, расстояние которого до ближайшего S-элемента <math>d_{2}<d_{1}</math>; другими словами, это система с обратными связями от элементов, расположенных ближе к выходу, к элементам, расположенным ближе к входу системы.
где <math>a_{i}(t)</math> – алгебраическая сумма всех сигналов, поступающих одновременно на вход элемента <math>u_{i}</math> .
- Определение 22. Простым перцептроном называется любая система, удовлетворяющая следующим пяти условиям:
- В системе имеется только один R-элемент, который связан со всеми A-элементами.
- Система представляет собой перцептрон с последовательными связями, идущими только от S-элементов к A-элементам и от A-элементов к R-элементам.
- Веса всех связей от S-элементов к A-элементам являются фиксированными (не изменяются во времени).
- Время передачи каждой связи равно либо нулю, либо фиксированной постоянной t.
- Все активирующие функции S,A,R – элементов имеют вид :
<math>u_{i}^{*}(t) = f (a_{i}(t))</math>,
- Определение 23. Элементарным перцептроном называется простой перцептрон с простыми R и A элементами, активизирующая функция которого имеет вид:
<math>c_{ij}(t) = u_{i} (t - t_{0})*v_{ij}(t))</math>.
Определения, данные М. Минским
Минский изучал свойства параллельных вычислений, частным случаем которых на то время был перцептрон. Для анализа его свойств ему пришлось переизложить теорию перцептронов на язык предикатов . Хотя такой математический аппарат позволил применить анализ только к элементарному перцептрону Розенблатта, зато он вскрыл много принципиальных ограничений для параллельных вычислений, от которых не свободен не один вид современных искусственных нейронных сетей .
Определения и классификация перцептронов на языке предикатов
Определение. Перцептроном называется устройство, способное вычислять все предикаты, линейные относительно некоторого заданного множества Ф частных предикатов.
С этой позиции перцептроны можно классифицировать следующим образом:
- 1. Перцептроны, ограниченные по диаметру. Для каждого предиката F из Ф диаметр множества точек плоскости, от которых зависит F, не превосходит некоторой фиксированной величины.
- 2. Перцептроны ограниченного порядка. Мы будем говорить, что перцептрон имеет порядок <n, если каждый элемент из Ф зависит не более, чем от n точек.
- 3. Перцептроны Гамбы. Каждый элемент из Ф может зависеть от всех точек, но должен быть линейной пороговой функцией, т.е. сам должен вычисляться перцептроном первого порядка, определенным в предыдущем пункте.
- 4. Случайные перцептроны. Именно эта модель наиболее подробно изучалась группой Розенблатта. Предикаты F представляют собой случайно выбранные булевы функции. Иначе говоря, случайные перцептроны являются перцептронами ограниченного порядка, а множество Ф порождается случайным процессом с определенной функцией распределения.
- 5. Ограниченные перцептроны. Множество Ф предикатов F бесконечно, а множество значений принимаемых коэффициентами <math>k</math>, конечно.
Описание элементарного перцептрона
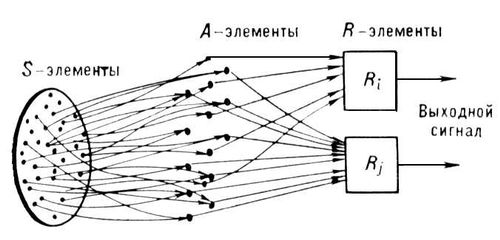
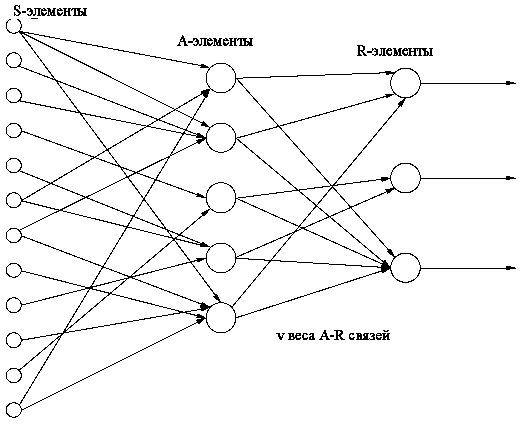
Перцепторон состоит из элементов 3-х типов: S — элементов, A — элементов и R — элемента. S — элементы это — слой рецепторов. Эти рецепторы соединены с A — элементами с помощью тормозных или возбуждающих связей. Каждый рецептор может находиться в одном из двух состояний — покоя или возбуждения. A — элементы представляют собой сумматоры с порогом (то есть формальные нейроны ). Это означает, что A — элемент возбуждается, если алгебраическая сумма возбуждений, приходящих к нему от рецепторов, превышает определенную величину — его порог. При этом сигнал от рецептора, приходящий по возбуждающей связи, считается положительным, а приходящий по тормозной связи — отрицательным. Сигналы от возбудившихся A — элементов передаются в сумматор R, причем сигнал от i-го ассоциативного элемента передается с коэффициентом ki .
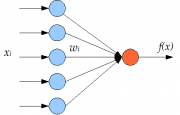
А- или R- элементы (который является пороговыми) подсчитывают некоторую линейную форму (как правило сумму весовых коэффициентов) от своих входов и сравнивает ее с заданным значением — порогом. Если у А-элемента <math>n</math> входов, то в нем должны быть заданы <math>n</math> весов <math>w_1, w_2, ..., w_n</math> и порог <math>\theta</math>. Перцептрон выдает <math>1</math>, если линейная форма от входов с коэффициентами <math>w_i</math> превышает <math>\theta</math> и <math>-1</math> иначе.
- <math>f(x) = sign(\theta + \sum_{i=1}^{n} w_i x_i)</math>
С помощью одного порогового элемента можно реализовать 14 булевых функций, кроме эквиваленции (знак равно) и исключающего или (XOR). Любая булева функция представима в виде построенной из пороговых элементов нейронной сети глубины 2.
Система связей между рецепторами S и A — элементами, так же как и пороги A — элементов выбираются некоторым случайным, но фиксированным образом, а обучение состоит лишь в изменении коэффициентов <math>w_i</math>. Считаем, что мы хотим научить перцептрон разделять два класса объектов, и потребуем, чтобы при предъявлении объектов первого класса выход перцептрона был положителен, а при предъявлении объектов второго класса — отрицательным. Начальные коэффициенты <math>w_i</math> полагаем равными нулю. Далее предъявляем обучающую выборку: объекты (например, круги либо квадраты) с указанием класса, к которым они принадлежат. Показываем перцетрону объект первого класса. При этом некоторые A — элементы возбудятся. Коэффициенты <math>w_i</math>, соответствующие этим возбужденным элементам, увеличиваем на 1. Затем предъявляем объект второго класса и коэффициенты <math>w_i</math> тех A — элементов, которые возбудятся при этом показе, уменьшаем на 1. Этот процесс продолжим для всей обучающей выборки. В результате обучения сформируются значения весов связей <math>w_i</math> .
После обучения перцептрон готов работать в режиме распознавания или обобщения В этом режиме перцептрону предъявляются «не знакомые» перцептрону объекты, и перцептрон должен установить, к какому классу они принадлежат. Работа перцептрона состоит в следующем: при предъявлении объекта возбудившиеся A — элементы передают сигнал R — элементу, равный сумме соответствующих коэффициентов <math>w_i</math>. Если эта сумма положительна, то принимается решение, что данный объект принадлежит к первому классу, а если она отрицательна — то второму.
Алгоритмы обучения
Классический метод обучения перцептрона — это обучение с коррекцией ошибки. Представляет собой такой метод обучения, при котором вес связи не изменяется до тех пор, пока текущая реакция перцептрона остается правильной. При появлении неправильной реакции вес изменяется на единицу, а знак (+/-) определяется противоположным от знака ошибки.
Кроме того, Розенблатт пытался классифицировать различные алгоритмы обучения, называя их системами подкрепления. В результате он различал следующие виды:
- Положительное подкрепление — представляет собой такой процесс подкрепления, при котором вес связи, начинающийся на активном элементе <math>u_i</math> и оканчивающийся на элементе <math>u_j</math>, изменяется на величину r, знак которой совпадает со знаком сигнала <math>u_j^*</math>.
- Отрицательное подкрепление — представляет собой такой процесс подкрепления, при котором вес связи, начинающийся на активном элементе <math>u_i</math> и оканчивающийся на элементе <math>u_j</math>, изменяется на величину r, знак которой противоположен знаку сигнала <math>u_j^*</math>.
Кроме, классического метода обучения перцептрона Розенблатт также ввел понятие об обучении без учителя, предложив следующий способ обучения:
- Альфа — системой подкрепления называется система подкрепления, при которой веса всех активных связей <math>c_{ij}</math>, которые оканчиваются на некотором элементе <math>u_j</math>, изменяются на одинаковую величину r, а веса не активных связей за это время не изменяются.
Описывая эти системы подкрепления Розенблатт основывался на идеях Хебба об обучении, уточняя различные возможные виды. Затем с появлением многослойного перцептрона оно было модифицировано и его стали называть дельта-правило . Модификация была проведена с целью сделать функцию обучения дифферинцированной, что в свою очередь нужно для применения метода градиентного спуска, благодаря которому и возможно обучение более одного слоя. При этом пришлось отказаться от бинарного сигнала, и пользоваться на входе вещественными числами.
Возможности и ограничения модели
Исследования перцептронов показали, что перцептроны способны обучаться. Справедлива теорема о сходимости перцептрона, согласно которой независимо от начальных значений коэффициентов и порядка показа образцов при обучении перцептрон за конечное число шагов научится различать два класса объектов, если только существует такая классификация.
Первые успехи исследований перцептронов и других нейросетей вызвал взрыв активности и энтузиазма. М. Минский, Ф.Розенблат, Б. Уидроу и другие разработали ряд искусственных нейронных сетей. В течение некоторого времени казалось, что ключ к интеллекту найден, и воспроизведение человеческого мозга является лишь вопросом конструирования достаточно большой сети.
Но эта иллюзия вскоре рассеялась. Возможности перцептронов оказались довольно ограниченными. Серьезный математический анализ перцептронов был проведен М.Минским и С. Пейпертом (подробнее см. ниже). В последствии работа Вассермана, вызвала новый всплеск активности в области искуственных нейронных сетей, и применение идей теории перцептронов на новый лад с образованием собственной новой терминологии и становлением науки о нейросетях, но с точки зрения технического приложения в противовес построению моделей мозга. Но к сожалению некоторые неточности в его работе привели к ряду недоразумений. Так, например, Вассерманом была предложена классификация искусственных нейроных сетей на основе подсчета числа обучаемых слоев связей, а не по числу структурных элементов сети. Но такая классификация проблематична, так как не позволяет говорить об особенностях определенного вида нейросетей. Это вызвало ряд недоразумений в последующие годы при определении перцептрона, так как сам автор всегда говорил о нем, как о трехслойном, а классификация по числу обучаемых слоев предполагала называть его однослойным. Но к сожалению, это сказалось не только на терминологии, но и не верном представлении о перцептроне как простейшем пороговом элементе. Так как была не учтена роль первого необучаемого слоя.
Структура, состоящая из нескольких соединенных слоев пороговых элементов называется многослойным перцептроном. Такой термин появился когда был предложен алгоритм обратного распространения, с помощью которого стали обучать (настраивать коэффициенты) более одного слоя. Но такую структуру не стоит прямо сравнивать с перцептроном Розенблатта. Это достаточно разные модели нейросетей, но которые во многом эквивалентны друг другу в общем случае, и специфичны для разного рода задач.
Традиционные заблуждения
В результате популяризации искуственных нейронных сетей журналистами и маркетологами был допущен ряд неточностей, которые, при недостаточном изучении оригинальных работ по этой тематике, неверно истолковывались молодыми (на то время) учеными. В результате по сей день можно встретиться с недостаточно глубокой трактовкой функциональных возможностей перцептрона по сравнению с другими ИНС, разработаными в последующие годы.
Терминологические неточности
Неточность № 1. Перцептрон — нейронная сеть без скрытых слоев.
Вассерманом была сделана попытка определенным образом классифицировать различные виды нейронных сетей:
«Как видно из публикаций, нет общепринятого способа подсчета числа слоев в сети. Многослойная сеть состоит из чередующихся множеств нейронов и весов. Входной слой не выполняет суммирования. Эти нейроны служат лишь в качестве разветвлений для первого множества весов и не влияют на вычислительные возможности сети. По этой причине первый слой не принимается во внимание при подсчете слоев, и сеть считается двухслойной, так как только два слоя выполняют вычисления. Далее, веса слоя считаются связанными со следующими за ними нейронами. Следовательно, слой состоит из множества весов со следующими за ними нейронами, суммирующими взвешенные сигналы.»
В результате такого представления перцептрон попал под определение однослойная нейроная сеть. При этом когда говорят, что перцептрон не имеет скрытых слоев, имеют в виду, что у него нет скрытых слоев обучающихся нейронов (веса которых адаптируются к задаче). Поэтому всю совокупность тех выходов системы из S и A элементов, которые достигают R-элемента (единственного обучающегося) просто логически заменяют набором (модифицированных по жесткому правилу) новых входов.
Но обычное игнорирование необучаемых слоев с фиксированными связми (который имеется в элементарном перцептроне между S и А — элементами) позволяет делать неправильные выводы о возможностях ИНС, так например, Минский поступил очень корректно переформулировав А-элемент как предикат, а например Вассермен уже потерял такое представление и у него А-элемент просто вход (почти эквивалентный S-элементу). Поэтому при такой терминалогической неточности упускается из виду тот факт, что в перцептроне происходит отображение рецепторного поля S — элементов на ассоциативное поле А-элементов, в результате чего и происходит преобразование любой нелинейной разделимой задачи в линейно разделимую.
Функциональные заблуждения
Большенство функциональных заблуждений сводятся к якобы невозможности решения перцептроном нелинейно разделяемой задачи. Но вариаций на это тему достаточно много, рассмотрим главные их них.
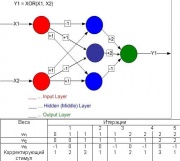
№ 1. Перцептрон не способен решить задачу XOR.
Самое несерьезное заявление. На изображении показанно решение и ниже дана таблица поиска соответствующих весов при алгоритме обучения с коррекцией ошибки. Как правило, данное заблуждение возникает из-за того, что неправильно интерпретируют определение перцептрона, данного Минским (см. выше), а именно, предикаты приравнивают входам (параметрам), хотя это разные вещи. Предикат эквивалентен входу только если предикат зависит от одного аргумента. Другая причина возникает из-за того, что перцептрон путают с пороговым элементом Маккалока-Питса.
№ 2. Выбором случайных весов можно достигнуть обучения и линейно неразделимым (вообще, любым) задачам, но только если повезет, и в новых переменных (выходах A-нейронов) задача окажется линейно разделимой. Но может и не повезти.
Теорема сходимости Розенблатта ОДНОЗНАЧНО доказывает, что не может быть ни какого «может и не повезти», при равенстве А-элементов числу стимулов и не особенной SA матрице — вероятность решения 100 %. То есть при отображении рецепторного поля на ассоциативное поле большей на одну размерность случайным (нелинейным) оператором нелинейная задача превращается в линейно разделимую. А следующий обучаемый слой уже находит линейное решение в другом пространстве входов.
№ 3. Если у Вас в задаче размерность входов довольно высока, а обучающих примеров мало, то в таком «слабозаполненном» пространстве число удач может и не оказаться малым. Это свидетельствует лишь о частном случае пригодности перцептрона, а не его универсальности.
Данный аргумент легко проверить на тестовой задаче под названием «шахматная доска» или «губка с водой»:
Дана цепочка из 2N единиц или 0. Если эта цепочка является зеркально симметричной относительно центра, то есть x[1:1:N] = x[2N:-1:N+1] то на выходе 1. Иначе 0." Обучающие примеры _все_ (это важно) 2²N цепочек. Могут быть вариации данной задачи: Имеем изображение 256х256 пикселей изображение из 2 цветов. Обучаем перцептрон всем возможным состояниям, то есть на вход подаем последовательно координаты x, y и требуем на выходе соответствующий цвет точки. В итоге имеем 65536 различных пар стимул-реакция. Берем изображение такого типа — Если либо x нечетное (0..255), либо y нечетное (но не одновременно), то цвет 1. Иначе — цвет 0. Обучить без ошибок.
Если данный аргумент справедлив, то перцептрон не сможет ни при каких условиях обучится не делая ни одной ошибки. Иначе перцептрон не ошибется ни разу.
На практике оказывается, что данная задача очень проста для перцептрона: чтобы ее решить, перцептрону достаточно 1500 А-элементов (вместо полных 65536, необходимых для любой задачи). При этом число итерациий порядка 1000. При 1000 А-элементов перцептрон не сходится за 10000 итераций. Если же увеличить число А-элементов до 40000, то схождения можно ожидать за 30-80 итераций.
№ 4. В перцептроне Розенблатта столько А-элементов, сколько входов. И сходимость по Розенблатту, это стабилизация весов.
Нет. Это следует из следствия теоремы сходимости.
Следствие 2. Если число стимулов в пространстве Ф равно n>N (то есть больше числа А-элементов элементарного перцептрона), то существует некоторая классификация С(Ф), для которой решения не существует.
Отсюда должно быть ясно, что:
- 1. у Розенблатта число А-элементов равно числу стимулов (обучающих примеров), а не числу входов.
- 2. Сходимость по Розенблатту, это не стабилизация весов, а наличие всех требуемых классификаций, то есть по сути отсутствие ошибок.
Ограничения перцептрона, описанные Минским
Действительно Минским после серьезных экспериментов с перцептроном и его всестороннего анализа была предпринята его критика. Здесь нужно отметить тот факт, что на то время все известные ИНС назывались перцептроном, и Минский критиковал именно весь класс искусственных нейронных сетей, а перцептрон Розенблатта был наиболее детально проработан теоритически и имел физическое воплощение в устройстве под названием МАРК-1. В то время была слабо развита теория о параллельных вычислениях, а перцептрон полностью соответствовал принципам таких вычислений. По большому счету Минский показал преймущество последовательных вычислений перед параллельным в определенных классах задач связанных с инвариантным представлением. Ниже мы рассмотрим некоторые следствия анализа Минского. Критику Минского можно разделить на три взаимосвязаные темы:
Ограничения, связанные с инвариантным представлением
Минский описывал специальные задачи такие как «четность» и «один в блоке», которые показывают ограничения перцептрона в том, что он не может распознавать инвариантные входные данные (изображения) бесконечного порядка. А в частности, при распознавании четности конечного порядка первый слой перцептрона вынужден становиться полносвязным. В связи с эти есть ограничения на следующие практические типовые задачи.
Типовая задача № 1. Если требуется построить машину для чтения печатных букв или цифр, то возникает естественное желание, чтобы эта машина могла распознавать их независимо от положения на странице, то есть чтобы на решение машины не оказывали влияния элементы группы переносов. Иными словами, восприятие машины должно быть «инвариантно относительно группы переносов», то есть ее решение должно быть одним и тем же для каждого представителя какого-либо класса эквивалентности относительно группы переносов. Итак, более точно первую задачу можно определить как — нахождение геометрического свойства. Вот как описывает Минский понятие геометрического свойства:
«Когда мы говорим геометрическое свойство, мы имеем в виду что-то инвариантное относительно переноса, или вращения, или растяжения. Сочетание первых инвариантностей определяет конгруэнтную группу преобразований, а наличие всех трех дает фигуры подобные в эвклидовой геометрии».
Типовая задача № 2. Ряд подзадач могут формулироваться различно, как (1) определить, одна или более фигур находятся в видимом пространстве, (2) плотная ли видимая фигура или же в ней находится отдельная фигура, (3) … . Независимо от этого они имеют общую суть — нахождение признака, связана ли фигура, то есть предиката связанность.
Типовая задача № 3. Распознавание фигур в контексте, то есть, например, содержит ли данная фигура прямоугольник и, быть может, что-то еще.
Так вот, приведенные здесь три типа задач распознавания не рекомендуется решать с помощью параллельных способов вычислений, в том числе и с помощью перцептрона. Более того, проблема не в конкретной архитектуре перцептрона, а в необходимости знания всего глобального контекста. Поэтому как перцептрон, так и любые другие виды нейронных сетей неспособны полноценно решить представленные здесь задачи. Мы не приводим здесь довольно сложные доказательства Минского, важно лишь, что они основываются на том, что перцептрон (равно как и любая другая нейронная сеть) не справляется с распознаванием инвариантных входных данных.
Ограничения, связаные с возможностью прогнозирования
Способности ИНС и в частности перцептрона, не столь велики как рекламируется. И это связано даже не с устройством, или алгоритмом, осуществляющим прогноз, а с самим происходящим явлением. Только в том случае когда во внимание берутся существенные параметры на основании которых будет строится прогноз будет иметь место некоторый успех. Выбором этих параметров занимаются эксперты в определенной области на основании своего опыта и интуиции, и к прогнозирующим машинам это не имеет ни какого отношения. Как только, такие параметры определенны можно начать статистическую обработку данных и построить модель явления. Но данная модель будет лишь показывать зависимость (корреляцию) выбранных входных параметров от выходных, которые имели место в прошлом.
Минский пытался показать, что перцептрон не имеет в этом отношении серьезных преймуществ по сравнению с другими статистическими методами прогноза. И если рассматривать конечный результат он полностью прав. Единственно, разницу составляет то, что классические статистические методы требуют расчета многих сложных уравнений, а перцептрон более естественно решает требуемые уравнения, что связано с его устройством. Если на перцептрон посмотреть глазами математика, то окажется, что перцептрон это по сути способ решения систем уравнений с большим числом неизвестных коэффициентов. Алгоритм поиска этих коэффициетов технически более быстрый чем у аналогичных классических способов решения уравнений.
Построив систему уравнений, охватывающую наиболее значимые параметры (если нам повезет их найти), можно говорит о том, что мы нашли закон, по статусу близкий к законам физики, но только оперирующий большим числом переменных. Именно такие модели позволяют описывать системы с больщим числом состояний — биологические, социальные и т. п. Именно в этом смысле мы и можем говорить о прогнозе.
Качественость сделанного прогноза или точность построенной модели зависит от числа знаний, используемых при построении модели. Если мы хотим, чтобы на основании половины всех необходимых знаний модель была способна достроить (спрогнозировать) вторую половину неизвестных нам знаний, то желательно иметь информацию равномерно распределенную по всему пространству возможных состояний. В таком случае перцептрон способен спрогнозировать неизвестные, но близкие к известным результаты с определенной верояностью правильности. В противном же случае, мы имеем как раз ситуацию с необходимость прогнозировать результат задачи «шахматной доски», которая рассматривалась выше. Но тут главное, что выше вопрос был связан с возможностью обучения этой задаче, теперь же идет речь о необходимости достроить по имеющейся информации — недостающую, то есть спрогнозировать. Человек с такой задачей справляется быстро, так как находит определенную аналогию. Для перцептрона (а так-же для ряда других ИНС) данная задача в полной мере слишком сложна. Это связанно с основным ограничением ИНС — невозможность найти инвариант (см. выше), в следствии этого перцептрон работает только как статистическая машина, но не способен самостоятеьно находить инварианты, которые были бы основой для принятия решений.
Технические ограничения по скорости и объему используемой памяти
Минский показал, что задачи, которые в принципе могут быть решены перцептроном, могут потребовать нереально больших времен или нереально большой памяти. Например, для различения некоторых классов объектов коэффициенты части ассоциативных элементов должны быть столь велики, что для хранения их в вычислительной машине потребовался бы больший объем памяти, чем для того, чтобы просто запомнить все конкретные объекты этих двух классов.
См. также
- Дельта-правило
- Искусственная нейронная сеть
- Распознавание образов
- Обобщение понятий
- Ассоциативная память
Примечания
Литература
- Фрэнк Розенблатт Принципы нейродинамики: перцептроны и теория механизмов мозга = Principles of Neurodynamic: perceptrons and the theory of brain mechanisms. — М.: «Мир», 1965.
- М. Минский, С. Пейперт Персептроны = Perceptrons. — М.: «Мир», 1971.
- Ф. Вассерман Нейрокомпьютерная техника: Теория и практика. — М.: «Мир», 1992.
- Саймон Хайкин Нейронные сети: полный курс = Neural Networks: A Comprehensive Foundation. — 2-е изд. — М.: «Вильямс», 2006. — С. 1104. — ISBN 0-13-273350-1
- Raul Rojas Neural Networks - A Systematic Introduction. — Springer-Verlag, Berlin, New-York: 1996. — С. 502 p..