Модель МакКаллока-Питтса

Материал из MachineLearning.

Версия от 20:21, 4 января 2010; Platonova.Elena (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Сравнение работы ЕМ-алгоритма и k-means для смесей с экспоненциальным распределением компонент. (будет в заголовке)

В статье приведены примеры классификации ЕМ-алгоритмом и методом k ближайших соседей двумерной смеси, компоненты которой имеют экспоненциальное распределение.

Содержание

1 Краткое описание исследуемых алгоритмов
- 1.1 ЕМ алгоритм
- 1.2 k-means (k ближайших соседей)
2 Примеры работы
3 Литература

Краткое описание исследуемых алгоритмов

ЕМ алгоритм

Основа EM-алгоритма - предположение, что исследуемое множество данных может быть представлено с помощью линейной комбинации распределений, а цель - оценка параметров распределения, которые максимизируют логарифмическую функцию правдоподобия, используемую в качестве меры качества модели. Пусть рассматривается смесь из $k$ распределений, каждое описывается функцией правдоподобия $p_j(x)$

$p(x) = \sum_{i=1}^k w_jp_j(x)$

$w_j$ - априорная вероятность $j$ -й компоненты. Функции правдоподобия принадлежат параметрическому семейству распределений $\varphi(x; \theta)$ и отличаются только значениями параметра $p_j(x) = \varphi(x; \theta_j)$

Вывод формул для алгоритма

Вход:

$R, M, Delta, L$ – общая длина выборки

Выход:

$\theta = (\omega_1, \omega_2, ..., \omega_k, \theta_1, \theta_2, ..., \theta_k)$ параметры распределения и весы компонент.

Оценка максимального правдоподобия (ОМП) θ

для одно- и двумерного случая экспоненциального распределения.

Необходимо максимизировать

$Q(\Theta) = ln\prod_{i=1}^m p(x_i)=\sum_{i=1}^mln\sum_{j=1}^k\omega_jp_j(x_i) \rightarrow ma\limits_{\Theta}x$

Из Лагранжиана следует:

$\omega_j=\frac{1}m \sum_{i=1}^mg_{ij}$ j=1,...,k

$\frac{\partial L}{\partial\theta_j}=\frac{\partial}{\partial\theta_j}\sum_{i=1}^mg_{ij}lnp_j(x_i)=0,$ j=1,...,k.

С учетом $p_j(x)\equiv \varphi(x, \theta_j) = \theta_j \cdot exp{-\theta_j \cdot x}$ получаем ОМП $\theta$ для экспоненциального закона:

$\frac{\partial}{\partial \theta_j}\sum_{i=1}^mg_{ij}(ln \theta_j - \theta_jx_i)=0$

В одномерном случае:

$\theta_j=\frac{\sum_{i=1}^mg_{ij}}{\sum_{i=1}^mx_ig_{ij}}$

В двумерном случае:

$\theta_{jx}=\frac{\sum_{i=1}^mg_{ij}}{\sum_{i=1}^mx_ig_{ij}}\\\theta_{jy}=\frac{\sum_{i=1}^mg_{ij}}{\sum_{i=1}^my_ig_{ij}}$

k-means (k ближайших соседей)

Метод $K$ ближайших соседей - это метрический алгоритм классификации, основанный на оценивании сходства объектов. Классифицируемый объект относится к тому классу, которому принадлежат ближайшие к нему объекты обучающей выборки.

Постановка задачи

Пусть $X \in \mathbb{R}^n\$ - множество объектов; $Y$ - множество допустимых ответов. Задана обучающая выборка $\{(x_i,y_i)\}_{i=1}^\ell$ . Задано множество объектов $\ X^m =\{x_i\}_{i=1}^m$ . Требуется найти множество ответов $\{y_i\}_{i=1}^m$ для объектов $\{x_i\}_{i=1}^m$ .

На множестве объектов задается некоторая функция расстояния, в данном случае $\rho(x,x')$ - максимум модулей

$\rho(x,x') = \max_{i} |x_i-x'_i|;$

Для произвольного объекта $x\in X$ расположим объекты обучающей выборки $x_i$ в порядке возрастания расстояний до $x$ :

$\rho(x,x_{1; x}) \leq \rho(x,x_{2; x}) \leq \cdots \leq \rho(x,x_{m; x}),$

где через $x_{i; x}$ обозначается тот объект обучающей выборки, который является $i$ -м соседом объекта $x$ . Аналогично для ответа на $i$ -м соседе: $y_{i; x}$ .

Таким образом, произвольный объект $x$ порождает свою перенумерацию выборки. В наиболее общем виде алгоритм ближайших соседей есть

$a(x) = \mathrm{arg}\max_{y\in Y} \sum_{i=1}^m \bigl[ x_{i; x}=y \bigr] w(i,x),$

где $w(i,x)$ — заданная весовая функция, которая оценивает степень важности $i$ -го соседа для классификации объекта $u$ .

В рассматриваемом примере $w(i,x) = [i\leq k] ,$ что соответствует методу $k$ ближайших соседей.

Примеры работы

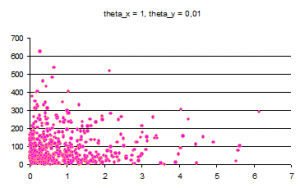
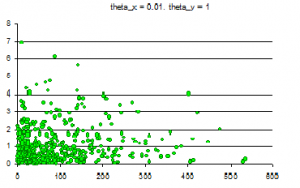
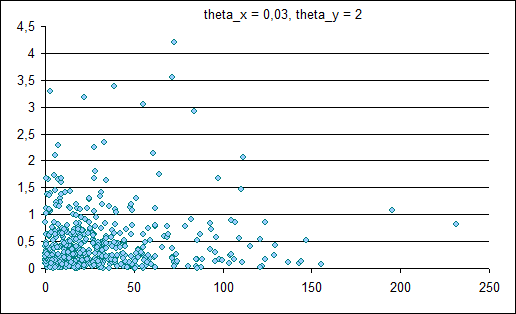
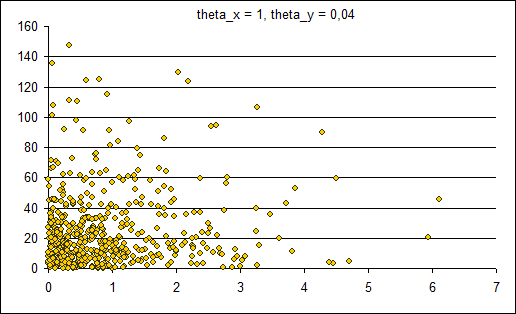
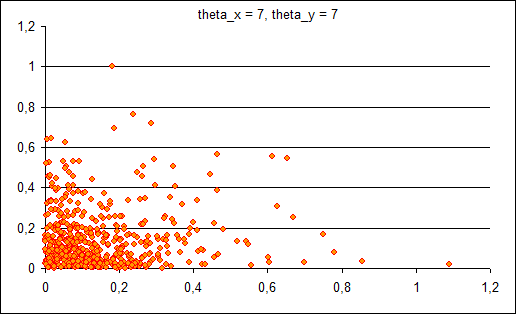
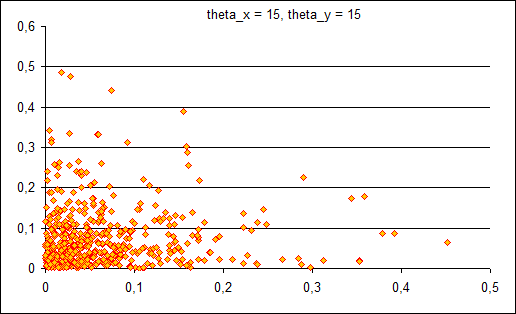
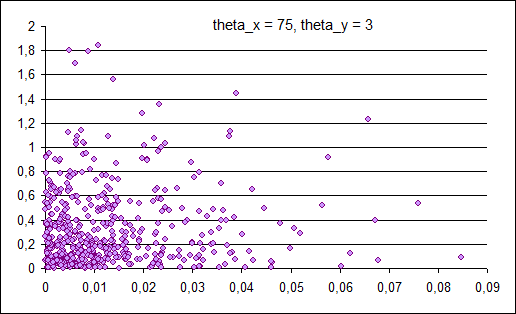
Сравнение проводилось с использованием написанных на практикуме алгоритмов EM и k-means. На графиках, отображающих компоненты, показано по одной из-за большого разброса предельных значений классифицируемых объектов. Следует обратить внимание на интервал, содержащий всю выборку.

Пример №1 (две компоненты)

Смесь из двух компонент по 500 элементов.

$\theta_x=1, \theta_y=0,01$

$\theta_x=0,01, \theta_y=1$

В результате работы ЕМ-алгоритма с последовательным добавлением компонент с параметрами R = 30, M = 20, Delta = 0,001 восстанавливается $\theta_1 = (1.01831, 0.0101044)$ , $\theta_2=(0.0104461, 0.917726)$

Количество ошибок при классификации:

ЕМ 1 из 500 (0.2%)

k-means (k=1) 0 из 500

k-means (k=5) 1 из 500 (0.2%)

Пример №2 (три компоненты)

Смесь из трех компонент по 500 элементов

В результате работы ЕМ-алгоритма с последовательным добавлением компонент с параметрами R = 30, M = 40, Delta = 0,001 восстанавливается

$\theta_1 = (0.0309435, 2.05189)$ ,

$\theta_2=(1.05747, 0.0394895)$ ,

$\theta_3=(6.56629, 6.79212)$

Количество ошибок при классификации:

ЕМ 6 из 500 (1.2%)

k-means (k=1) 12 из 500 (2.2%)

k-means (k=5) 18 из 500 (3.6%)

Пример №3 (четыре компоненты)

Смесь из четырех компонент по 500 элементов. Добавлена компонента с $\theta_x=15,\theta_y=15$

В результате работы ЕМ-алгоритма с последовательным добавлением компонент с параметрами R = 15, M = 30, Delta = 0,001 восстанавливается

$\theta_1 = (0.0300939, 1.96699)$ ,

$\theta_2=(1.02279, 0.041855)$ ,

$\theta_3=(6.1976, 6.23407)$ ,

$\theta_4=(14.8266, 12.9193)$

Количество ошибок при классификации:

ЕМ 37 из 500 (7.4%)

k-means (k=1) 9 из 500 (1.8%)

k-means (k=5) 26 из 500 (5.2%)

Пример №4 (пять компонент)

Смесь из пяти компонент по 500 элементов. Добавили компоненту с $\theta_x=75,\theta_y=3$

В результате работы ЕМ-алгоритма с последовательным добавлением компонент с параметрами R = 7, M = 20, Delta = 0,001 восстанавливается

$\theta_1 = (0.0311774, 1.88446)$ ,

$\theta_2=(1.00218, 0.0372523)$ ,

$\theta_3=(5.9531, 6.10164)$ ,

$\theta_4=(14.6564, 13.2964)$ ,

$\theta_5 = (81.433, 3.10389)$ ,

Количество ошибок при классификации:

ЕМ 243 из 500 (48.6%)

k-means (k=1) 35 из 500 (7%)

k-means (k=5) 22 из 500 (4.2%)

Литература

К. В. Воронцов, Лекции по статистическим (байесовским) алгоритмам классификации
Королёв В.Ю. ЕМ-алгоритм, его модификации и их применение к задаче разделения смесей вероятностных распределений. Теоретический обзор. - М.: ИПИРАН, 2007
http://en.wikipedia.org/wiki/Maximum_likelihood#Discrete_distribution.2C_finite_parameter_space
http://home.dei.polimi.it/matteucc/Clustering/tutorial_html/AppletKM.html
http://www.basegroup.ru/library/analysis/clusterization/em/
http://fedc.wiwi.hu-berlin.de/xplore/ebooks/html/csa/node45.html

Данная статья является непроверенным учебным заданием.

Студент: Участник:Platonova.Elena

Преподаватель: Участник:Константин Воронцов

Срок: 6 января 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://recognition.su/wiki/index.php?title=%D0%9C%D0%BE%D0%B4%D0%B5%D0%BB%D1%8C_%D0%9C%D0%B0%D0%BA%D0%9A%D0%B0%D0%BB%D0%BB%D0%BE%D0%BA%D0%B0-%D0%9F%D0%B8%D1%82%D1%82%D1%81%D0%B0»

Категория: Непроверенные учебные задания

Модель МакКаллока-Питтса

Материал из MachineLearning.

Содержание

Краткое описание исследуемых алгоритмов

ЕМ алгоритм

k-means (k ближайших соседей)

Примеры работы

Пример №1 (две компоненты)

Пример №2 (три компоненты)

Пример №3 (четыре компоненты)

Пример №4 (пять компонент)

Литература

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты