Участник:Vitsemgol/Парадоксы биномиального распределения

Материал из MachineLearning.

< Участник:Vitsemgol

Версия от 11:54, 6 июля 2015; Vitsemgol (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Перейти к: навигация, поиск

{{{1}}}

Содержание

1 История
2 Парадокс 20-го века: Распределение Бернулли и биномиальное распределение — это одно и тоже и каждое из них — распределение одной случайной величины в последовательности независимых испытаний
3 Парадокс первого десятилетия 21-го века: Биномиальное распределение — распределение одной случайной величины в конечной последовательности испытаний Бернулли
4 Парадокс второго десятилетия 21-го века: Биномиальное распределение — распределение одной случайной величины, содержащей ровно успешно завершившихся испытаний Бернулли
- 4.1 Парадокс 20-го века. Математическое ожидание биномиального распределения не равно np
5 Биномиальное распределение как задача разделения дискретного целого на две составные части
- 5.1 Биномиальное распределение как процесс выполнения взаимосвязанных действий над объектами
- 5.2 Биномиальное распределение как простейшая цепь Маркова
6 Наиболее интересные этапы становлнения биномиального и мультиномиального распределений
7 Заключение
8 Литература
9 См.также

История

"История теории вероятности содержит очень много неожиданных парадоксов. По мнению Карла Пирсона, в математике нет другого такого раздела науки, в котором так же легко совершить ошибку": см. Биномиальное распределение – 1.doc; http://gendocs.ru/v1345/Биномиальное распределение. (МИНИСТЕРСТВО РФ ПО СВЯЗИ И ИНФОРМАТИЗАЦИИ. РЕФЕРАТ по дисциплине : «Теория вероятностей» на тему: «Биномиальное распределение» Выполнил: студентка группы АБ-87 Нецветаев Т.М. Новосибирск, 2010); http://www.vixri.ru/d/Sekej%20G.%20_Paradoksy%20v%20teorii%20verojatnostej_.pdf (Секей Габор. Парадоксы в теории вероятностей и математической статистике. Будапешт, 1988. 215 С. Цитата на С. 10).

Биномиальное и полиномиальное (мультиномиальное) распределения зарождались в первой половине XIX века, когда руководящей философской идеей развития теории вероятностей было убеждение во всеобщности понятия независимости. Авторы того времени, вплоть до конца XIX века, как правило, не оговаривали это предположение ^[3].

Известны были только условно независимые (неравновозможные) события. Если “…встречались не все равновозможны, - пояснял В. Я. Буняковский - то чрез дробление на другие, оне могут быть приведены к равновозможным…” ^[4].

С появлением цепей Маркова в начале XX века (1906-1907), к сожалению, не была пересмотрена концепция этих распределений.

Парадокс 20-го века: Распределение Бернулли и биномиальное распределение — это одно и тоже и каждое из них — распределение одной случайной величины в последовательности независимых испытаний

<< БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, распределение Бернулли ^[5], — распределение вероятностей случайной величины $X$ с целочисленными значениями $m=0,1, \ldots,n$ , заданное формулой

$p_m=P(X=m) =C_n^mp^m (1-p)^{n-m}$

где $n\ge1$ и $0\le p\le 1$ — параметры, а $C_n^m$ — биномиальный коэффициент (отсюда название Б. р. ). Б. р. — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний; это — распределение вероятностей числа наступлений некоторого события (<<удачи>> ) в $n$ повторных независимых испытаниях, если при каждом испытании вероятность наступления этого события равна $p$ (см. Бернулли испытания). В соответствии с этим каждую случайную величину $X$ , имеющую Б. р. с параметрами $n$ и $p$ можно представить в виде суммы $n$ независимых случайных величин, имеющих Б. р. с параметрами $n=1$ и $p$ . Математическое ожидание и дисперсия случайной величины $X$ с Б. р. равны $EX=np$ и $DX=np(1-p)$ . Многомерным обобщением Б. р. служит полиномиальное распределение. >> Конец цитаты. Эти распределения аналогично описаны и в Большой Российской энциклопедии ^[6]. В начале 21-го века стало известно, что распределение Бернулли — это самостоятельное распределение в последовательности независимых испытаний. Оно почти одинаково описано в трёх электронных энциклопедиях Викизнание, Наука и Математика: Случайная величина $X$ имеет распределение Бернулли, если она принимает всего два значения: $1$ и $0$ с вероятностями $p$ и $q\equiv 1-p$ соответственно. Таким образом:

$\mathbb{P}(X=1) = p$ ,

$\mathbb{P}(X=0) = q$ .

Схема Бернулли стала известна и впервые была описана в энциклопедии Математика: Последовательность $\{X_n\}_{n=1}^{\infty}$ независимых случайных величин, имеющих распределение Бернулли, называется схемой Бернулли. Физически схема Бернулли моделирует многократное проведение независимых реализаций одного и того же случайного эксперимента с двумя исходами: успех и неудача. Случайное событие $\{X_i=1\}$ соответствует успеху в результате $i$ -го испытания, а событие $\{X_i=0\}$ соответствует неудаче ( http://ru.math.wikia.com/wiki/распределение Бернулли). Тем не менее, и в 21-ом веке можно встретить устаревшие суждения, подобные этому: http://wiki.bks-tv.ru/wiki/Обсуждение: Биномиальное_ распределение: Формула биномиального распределения и формула Бернулли - это одно и то же или нет? -- 10:41, 14 июня 2008 (UTC) Да.109.161.126.71 10:59, 8 ноября 2010 (UTC)

Парадокс первого десятилетия 21-го века: Биномиальное распределение — распределение одной случайной величины в конечной последовательности испытаний Бернулли

Во всех областях научного знания за исключением теории вероятностей приставка би (в переводе с латинского означающая сдвоенный, состоящий из двух частей) используется правильно, например, в авиации биплан — самолет со сдвоенными крыльями, в оптике бинокль — сдвоенный монокль, в комбинаторике бином — двучлен, и только в современной теории вероятностей биномиальное распределение — распределение, полученное не основе бинома (двучлена), является распределением одной случайной величины…

Парадокс заключается в том, что http://wikipedia.ru/wiki/биномиальное распределение традиционной интерпретации 20-го века признаётся распределением одной случайной величины, а на самом деле биномиальное распределение является распределением двух случайных величин, в котором первая случайная величина является независимой, а вторая зависима от первой.

Этот парадокс возник из-за ошибки в логике рассуждений и получил повсеместное распространение с середины 20-го века.

Подобно тому, как из полинома (из многочлена) методом дедукции получают бином (двучлен), а из бинома методом индукции получают полином, так и по аналогии из полиномиального распределения (из мультиномиального распределения с числом случайных величин больше двух) методом дедукции обязаны получить биномиальное распределение (распределение с двумя случайными величинами), а из биномиального распределения (из распределения с двумя случайными величинами) методом индукции обязаны получить полиномиальное распределение (распределение с числом случайных величин больше двух).

Этот парадокс настолько распространён и настолько прост, что может быть проиллюстрирован на элементарных примерах. 1. Пусть в полиноме 10 членов. Сократив в нём число членов до двух, получим два:10:5=2.

2. В биноме 2 члена. Умножив их на 5, получим, что в полиноме 10 членов: 2х5=10.

3. Пусть в полиномиальном распределении 10 случайных величин. Сократив число случайных величин до двух, по аналогии обязаны получить биномиальное распределение с двумя случайными величинами: 10:5=2. Однако принято считать, что биномиальное распределение это распределение одной случайной величины, иными словами, если 10 разделить на 5, то получится один! Это первый парадоксальный результат: 10:5=1.

4. Число случайных величин биномиального распределения традиционной интерпретации, равное одному, умножив на 5 получим, что в полиномиальном распределении 5 случайных величин: 1х5=5. Это второй парадоксальный результат, поскольку изначально исходили из того, что в полиномиальном распределении 10 случайных величин.

Во времена В. Я. Буняковского биномиальное распределение, как распределение двух случайных величин и на его основе полиномиальное распределение (оба так ещё не называемые) впервые были опубликованы им в 1846 году [2].

В современной записи биномиальное и полиномиальное распределения Буняковского имеют следующий вид:

$P(X_1=n_1, X_2=n_2)= \frac{n!}{n_1! n_2!} p_1^{n_1}p_2^{n_2},$

$2=k \le n< \infty, \quad n_1+n_2=n, \quad p_1+p_2=1;$

$P(X_1=n_1,\ldots,X_k=n_k)=\frac{n!}{n_1!\cdots n_k!}p_1^{n_1}\cdots p_k^{n_k},$

$2\le k \le n < \infty,\quad n_1+\ldots+n_k=n.$

Парадокс второго десятилетия 21-го века: Биномиальное распределение — распределение одной случайной величины, содержащей ровно 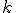$k$ успешно завершившихся испытаний Бернулли

См., например, Галанов Ю. И. Биномиальное распределение и его предельные формы http://hm.tpu.ru/geologi/galanov/lab_mathstat/lb1/bin0.htm 29 Биномиальное распределение -YouTube http://www.youtube.com/watch?v=vKOCLpNt1vM Изучение биномиального распределения - Exponennta.ru http://www.exponenta.ru/educat/systemat/shelomovsky/lab/lab03.asp Биномиальное распределение и его аппроксимация http://ofim.oscsbras.ru/~klokov/probability/simulations/approx.htm Ровно $k$ означает только $k$ и ни чего иного: ни больше, ни меньше, ни $n-k$ неудачно завершённых испытаний, о чём подробно было рассмотрено в предыдущем парадоксе. Не биномиальное распределение, а распределение Пуассона определяет ровно $k$ прошедших событий, причём параметр, определяющий среднее значение $\lambda=pn$ , это ни что иное как математическое ожидание первой случайной величины биномиального распределения! Если в последовательности $n$ испытаний Бернулли $k$ испытаний окончилось успешно с вероятностью $p_1$ каждого, а $n-k$ испытаний в той же последовательности окончилось неудачно с вероятностью $p_2, \quad p_1+p_2=1$ каждого, то вероятность того, что $k$ испытаний окончилось успешно, равна числу сочетаний ${n \choose k}$ из $n$ по $k$ , умноженному на $p_1$ вероятность $k$ успешно окончившегося одного испытания, возведённую в степень $k$ числа уснешно завершённых испытаний: ${n\choose k}p_1^k$ . И это есть ни что иное, как вероятность $P_1( X_1=n_1)$ первой случайной величины, распределения двух случайных величин. Аналогично, если в той же последовательности $n$ испытаний Бернулли $n-k$ испытаний окончилось неудачно с вероятностью $p_2, \quad p_1+p_2=1$ каждого, то вероятность того, что $n-k$ из $n-k$ испытаний окончились неудачно равна числу сочетаний из $n-k$ по $n-k$ ${n-k \choose n-k}=1$ , умноженному на вероятность $p_2$ неудачно окончившегося испытания, возведённую в степень $n-k$ числа неудачно завершённых испытаний: $p_2^{(n-k)}$ . Это есть $P_2(X_2=n_2)$ вероятность второй случайной величины биномиального распределения. Произведение вероятностей первой и второй случайных величин есть вероятность биномиального распределения — распределения двух случайных величин. Зависимость второй от первой случайной величины будет показана ниже. Здесь же главное то, что $p_1n$ это математическое ожидание $P_1( X_1=n_1)$ первой случайной величины биномиального распределения — распределения двух случайных величин. Математическое ожидание $p_1n$ определяет равно $k$ успешно окончившихся испытаний в последовательности $n$ испытаний Бернулли. И эта величина аналогична $\lambda=pn$ в распределении Пуассона, которая определяет среднее значение (ровно $k$ событий) случайной величины.

Парадокс 20-го века. Математическое ожидание биномиального распределения не равно np

Если утверждается, что биномиальное распределение — распределение одной случайной величины и что математическое ожидание этого биномиального распределения есть ни что иное, как

$\mathbf{E}\xi = np,$

где n — число независимых испытаний, а p — вероятность положительного исхода одного испытания, то при увеличении числа испытаний до $n>\frac{1}{p}$

математическое ожидание биномиального распределения окажется больше единицы, что не допустимо, ибо согласно второй аксиоме вероятностей аксиоматики Колмогорова, вероятности всех случайных величин, включая и его математическое ожидание, обязано быть равным единице.

Биномиальное распределение как задача разделения дискретного целого на две составные части

Разделение дискретного целого на две составные части случайного объёма осуществляют в последовательные моменты времени. Дискретное целое $n, \quad 2\le n <\infty$ — множество дискретных элементов. Элементы различимы между собой хотя бы одним признаком и не упорядочены (хаотично расположены). Разделение множества на два подмножества осуществляют методом выбора без возвращения — выбранные элементы множества не возвращают во множество до полного его разделения (изъятия из него элементов). Выбор произвольного элемента множества равновероятен и равен $p_i=n^{-1}, \quad i=1,\ldots,n$ . В начальный момент времени $t_0$ , не обязательно равный нулю $t_0 \ne 0$ , множество содержит $n, 2\le n < \infty$ различимых неупорядоченных элементов. В первый момент времени $t_1,\quad t_1>t_0$ из исходного множества, содержащего $n, \quad 2\le n<\infty$ элементов, осуществляют выборку случайного объёма $n_1, \quad 0\le n_1\le n$ элементов множества. Вероятность первой случайной величины $X_1$ , принявшей в первый момент времени $t_1$ числовое значение $n_1$ , равна числу сочетаний ${n \choose n_1}$ из $n$ по $n_1$ , умноженному на вероятность выбора одного элемента $p_1=n^{-1}$ , возведённого в степень $n_1$ — числа выбранных элементов

$P_1(t_1,X_1=n_1)={n \choose n_1}p_1^{n_1}.$

Во второй момент времени $t_2\quad t_2>t_1$ вторая случайная величина $X_2$ вынуждена принять единственно возможное значение $n_2=n-n_1$ , поскольку в первый момент времени $t_1$ первая случайная величина $X_1$ приняла числовое значение $n_1$ . Условная вероятность второй случайной величины $P_2(t_2,X_2=n_2 \mid t_1,X_1=n_1)$ равна числу сочетаний ${n-n_1 \choose n_2=n-n_1}= {n-n_1 \choose n-n_1}=1$ из $n-n_1$ по $n_2=n-n_1$ , умноженному на вероятность выбора одного элемента $p_2=n^{-1}$ , возведённого в степень $n_2$ — числа выбранных элементов

$P_2(t_2,X_2=n_2 \mid t_1,X_1=n_1)=p_2^{n_2}.$

Произведение вероятностей первой и второй случайных величин есть вероятность биномиального распределения Таким образом, биномиальное распределение — это распределение двух случайных величин, в котором первая случайная величина является действительно независимой, а вторая зависима от первой.

Биномиальное распределение как процесс выполнения взаимосвязанных действий над объектами

Объекты: множество, его подмножества и их элементы как объективная реальность, существующая вне нас и независимо от нас. Биномиальное распределение это:

случайный процесс безвозвратного разделения последовательно во времени $t_1,\quad t_2$ и в пространстве конечного $n$ - множества различимых неупорядоченных элементов на две части $n_1, \quad n_2$ случайных объёмов, сумма которых равна объёму исходного множества: $n_1+ n_2=n, \quad 2\le n<\infty$ ,
разделение множества осуществляют выборками без возвращения (изъятые из множества элементы не возвращают обратно во множество до полного окончания экспериментов),
вероятность попадания одного произвольного элемента множества в каждое из подмножеств $0\le p_i<1, \quad i=1,2$ принимают за вероятность успеха (успешного завершения испытания) распределения Бернулли,
вероятности успехов Бернулли распределения нормируют $\sum _{i=1}^2 p_i =1$ согласно аксиоматике Колмогорова,
очерёдность следования выборок принимают за нумерацию случайных величин биномиального распределения,
случайный объём каждой выборки $n_i, \quad i=1,2$ в момент времени $t_i, \quad i=1,2$ принимают за числовое значение соответствующей случайной величины $X_i=n_i, \quad i=1,2$ биномиального распределения,
результаты каждого разбиения обрабатывают вероятностными методами, определяют технические характеристике всех выборок и принимают их за технические характеристики случайных величин биномиального распределения,
минимально необходимый набор технических характеристик случайных величин и биномиального распределения в целом это: пространство элементарных событий, вероятность , математическое ожидание и дисперсия,
математическое ожидание биномиального распределения имеет место, когда число выборок $k$ равно числу элементов $n$ -множества $k=n$ и численно равно $\frac{n!}{n^n}=\frac{2!}{2^2}=\frac{1}{2}$ .

Биномиальное распределение как простейшая цепь Маркова

Биномиальное распределение появляется в последовательности двух испытаний, первое из них случайное независимое, а второе зависимое от первого испытания. Исходы испытаний конечны и счётны. По сути — это простейшая цепь Маркова. ( $X_0$ , называемое начальным распределением цепи Маркова, для биномиального распределения не имеет смысла $t_0=0, \quad X_0=0$ , поскольку нумерация случайных величин начинается с единицы.) Единственная переходная вероятность заключается в том, что вторая случайная величина $X_2$ во второй момент времени $t_2$ вынуждена принять числовое значение, равное $0\le n_2=n-n_1$ , при условии, что в первый момент времени $t_1$ первая случайная величина $X_1$ приняла случайное число $0\le n_1\le n$ . Следовательно и вероятность биномиального распределения

$\prod_{i=1}^2P(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=\frac{n!}{n_1! n_2!}p_1^{n_1}p_2^{n_2}$

как произведение первой независимой и второй зависимой случайных величин является цепью Маркова. Сумма вероятностей биномиального распределения равна единице. Следовательно, биномиальное распределение как цепь Маркова, является стахостической.

Переходная вероятность биномиального распределения является дискретной функцией. Следовательно, биномиальное распределение является марковским процессом с дискретным временем.

Наиболее интересные этапы становлнения биномиального и мультиномиального распределений

Начальный этап становления биномиального распределения

Зарождение биномиальное распределение зарождалось как комбинаторная задача на основе разложения бинома $(a + b)^n$

Принцип полной индукции восходит к древним грекам, например, к “Началам” Евклида, а в странах ислама формула бинома $(a + b)^n$ при $n=3,4,\ldots,9$ была известна уже в 10-12 веках таким учёным, как: Ат-Туси, Ал-Каши и Омар Хайям.

Первый из них (Абу Джафар Мухаммад ибн Мухаммад Насир ад-Дин ат-Туси) Ат-Туси (1201- 26 июня 1274) уроженец города Туса в Хорасане, работал сначала в столице государства ассасинов. Ат-Туси принадлежит много трудов по математике и астрономии, а также по физике, минералогии, логике, этике и другим наукам. ^[7]

В «Сборнике по арифметике с помощью доски и пыли» (1265) Ат-Туси подробно описал приём извлечения корней любой степени и привел таблицу биномиальных коэффициентов в форме треугольника, известного ныне как треугольник Паскаля ^[8].

Последний из них владел правилом возведения двучлена в любую целую положительную степень. Однако эти сочинения Хайяма пока не найдены. Но на их существование говорит его цитата: “Мы покажем, как определить основания квадрато–квадратов, квадрато–кубов, кубов–кубов и так далее сколько угодно, чего раньше не было”. По-видимому, эти общие результаты в словесном изложении не дошли в своё время до Европы, и здесь пришлось их получать заново .

Первая половина 19-го века - дальнейшее теоретическое и практическое применение бинома Ньютона в теории вероятностей

Процитируем ^[9] и проанализируем урновую модель Лапласа: <<Предположим, что урна содержит $a$ белых и $b$ черных шаров, и что по изъятии из неё шара, его кладут обратно в урну: спрашивается, какова вероятность того, что при $n$ тиражах будут вынуты $m$ белых шаров и $n-m$ черных. Ясно, что число случаев возможных при каждом тираже равно $a$ плюс $b$ . Так как каждый случай второго тиража может комбинироваться со всеми случаями первого, то число случаев возможных при двух тиражах, равно квадрату бинома $a$ плюс $b$ . В разложении этого квадрата квадрат $a$ выражает число случаев, в которых два раза вынут белый шар, удвоенное произведение $a$ на $b$ выражает число случаев, в которых вынуты белый и черный шары; наконец, квадрат $b$ выражает число случаев, в которых вынуты два черных шара. Продолжая таким образом дальше, находят вообще, что $n$ -я степень бинома $a$ плюс $b$ выражает число всех случаев возможных при $n$ тиражах, и что в разложении этой степени член, умноженный на $m$ -ю степень $a$ выражает число случаев, в которых можно вынуть $m$ белых шаров и $n-m$ черных. Поэтому, деля этот член на всю степень бинома, получим вероятность изъятия $m$ белых шаров и $n-m$ черных. Так как отношения $a$ и $a$ плюс $b$ есть вероятность изъятия белого шара, а отношение $b$ и $a$ плюс $b$ есть вероятность изъятия черного шара, если при этом назовем эти вероятности $p$ и $q$ , то вероятностью изъятия $m$ белых шаров при $n$ тиражах будет член, умноженный на -ю степень , в разложении $n$ -й степени бинома $p$ плюс $q$ : легко заметить, что сумма $p$ плюс $q$ есть единица. Это замечательное свойство бинома оказывается очень полезным в теории вероятностей>>.

Примечания. 1. В современной теории вероятностей тиражом называют одно независимое повторное испытание с двумя несовместными исходами каждый (испытание Бернулли), что в модели Лапласа, например, означает: “успешный исход” случайного события $A=1$ — вынут белый шар, “неудачный исход” случайного события $A=0$ — вынут черный шар.

2. Процедура изъятия из урны одного произвольного шара и каждый раз возвращение его в урну до следующего изъятия со времён Лапласа закрепилась в теории вероятностей как метод выбора с возвращением получения бинома и вероятностей биномиального распределения (ещё так не называемого).

3. Возникли существенные различия биномиальных распределений, полученных на основе двух рассмотренных биномов $a$ плюс $b$ в степени $n$ и $p$ плюс $q$ в степени $n$ , связанных одним тождеством

$\frac{(a+b)^n}{(a+b)^n}=1^n=(p+q)^n, \qquad p=\frac{a}{a+b}, \qquad q= \frac{b}{a+b}.$

Из дроби $\frac{(a+b)^n}{(a+b)^n}$ Лаплас определил вероятность биномиального распределения как вероятность изъятия $m$ белых шаров и $n-m$ черных:

$P(a=m,b=n-m)= \frac {{n\choose m}a^mb^{n-m}}{(a+b)^n},$

а из бинома $(p+q)^n$ — вероятность биномиального распределения как вероятность изъятия $m$ только белых шаров

$P(a=m)= {n\choose m}p^mq^{n-m}.$

В России в 1846 году В. Я. Буняковский на основе комбинаций исходов независимых испытаний получил вероятность биномиального распределения, как распределения двух случайных величин ^[10] . Однако это осталось незамеченным возможно потому, что Буняковский опубликовал свою работу только на русском языке и в очень ограниченном количестве экземпляров. А при жизни Лапласа его трактат был опубликован пять раз: в феврале и ноябре 1814, 1816, 1819 и 1825 годах. Кроме того, в последствии трактат и его переводы неоднократно переиздавались во многих странах вплоть до конца XX века. В США последний раз был переиздан в 1994 году, а в России — в 1999 году в составе энциклопедии.

Опыт философии в теории вероятностей ^[11] — образец гениальности Лапласа. Он изложил полную теорию на то время, привел полный свод истин из теории вероятностей и приложений анализа вероятностей без применения формул и сложных вычислений.

В первой половине 19-го века В. Я. Буняковский назвал труд Лапласа бессмертным творением утверждая, что никому аналитическая Теория Вероятностей не обязана столько, как Лапласу.

Только в начале 20-го века появились первые критические высказывания в адрес трактата Лапласа, вспоминал Г. Крамер полвека спустя ^[12]

Видимо сказался авторитет Лапласа, и, как следствие, многие столетия развитие биномиального распределения шло в направлении распределения одной случайной величины.

В СССР, даже в середине 20-го века эта точка зрения не ставилась под сомнение. В качестве примера процитируем вышедший в 1956 году в Издательстве АН СССР 3-томный коллективный труд “Математика, ее содержание, методы и значения”. В нём говорится, что глава XI — Теория вероятностей — из 2-го тома этого труда, написанная академиком А. Н. Колмогоровым , до наших дней сохраняет интерес для представителей естественнонаучных и инженерных специальностей, учителей математики ^[13].

Цитируем из неё с несущественными изменениями обозначений: <<Вычислим теперь вероятность $P_k$ ровно $k$ появлений некоторого события $A$ в $n$ независимых испытаниях, в каждом из которых вероятность $p$ этого события одна и та же.

Обозначим через $\vee$ событие, заключающееся в непоявлении события $A$ .

Очевидно, что

$P(\vee)=1-P(A)=1-p.$

Из независимости испытаний нетрудно усмотреть, что вероятность какой-либо определенной последовательности, составленной из $k$ появлений $A$ и $n-k$ непоявлений, равна

$p^k(1-p)^{n-k}.$

Так, например, при $n=5$ и $k=2$ вероятность получить последовательность исходов будет

$p(1-p)p(1-p)(1-p) =p^2(1-p)^3.$

По теореме сложения вероятность $P_k$ равна сумме вероятностей всех последовательностей с $k$ появлений и с $n-k$ непоявлений события $A$ , т. е. в силу

$p^k(1-p)^{n-k}$

равна произведению числа таких последовательностей на $p^k(1-p)^{n-k}$ . Число таких последовательностей, очевидно, равно числу сочетаний из $n$ по $k$ , поскольку $k$ положительных исходов могут занимать в ряду $n$ испытаний любые $k$ мест.

Окончательно получаем

$P_k= C_n^kp^k(1-p)^{n-k} \qquad (k=0,\ldots,n).$

(так наз. биномиальное распределение) >> Конец цитаты.

Проанализируем получение Колмогоровым биномиального распределения.

Во-первых, была поставлена задача вычислить вероятность ровно $k$ появлений одного и того же случайного события в последовательности, содержащей $n$ независимых испытаний.

Во-вторых, в процессе решения поставленной задачи дополнительно была вычислена вероятность ровно $n-k$ появлений и второго случайного события в той же последовательности, а именно, вероятность непоявления первого случайного события. Иными словами, была вычислена совместная вероятность появления двух случайных событий на едином пространстве элементарных событий, представляющем собой последовательность $n$ независимых испытаний.

И, наконец, в-третьих, произведение вероятности ровно $k$ появлений одного и вероятности ровно $n-k$ непоявлений другого случайного события было принято за вероятность ровно $k$ появлений первого случайного события в последовательности независимых испытаний:

$P_k= C_n^kp^k(1-p) ^{n-k} \qquad (k=0,\ldots,n).$

По Колмогорову так называемое биномиальное распределение есть распределение одной случайной величины, появляющейся ровно $k$ раз, причём эта точка зрения существует и в настоящее время.

Однако не биномиальное распределение, как утверждает Колмогоров, а распределение Пуассона

$P_k=e^{-\lambda}\frac{\lambda^k}{k!},$

в котором $\lambda=np$ , на самом деле определяет вероятность ровно $k$ появлений того же случайного события в последовательности $n$ независимых испытаний ^[14], причем параметр $\lambda=np$ есть математическое ожидание первой случайной величины биномиального распределения (и полиномиального распределения тоже) настоящей интерпретации.

В. Я. Буняковский в 1846 году первым в мире получил формулу вероятности биномиального распределения как распределения двух случайных величин. В ту пору не были известными многие современные математические знаки такие, как суммирование, произведение, факториал и другие. В современной записи Биномиальное распределение Буняковского выглядит следующим образом:

$P(X_1=n_1, X_2=n_2)= \frac{n!}{n_1! n_2!} p_1^{n_1}p_2^{n_2},$

$2=k \le n< \infty, \quad n_1+n_2=n, \quad p_1+p_2=1.$

В том же 1846 году В. Я. Буняковский методом индукции распространил математическую формулу разложения бинома “на случай сколь угодно большого числа событий”, тем самым получил новое тождество

$\frac{(a+b+c+\ldots)^n}{(a+b+c+\ldots)^n }=1^n=(p_1+p_2+p_3+\ldots)^n,$

в котором

$\frac{a}{a+b+c+\ldots}, \quad \frac{b}{a+b+c+\ldots}, \quad \frac{c}{a+b+c+\ldots},$

из которого В. Я. Буняковский первым в мире получил и формулу вероятности полиномиального распределения традиционной интерпретации (независимых случайных величин).

В современной записи Мультиномиальное распределение независимых случайных величин (Мультиномиальное распределение Буняковского) выглядит следующим образом:

$P(X_1=n_1,\ldots,X_k=n_k)=\frac{n!}{n_1!\cdots n_k!}p_1^{n_1}\cdots p_k^{n_k},$

$2\le k \le n< \infty, \quad n_1+\ldots+n_k=n, \quad p_1+ \ldots +p_ k =1.$

Заключение

По числу парадоксов (3) биномиальное распределение уступает только мультиномиальному (полиномиальному) распределению (как минимум 5). Главные причины возникновения парадоксов — ошибки в логике и в методе его получения. В частности, биномиальное не потому что его формула содержит биномиальные коэффициенты, а потому что оно первоначально было получено из бинома (двучлена), именно поэтому обязано быть распределением двух случайных величин, о чём было известно В. Я. Буняковскому ещё 1846 году! Это же почти доказал и Лаплас в 1812 году ^[15], ^[16].

Новое — это хорошо забытое старое.

На самом деле биномиальное распределение получают в процессе разбиения множества различимых и неупорядоченных элементов на два подмножества случайных объёмов, в сумме составляющих исходное множество. Число подмножеств равно числу случайных величин распределения. Процесс разбиения множества осуществляют последовательно во времени методом выбора без возвращения .

Главным распространителем парадоксов биномиального и мультиномиального распределений является Википедия, которая нарушает заодно и свои правила ВП МАРГ: http://ru.wikipedia.org/wiki/Биномиальное распределение и http://ru.wikipedia.org/wiki/Мультиномиальное распределение (не представлен ни один авторитетный источник). Если в мультиномиальном распределении (https://ru.wikipedia.org/wiki/Multinomial_distribinion) сократить число случайных величин до двух (к=2) (см. в оригинале это выглядит так: When k = 2, the multinomial distribution is the binomial distribution), то получим биномиальное распределение https://en.wikipedia.org/wiki/Binomial_distribution. Так сколько в биномиальном распределении случайных величин? Две или одна? По логике и по приведённым рассуждениям, естественно, напрашивается ответ, что две. Однако согласно энциклопедии Википедии биномиальное распределение содержит одну случайную величину. Это же явный парадокс. Именно с этим парадоксом я и борюсь с августа 2012 года!

Пришло время, когда биномиальное распределение и мультиномиальное распределение описаны на единой методологической основе:

методом индукции от биномиального распределения приходим к мультиномиальному;

методом дедукции от мультиномиального распределения приходим к биномиальному.

Если и найдётся человек-чудак, который всерьёз будет утверждать, что << биномиальное распределение — это распределение одной случайной величины, полученное методом выбора с возвращением >>, поприветствуем его как человека из прошлого века.

Литература

↑ Буняковский В. Я. ОСНОВАНИЯ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ВЕРОЯТНОСТЕЙ сочинение В. Я. БУНЯКОВСКОГО, ИМПЕРАТОРСКОЙ АКАДЕМИИ НАУК, ОРДИНАРНОГО АКАДЕМИКА, ПРОФЕССОРА С. ПЕТЕРБУРГСКОГО УНИВЕРСИТЕТА, ДОКТОРА МАТЕМАТИЧЕСКИХ НАУК ПАРИЖСКОЙ АКАДЕМИИ. САНКТПЕТЕРБУРГ. В Типографии Императорской Академии Наук. 1846. 477 с.
↑ Феллер В. Введение в теорию вероятностей и ее приложения. Том 1, перевод с англ. М.: Мир, 1984, 528с.
↑ История математики, т. 2. Математика XV11 века. М.: Наука, 1970, 300 С.
↑ Буняковский В. Я. ОСНОВАНИЯ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ВЕРОЯТНОСТЕЙ сочинение В. Я. БУНЯКОВСКОГО, ИМПЕРАТОРСКОЙ АКАДЕМИИ НАУК, ОРДИНАРНОГО АКАДЕМИКА, ПРОФЕССОРА С. ПЕТЕРБУРГСКОГО УНИВЕРСИТЕТА, ДОКТОРА МАТЕМАТИЧЕСКИХ НАУК ПАРИЖСКОЙ АКАДЕМИИ. САНКТПЕТЕРБУРГ. В Типографии Императорской Академии Наук. 1846. 477 с.
↑ Биномиальное распределение. Математический энциклопедический словарь. / Гл. ред. Ю. В Прохоров; Ред. кол. С. И. Адян, Н. С. Бахвалов, В. И. Батюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. - М.: Сов. энциклопедия, 1988. С.95.
↑ Большев Л. Н. Биномиальное распределение. Вероятность и математическая статистика: Энциклопедия / Гл. ред. Ю. В. Прохоров.- М.: Большая Российская энциклопедия, 1999. С. 49-50. ISBN 5-85270-265-X
↑ История математики. Том 1. С древних времён до начала нового времени. М.: Наука, 1970. 351 с.
↑ http://wikipedia.ru/wiki/Математика исламского средневековья
↑ Вероятность и математическая статистика: Энциклопедия / Гл. ред. Ю. В. Прохоров, 1999. - 910 с. ISBN 585270265X
↑ Буняковский В. Я. Основания математической теории вероятностей. Сочинение Императорской Академии Наук ординарного академика, профессора С.Петербургского университета и доктора математических наук Парижской Академии. САНКТПЕТЕРБУРГ, Типография Императорской Академии Наук. СПб. 1846. 477 с.
↑ Laplace P. Essai philosophique sur les probabilités. Paris, 1812. (Опыт философии теории вероятностей). Пер. с фр. A.I.B., под ред. А. К. Власова, М.: Московский университет, 1908.
↑ Крамер Г. Полвека с теорией вероятностей: наброски воспоминаний. Современные проблемы математики. М.: Знание. 1979. 60 с.
↑ Математика, её содержание, методы и значения Том. 2.М. АН СССР. 1956.
↑ Феллер В. Введение в теорию вероятностей и её приложения. Том 1. перевод с англ. М.: Мир, 1984. 528 с. C. 173
↑ Laplace P. Essai philosophique sur les probabilités. Paris, 1812. (Опыт философии теории вероятностей). Пер. с фр. A.I.B., под ред. А. К. Власова, М.: Московский университет, 1908.
↑ Лаплас П. Опыт философии теории вероятностей. // Вероятность и математическая статистика: Энциклопедия. М.: Большая Российская энциклопедия, 1999. С. 834-863. ISBN 585270265X

См.также

Источник — «http://recognition.su/wiki/index.php?title=%D0%A3%D1%87%D0%B0%D1%81%D1%82%D0%BD%D0%B8%D0%BA:Vitsemgol/%D0%9F%D0%B0%D1%80%D0%B0%D0%B4%D0%BE%D0%BA%D1%81%D1%8B_%D0%B1%D0%B8%D0%BD%D0%BE%D0%BC%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B3%D0%BE_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F»

Категория: Вероятностные распределения