Комбинаторная теория переобучения (виртуальный семинар)

Материал из MachineLearning.

Версия от 14:49, 19 декабря 2010; Vokov (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Перейти к: навигация, поиск

Содержание

1 Оценки обобщающей способности: история вопроса
2 Как были выявлены эффекты расслоения и сходства
3 Оценки расслоения–связности
4 Точные оценки вероятности переобучения
5 Методы получения точных оценок переобучения
6 Литература
7 См. также

Данный виртуальный семинар предназначен для обсуждения

эффектов расслоения и сходства в семействах алгоритмов классификации;
влияния этих эффектов на обобщающую способность;
математических техник, позволяющих учитывать эти эффекты в оценках вероятности переобучения.

Оценки обобщающей способности: история вопроса

Точные оценки вероятности переобучения необходимы для создания методов обучения по прецедентам, гарантирующих высокое качество классификации новых объектов, не вошедших в обучающую выборку. Получение точных оценок обобщающей способности остаётся открытой проблемой в теории статистического обучения уже более 40 лет, начиная с VC-теории, предложенной В. Н. Вапником и А. Я. Червоненкисом. Наиболее точные из известных оценок всё ещё сильно завышены.

VC-теория

Основной задачей в VC-теории считается получение верхних оценок для функционала

$P_\varepsilon(A) = \mathbb{P}_X\Bigl( \sup_{a\in A} |P(a)-\nu(a,X)| \geq \varepsilon \Bigr),$

где

$A$ — семейство алгоритмов, из которого по обучающей выборке $X$ выбирается некоторый алгоритм;

$P(a)$ — вероятность ошибки алгоритма $a \in A$ ;

$\nu(a,X)$ — частота ошибок алгоритма $a \in A$ на независимой обучающей выборке длины $\ell$ ;

$\mathbb{P}_X$ — некоторая неизвестная вероятностная мера на множестве объектов.

Смысл этого функционала в том, что если частота ошибок не сильно отклоняется от вероятности ошибки одновременно для всех алгоритмов $a \in A$ , то алгоритм, найденный путём минимизации эмпирического риска,

$a^{*} = \arg\min_{a\in A} \nu(a,X),$

будет иметь малую вероятность ошибиться и на новых данных, иными словами, будет иметь хорошую обобщающую способность.

Это утверждение записывают также в эквивалентном виде:

«Для любого $a \in A$ с вероятностью не менее $1-\eta$ выполняется $P(a) \leq \nu(a,X)+\varepsilon(\eta)$ »,

где $\varepsilon(\eta)$ — функция, обратная к $\eta(\varepsilon) = P_\varepsilon(A)$ .

У функционала $P_\varepsilon$ есть несколько недостатков.

Если вероятностная мера $P(a)$ неизвестна, то измерить функционал $P_\varepsilon$ непосредственно в эксперименте очень трудно, поскольку невозможно идентифицировать наступление события
$\sup_{a\in A} |P(a)-\nu(a,X)| \geq \varepsilon.$
Экспериментальное измерение необходимо для количественного анализа и понимания причин завышенности оценок функционала $P_\varepsilon$ . Выход заключается в том, чтобы вместо $P(a)$ оценивать $\nu(a,\bar X)$ — частоту ошибок алгоритма $a$ на независимой контрольной выборке длины $k$ . Тогда эмпирическое измерение функционала $P_\varepsilon$ становится возможным, например, методом Монте-Карло — путём генерации некоторого числа случайных разбиений полной выбоки $X^L = X \sqcup \bar X$ на обучение и контроль. Через $L=\ell+k$ обозначается длина полной выборки.

Супремум в VC-теории вводится для того, чтобы получить наиболее общую оценку, не зависящую от конкретного метода обучения $\mu$ , который по обучающей выборке $X$ находит алгоритм $a\in A$ . Однако на самом деле было бы правильнее оценивать вероятность переобучения — события
$\delta_\mu(X) = \nu(\mu(X),\bar X)-\nu(\mu(X),X) \geq \varepsilon$ ,
где величина $\delta_\mu(X)$ называется переобученностью. Введение супремума приводит к верхней оценке вероятности переобучения. Эта оценка может оказаться сильно завышенной, поскольку при решении прикладных задач методы обучения возвращают не любые алгоритмы из $A$ , а лишь те, которые в определённом смысле «похожи» на восстанавливаемую зависимость.

Наконец, имеет смысл оценивать сверху саму переобученность, а не её абсолютную величину, поскольку частоту ошибок на контрольной выборке хотелось бы ограничивать именно сверху, а не снизу.

Понятие вероятности переобучения

Наиболее адекватным функционалом обобщающей способности является вероятность переобучения:

$Q_\varepsilon(\mu,X^L) = \mathbb{P}\Bigl[ \delta_\mu(X) \geq \varepsilon \Bigr].$

Этот функционал является локальной оценкой обобщающей способности, поскольку он зависит от метода обучения и полной выборки.

Термин переобучение понимается здесь в строго формальном смысле, как событие $\delta_\mu(X) \geq \varepsilon$ .

Вероятность $\mathbb{P}$ понимается здесь и далее в смысле равномерного распределения на множестве всех $C_L^\ell$ разбиений неслучайной полной выбоки $X^L = X \sqcup \bar X$ . Это позволяет применять чисто комбинаторные методы для получения оценок вероятности переобучения, и во многих случаях получать точные оценки (не завышенные, не асимптотические). См. также слабая вероятностная аксиоматика.

Основным объектом изучения в комбинаторно-дискретной постановке является бинарная матрица ошибок $I = (I_{id})$ размера $L{\times}D$ . Строки матрицы соотвествуют объектам полной выборки, столбцы — алгоритмам, значение $I_{id}=1$ означает, что алгоритм $a_d$ допускает ошибку на объекте $x_i$ . Столбец этой матрицы называется вектором ошибок алгоритма $a_d$ . Предполагается, что все векторы ошибок различны. Число столбцов $D$ в матрице ошибок называется также коэффициентом разнообразия (shattering coefficient) семейства алгоритмов.

Комбинаторная оценка для одного алгоритма

Если множество алгоритмов состоит из единственного элемента, $A=\{a\}$ , то именно он и возвращается методом обучения при любой обучающей выборке. Собственно, никакого обучения нет. Этот случай интересен тем, что вероятность переобучения выражается через гипергеометрическое распределение и является точной.

Теорема (one-classifier bound, OC-bound). Для любого алгоритма $a$ , любой выборки $X^L$ и любого $\varepsilon\in(0,1)$

$Q_\varepsilon(a,X^L) = H_L^{\ell,m} \bigl( \frac{\ell}{L}(m-\varepsilon k) \bigr),$

где

$m = n(a,X^L)$ — число ошибок алгоритма $a$ на полной выборке;

$H_L^{\ell,m}(s) = \sum_{t=0}^{\lfloor s \rfloor}\frac{C_m^s C_{L-m}^{\ell-t}}{C_L^\ell}$ — функция гипергеометрического распределения.

Эта оценка является аналогом закона больших чисел в слабой вероятностной аксиоматике.

Эта оценка является «строительным блоком» для более сложных случаев, когда метод обучения выбирает алгоритм из множества $A$ .

Эта оценка является ненаблюдаемой, поскольку правая часть зависит от числа ошибок на контрольной выборке, которая скрыта в момент обучения. Однако, зная число ошибок на обучающей выборке $s = n(a,X)$ , нетрудно построить доверительный интервал для неизвестной величины $m$ .

Комбинаторная VC-оценка

Оценка для общего случая получается путём суммирования OC-оценок по всему семейству.

Теорема (Vapnik-Chervonenkis bound, VC-bound). Для любого семейства $A$ , любого метода обучения $\mu$ , любой выборки $X^L$ и любого $\varepsilon\in(0,1)$

$Q_\varepsilon(\mu,X^L) = \sum_{a\in A} H_L^{\ell,m} \bigl( \frac{\ell}{L}(m-\varepsilon k) \bigr),$

где

$m = n(a,X^L)$ — число ошибок алгоритма $a$ на полной выборке;

$H_L^{\ell,m}(s)$ — функция гипергеометрического распределения.

Доказательство состоит из двух шагов, на каждом из которых происходит существенная потеря точности оценки.

Шаг 1. Вероятность переобучения оценивается сверху вероятностью большого равномерного отклонения частот (uniform bound). В результате получаем оценку, справедливую для любого метода обучения $\mu$ .

$Q_\varepsilon(\mu,X^L) = \mathbb{P} \Bigl[ \delta_\mu(X) \geq \varepsilon \Bigr] \;\leq\; \tilde Q_\varepsilon(A,X^L) = \mathbb{P} \max_{a\in A} \Bigl[ \delta_a(X) \geq \varepsilon \Bigr].$

Шаг 2. Максимум бинарных величин оценивается сверху их суммой. Или, что то же самое, вероятность объединения событий оценивается сверху суммой их вероятностей. Это называется неравенством Буля или union bound:

$\tilde Q_\varepsilon(A,X^L) \leq \sum_{a\in A} \mathbb{P} \Bigl[ \delta_a(X) \geq \varepsilon \Bigr].$

Теперь остаётся применить OC-оценку под знаком суммы. Теорема доказана.

Чтобы получить VC-оценку в классической записи, необходимо положить $\ell=k$ и сделать ещё два чисто технических огрубления: во-первых, оценить сверху функцию гипергеометрического распределения при наихудшем $m$ ; во-вторых, применить асимптотическую оценку для левого хвоста гипергеометрического распределения.

Следствие

$Q_\varepsilon(\mu,X^L) \leq |A| \cdot \exp(-\ell^2\varepsilon).$

Эта оценка является сильно завышенной. Она справедлива для любой восстанавливаемой зависимости, любой выборки и любого метода обучения. Следовательно, это оценка худшего случая. Примерно понятно, что есть «худший случай» — когда никакой зависимости в данных нет, а метод обучения настолько глуп, что выбирает алгоритм наугад. Очевидно, худший случай не интересен, и на практике никогда не реализуется.

Правая часть VC-оценки зависит только от размерных характеристик матрицы ошибок $L$ и $D=|A|$ , но не от её содержимого. Этих величин явно недостаточно, чтобы характеризовать столь сложный процесс, как обучение по прецедентам. В этом и заключается основная концептуальная причина завышенности классических VC-оценок.

Развитие теории вычислительного обучения

Последующие работы были направлены на получение более точных оценок, учитывающих больше априорной информации, позволяющих управлять процессом обучения.

Теория равномерной сходимости [Вапник, Червоненкис, 1968]
Корректные алгебры ограниченной ёмкости [Матросов, 1980]
Theory of learnable (PAC-learning) [Valiant, 1982]
Data-dependent bounds [Haussler, 1992]
Concentration inequalities [Talagrand, 1995]
Connected function classes [Sill, 1995]
Similar classifiers VC bounds [Bax, 1997]
Margin based bounds [Bartlett, 1998]
Self-bounding learning algorithms [Freund, 1998]
Rademacher complexity [Koltchinskii, 1998]
Adaptive microchoice bounds [Langford, Blum, 2001]
Algorithmic stability [Bousquet, Elisseeff, 2002]
Algorithmic luckiness [Herbrich, Williamson, 2002]
Shell bounds [Langford, 2002]
PAC-Bayes bounds [McAllester, 1999; Langford, 2005]

Как были выявлены эффекты расслоения и сходства

В комбинаторном подходе оцениваемый функционал $Q_\varepsilon$ легко измерить эмпирически методом Монте-Карло, взяв среднее по некоторому случайному подмножеству разбиений полной выборке на две подвыборки, обучающую и контрольную. Более того, можно оценить и промежуточные величины, которые появляются в ходе вывода VC-оценки, и узнать, какова потеря точности на каждом шаге. Заметим, что ничего подобного в исходной вероятностной постановке сделать нельзя, так как функционал $P_\varepsilon(A)$ с трудом поддаётся эмпирическому измерению. Методика измерения была предложена Вапником и Ботту (1994), однако эти работы остались практически незамеченными, что не удивительно: измеренные значения этого функционала близки к единице, в силу завышенности равномерной оценки (uniform bound). Содержательные эксперименты стали возможны только после того, как VC-оценки были переписаны в слабой вероятностной аксиоматике для вероятности переобучения, которая легко измеряется эмпирически.

Первый эксперимент (на реальных данных)

В экспериментах на реальных задачах классификации удалось количественно оценить отдельные факторы завышенности классических VC-оценок.

Основные причины завышенности, в порядке убывания важности:

Пренебрежение эффектом расслоения (или локализации) семейства алгоритмов. Чем хуже классификатор решает данную задачу, тем меньше шансов получить его в результате настройки по обучающей выборке. Это означает, что реально работает не всё семейство, а только какая-то его часть, своя в каждой задаче.
Степень завышенности: порядка $10^2..10^5$ , в зависимости от задачи.
Пренебрежение эффектом сходства алгоритмов. При выводе классических VC-оценок используется неравенство Буля (union bound) — оценка вероятности объединения событий суммой их вероятностей. Эта оценка становится чрезвычайно завышенной, если среди алгоритмов есть похожие.
Степень завышенности: порядка $10^3..10^4$ . Этот фактор всегда существенен и не так сильно зависит от задачи, как первый.
Экспоненциальная аппроксимация хвоста гипергеометрического распределения. Вроде бы точность аппроксимации увеличивается с ростом длины выборки — хвосты быстро стремятся к нулю. Однако относительная погрешность (отношение аппроксимированного значения к точному) с ростом выборки растёт! Отсюда вывод: при получении численно точных оценок не стоит пользоваться аппроксимациями.
Степень завышенности: порядка $10^0..10^2$ .

В экспериментах вычислялся также эффективный локальный коэффициент разнообразия (ЭЛКР). Это такое число $D$ , при котором VC-оценка не была бы завышенной. Для него были получены удивительно небольшие значения — порядка $10^0..10^2$ в разных задачах, в то время как число $D$ имело порядки $10^6..10^{12}$ .

Основные выводы:

Завышенность VC-оценок обусловлена тем, что они учитывают только длину выборки $L$ и число различных алгоритмов $D$ , но не учитывают степень их различности, то есть полностью игнорируют содержимое матрицы ошибок.
Для получения точных оценок необходимо одновременно учесть оба эффекта — и расслоение, и сходство.
Ни одна из существовавших до сих пор теорий не в состоянии объяснить столь низких значений эффективного коэффициента разнообразия.

Второй эксперимент (на модельных данных)

Зависимость $Q_\varepsilon(D)$ для четырёх семейств при $\ell=k=100,\; \varepsilon=0.05,\; m_0=10$ ; число разбиений в методе Монте-Карло — 10000;
[+Ц] — цепочка, [+Р] — с расслоением,
[-Ц] — не-цепочка, [-Р] — без расслоения.

Простейшим примером семейства алгоритмов с расслоением и связностью является монотонная цепочка алгоритмов. Оно строится следующим образом. Задаётся «лучший алгоритм», допускающий $m_0$ ошибок на полной выборке. Каждый следующий алгоритм $a_{d+1}$ допускает ошибки на тех же объектах, что и предыдущий $a_{d}$ , плюс ошибку ещё на одном объекте. Перестановкой строк можно добиться, чтобы матрица ошибок такого семейства содержала верхнюю треугольную подматрицу.

Монотонная цепочка алгоритмов является довольно реалистичной моделью связного семейства с одним непрерывным параметром: чем дальше значение параметра от оптимального значения, тем больше ошибок, но в силу непрерывности (и при гипотезе, что выборка находится «в общем положении») ошибка не может появиться сразу на нескольких объектах. Вообще, связным семейством будем называть такое множество алгоритмов, в котором для каждого алгоритма найдётся другой алгоритм, вектор ошибок которого отличается от данного только на одном объекте.

Монотонной цепочке можно поставить в соотвествие цепочку без расслоения. В этом семействе каждый следующий алгоритм также отличается от предыдущего только на одном объекте, но число ошибок, чередуясь, принимает лишь два значения: $m_0, m_0+1$ .

Каждому из этих двух семейств можно сопоставить не-цепочку. Чтобы разрушить эффект связности, достаточно в каждом столбце матрицы ошибок случайным образом переставить все элементы.

Итак, получается четыре модельных семейства, заданных непосредственно своими маатрицами ошибок. Для каждого из них вероятность переобучения нетрудно оценить методом Монте-Карло (у хороших студентов реализация такого экспериментального стенда занимает обычно около пары часов работы). Результаты сопоставляются на графиках зависимости вероятности переобучения $Q_\varepsilon$ от числа $D$ первых алгоритмов $a_1,\ldots,a_D$ , из которых метод обучения $\mu(X)$ выбирает алгоритм с наименьшей частотой ошибок на обучающей выборке. В VC-теории такой метод обучения называется минимизацией эмпирического риска.

Основные выводы:

Связность заметно снижает темп роста зависимости $Q_\varepsilon(D)$ .
Расслоение понижает уровень горизонтальной асимптоты $Q_\varepsilon(D)$ .
Только при одновременном наличии и связности, и расслоения вероятность переобучения приемлемо мала, причём кривая «выходит на насыщение» после первых 5–7 алгоритмов. Основная масса «плохих» алгоритмов вообще не вносит вклад в переобучение.
При отсутствии либо расслоения, либо связности переобучение наступает уже при нескольких десятках алгоритмов.
Это означает, что реальные семейства, состоящие из огромного числа различных алгоритмов, с необходимостью должны быть расслоенными и связными.
Семейство без расслоения и без связности — это и есть тот наихудший случай, который изучается в VC-теории.

Этот эксперимент показал направление дальнейших исследований: для получения точных оценок вероятности переобучения необходимо развивать методы, одновременно учитывающие эффекты расслоения и сходства в семействе алгоритмов.

О природе переобучения

Вообще, переобучение возникает из-за того, что решение о выборе лучшего алгоритма принимается по неполным данным — обучающей выборке $X$ , которая является лишь частью полной выборки $X^L$ .

Сделаем мысленный эксперимент. Представим, что все алгоритмы семейства имеют одинаковую вероятность ошибок. Тогда число ошибок на конечной выборке подчиняется биномиальному распределению, имеющему форму пика. Шансы отдельному алгоритму угодить в левый хвост распределения невелики. Однако чем больше алгоритмов мы будем брать, тем дальше влево будет смещаться минимальное (по всем взятым алгоритмам) число ошибок; тем больше будет разность между частотой и вероятностью ошибок у «лучшего» алгоритма. Это и есть переобучение.

Это всё так, если алгоритмы берутся из распределения случайно и независимо. Однако, если алгоритмы зависимы, то возникает надежда, что выбираемые алгоритмы будут концентрироваться гуще, и пик эмпирического распределения числа ошибок окажется более узким. В реальной ситуации алгоритмы зависимы, причём очень сильно, благодаря свойствам расслоения и сходства.

Оценки расслоения–связности

Свойство расслоения

Определение. Расслоением семейства алгоритмов $A$ называется его разбиение на непересекающиеся подмножества — слои:

$A = A_0 \sqcup A_1 \sqcup \dots \sqcup A_L,$

где $m$ -й слой есть подмножество алгоритмов с $m$ ошибками на полной выборке:

$A_m = \bigl\{ a\in A:\: n(a,X^L)=m \bigr\}.$

Определение. Неоптимальностью $r(a)$ алгоритма $a\in A$ называется число объектов, на которых данный алгоритм допускает ошибку, таких, что существует другой алгоритм, не допускающий ошибки на данном объекте и на объектах, на которых не ошибается алгоритм $a\in A$ .

Используемые на практике семейства алгоритмов, как правило, универсальны, то есть предназначены для решения очень широкого класса задач. Однако нас интересует решение лишь одной фиксированной задачи, в частности, восстановление конкретной функциональной зависимости $y(x)$ по выборке прецедентов $X=\bigl\{(x_i,y_i=y(x_i)):\: i=1,\ldots,\ell\bigr\}$ . При фиксированной целевой зависимости $y(x)$ подавляющее большинство алгоритмов допускают слишком много ошибок. Они практически никогда не будут выбираться методом обучения, каков бы ни был состав объектов $x_i,\: i=1,\ldots,\ell$ в обучающей выборке. Эффективно работают лишь алгоритмы из нескольких нижних слоёв, остальная часть семейства фактически остаётся незадействованной.

Свойство связности

Определение. Верхней связностью $q(a)$ алгоритма $a\in A$ называется число алгоритмов в следующем слое, вектор ошибок которых отличается от $a$ только на одном объекте.

Определение. Нижней связностью $p(a)$ алгоритма $a\in A$ называется число алгоритмов в предыдущем слое, вектор ошибок которых отличается от $a$ только на одном объекте.

Многие параметрические семейства алгоритмов обладают следующим свойством: при изменении вектора параметров по некоторой непрерывной траектории каждое изменение вектора ошибок происходит только на одном объекте. Одновременное изменение нескольких координат возможно, но только для «редких» траекторий, образующих в пространстве траекторий множество меры нуль. В частности, этим свойством обладают классификаторы с непрерывной по параметрам разделяющей поверхностью: линейные классификаторы, SVM с непрерывными ядрами, нейронные сети с непрерывными функциями активации, решающие деревья с пороговыми условиями ветвления, и многие другие. J. Sill называет такие семейства связными, так как множество векторов ошибок всех алгоритмов семейства представляется в виде связного графа. E. Bax предлагает кластеризовать семейство на группы схожих классификаторов.

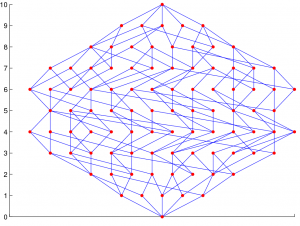
Граф расслоения-связности

Определение. Графом расслоения-связности семейства алгоритмов $A$ называется граф, вершины которого соответствуют векторам ошибок; рёбрами соединяются векторы ошибок, отличающиеся только на одном объекте (хэммингово расстояние между которыми равно 1). Этот граф можно рассматривать как ориентированный, если договориться, что рёбра направлены от алгоритмов с меньшим числом ошибок к алгоритмам с большим числом ошибок.

Граф расслоения-связности зависит от семейства алгоритмов и от конкретной выборки.

Пример. На следующих рисунках показан начальный фрагмент матрицы ошибок (три нижних слоя) и граф расслоения-связности, порождаемые семейством линейных классификаторов на выборке из 10 объектов, по 5 объектов в каждом классе.

0-й слой (1 корректный алгоритм):	1-й слой (5 алгоритмов):	2-й слой (8 алгоритмов):

Матрица ошибок:	Граф расслоения-связности:

Эксперименты с линейными классификаторами проведены Ильёй Решетняком.

Оценки расслоения-связности

Теорема (splitting and connectivity bound, SC-bound). Если $\mu$ — метод минимизации эмпирического риска, то для любой выборки $X^L$ и любого $\varepsilon\in(0,1)$ справедлива оценка сверху:

$Q_\varepsilon(\mu,X^L) \;\leq\; \sum_{a\in A} W_{rq} H_{L-q-r}^{\ell-q,\,m-r}\Bigl(\frac{\ell}{L}(m-\varepsilon k)\Bigr),$

$\mathbb{P}\bigl[ \mu(X)=a \bigr] \;\leq\; W_{rq} = \frac{C_{L-q-r}^{\ell-q}}{C_{L}^{\ell}},$

где

$q=q(a)$ — верхняя связность алгоритма $a$ ;

$r=r(a)$ — неоптимальность алгоритма $a$ ;

$m=n(a,X^L)$ — число ошибок на полной выборке алгоритма $a$ ;

$H_L^{\ell,m}(s)$ — функция гипергеометрического распределения.

Эта оценка является взвешенной суммой OC-оценок с весами $W_{rq}$ , имеющими следующие свойства:

вес $W_{rq}=1$ при $r=q=0$ ; это означает, что если пренебречь расслоением и связностью, то SC-оценка перейдёт непосредственно в VC-оценку;
вес $W_{rq}$ является верхней оценкой вероятности того, что алгоритм будет получен в результате обучения по случайной обучающей подвыборке;
вес $W_{rq}$ убывает экспоненциально по $r$ и по $q$ .

Отсюда вытекают два главных вывода:

чем сильнее связность, тем меньше вероятность переобучения;
основной вклад в вероятность переобучения вносят нижние слои.

Нижние слои содержат, как правило, очень малую долю алгоритмов. Поэтому можно надеяться, что перебор алгоритмов из нижних слоёв позволит достаточно эффективно вычислять SC-оценки.

Точные оценки вероятности переобучения

Точные оценки вероятности переобучения в настоящее время удалось получить для ряда модельных семейств алгоритмов. Все эти семейства являются «искусственными» в том смысле, что они задаются непосредственно бинарной матрицей ошибок, а не каким-либо реальным семейством алгоритмов и реальной выборкой. В некоторых случаях удаётся строить примеры выборок, для которых порождаются именно такие матрицы ошибок. Однако число этих случаев исчезающе мало в сравнении с числом всевозможных матриц, порождаемых реальными задачами обучения. Все модельные семейства отличаются некоторой «регулярностью» или симметрией, которой, как правило, не обладают реальные семейства. Тем не менее, изучение модельных семейств представляется перспективным по нескольким причинам.

Во-первых, они хорошо иллюстрируют эффекты расслоения и связности.
Во-вторых, на них отрабатываются математические приёмы, которые могут оказаться полезными при получении оценок более общего вида.
В-третьих, рассмотрение большого числа разнообразных частных случаев ведёт к постепенному обобщению модельных семейств и получению оценок, неплохо аппроксимирующих вероятность переобучения реальных семейств. Такой путь развития комбинаторной теории переобучения представляется наиболее реалистичным.
Наконец, это просто интересные задачки по комбинаторике.

Пара алгоритмов

Множество алгоритмов состоит из двух элементов, $A=\{a_1,a_2\}$ . Задаётся три параметра:

$m_1$ — число объектов полной выборки, на которых только $a_1$ допускает ошибку;

$m_2$ — число объектов полной выборки, на которых только $a_2$ допускает ошибку;

$m_0$ — число объектов полной выборки, на которых оба алгоритма допускают ошибку.

Это первый частный случай, для которого была получена точная комбинаторная оценка вероятности переобучения. Оценка доказывается путём довольно элементарных комбинаторных рассуждений.

Оценка зависит от ненаблюдаемых параметров $m_0,m_1,m_2$ . Зная соотвествующие три величины на обучающей выборке $s_0,s_1,s_2$ , нетрудно построить доверительную область для неизвестных величин $m_0,m_1,m_2$ .

Основные выводы:

Если два алгоритма почти одинаковы, то переобучения почти нет (эффект сходства).
Если один из двух алгоритмов существенно лучше другого, то переобучения почти нет (эффект расслоения).
Переобучение максимально и достигает VC-оценки только когда алгоритмы максимально плохи (каждый допускает ошибки на половине объектов) и максимально различны.

Монотонная цепочка алгоритмов

Монотонная цепочка алгоритмов является моделью связного семейства с одним непрерывным параметром. Это именно то модельное семейство, которое использовалось во втором эксперименте (см. выше).

Основные выводы:

Монотонная цепочка почти не переобучается
Нескольких алгоритмов с наименьшим числом ошибок уже достаточно, чтобы очень точно вычислить вероятность переобучения монотонной цепочки.

Унимодальная цепочка алгоритмов

Унимодальная цепочка алгоритмов является более реалистичной моделью связного семейства с одним непрерывным параметром, по сравнению с монотонной цепочкой. Представляется естественным, что если непрерывный параметр имеет оптимальное значение, то отклонение от него в обе стороны — как в сторону возрастания, так и в сторону убывания — приводит к росту числа ошибок на полной выборке.

Получение точной оценки для унимодальной цепочки технически гораздо сложнее, чем для монотонной цепочки.

Единичная окрестность лучшего алгоритма

Единичная окрестность лучшего алгоритма — это множество алгоритмов, состоящее из фиксированного алгоритма, называемого «лучшим», и некоторого числа $D$ алгоритмов, допускающих ошибки на тех же объектах, что и «лучший» алгоритм, плюс ещё на каком-то одном объекте.

Связка монотонных цепочек

Это семейство является обобщением трёх предыдущих. Унимодальная цепочка — это связка из двух монотонных цепочек. Единичная окрестность — это связка из $D$ цепочек длины 2.

Точные оценки вероятности переобучения для связки монотонных цепочек получены Александром Фреем.

Слой булева куба

Слой булева куба — это множество всех $C_L^m$ алгоритмов, векторы ошибок которых содержат ровно $m$ единиц. Это пример семейства без расслоения. Оценка вероятности переобучения в этом случае является вырожденной и принимает только значения 0 или 1:

$Q_\varepsilon = \bigl[ \varepsilon k \leq m \leq L-\varepsilon\ell \bigr].$

Интервал булева куба и его расслоение

Интервал булева куба ранга $m$ — это множество алгоритмов, векторы ошибок которых определяются двумя множествами объектов:

$m_0$ «плохих» объектов, на которых все алгоритмы допускают ошибку;

$m$ «пограничных» объектов, на которых алгоритмы данного семейства допускают ошибки всеми возможными $2^m$ способами;

остальные $L-m_0-m$ объектов являются «хорошими»: на них ни один из алгоритмов не допускает ошибок.

Интервал булева куба содержит ровно $2^m$ алгоритмов.

Точная оценка получена как для интервала, так и для $d$ нижних слоёв интервала (это множество из $C_m^0+\cdots+C_m^d$ алгоритмов).

Основные выводы:

Вероятность переобучения очень быстро растёт по $m$ и по $d$ . Доля «пограничных» объектов в выборке практически гарантированно добавляется к величине переобученности.
Гипотеза о существовании пограничного слоя объектов выглядит весьма разумной для задач классификации. Однако в реальных семействах, скорее всего, реализуются далеко не все дихотомии множества пограничных объектов (иначе переобучение было бы слишком велико). Полный интервал булева куба вряд ли может служить адекватной моделью задач с пограничными объектами, а небольшое количество нижних слоёв интервала — вполне может.

Хэммингов шар и его расслоение

Хэммингов шар радиуса $R$ — это множество векторов ошибок, отличающихся от заданного вектора $a_0$ не более чем на $R$ объектах.

Хэммингов шар является моделью максимально плотного связного семейства с расслоением. Слой хэммингова шара (пересечение шара со слоем булева куба) является моделью максимально плотного связного семейства без расслоения. Поэтому оценку вероятности переобучения для слоя шара возможно использовать как нижнюю оценку вероятность переобучения для слоя заданной мощности $|A_m|$ .

Уже самый нижний слой хэммингова шара содержит слишком много алгоритмов, поэтому хэмминговы шаров вряд ли могут служить адекватными моделями нижних слоёв реальных семейств.

Точные оценки вероятности переобучения для хэммингова шара и его слоёв получены Ильёй Толстихиным.

Монотонная многомерная сетка алгоритмов

Монотонная сетка алгоритмов является многомерным обобщением монотонной цепочки алгоритмов. Монотонная $h$ -мерная сетка является моделью связного семейства алгоритмов с $h$ непрерывными параметрами. Есть основания полагать, что нижние слои монотонных сеток могут быть использованы в качестве достаточно адекватных моделей реальных семейств, при надлежащем подборе параметра размерности $h$ .

Точные оценки вероятности переобучения для монотонных и унимодальных многомерных сеток получены Павлом Ботовым.

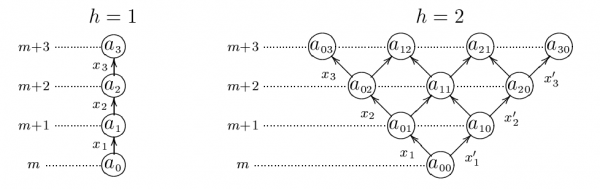
Слева: одномерная монотонная сетка высоты 3 (монотонная цепочка). Справа: двумерная монотонная сетка высоты 3. Горизонтальные линии отмечают слои — число ошибок на полной выборке. Объекты вдоль стрелок означают, что переход от нижнего алгоритма к верхнему связан с появлением ошибки на данном объекте.

Унимодальная многомерная сетка алгоритмов

Унимодальная сетка алгоритмов является более адекватной моделью связного семейства алгоритмов с $h$ непрерывными параметрами. В отличие от монотонной сетки предполагается, что отклонение любого параметра от оптимального значения в обе стороны должно приводить к увеличению числа ошибок.

Вероятность переобучения унимодальной сетки приблизительно равно вероятности переобучения монотонной сетки удвоенной размерности.

Методы получения точных оценок переобучения

Метод порождающих и запрещающих множеств

Метод основан на следующем предположении.

Гипотеза 1. Для любого алгоритма семейства $a\in A$ можно указать порождающее множество объектов $X_a\in X^L$ и запрещающее множество объектов $X'_a\in X^L$ такие, что для любого разбиения полной выборки на обучение и контроль, $X^L = X\sqcup\bar X$ справедливо

$[\mu(X)=a] \;=\; [X_a\in X][X'_a\in \bar X].$

Это предположение справедливо для монотонной цепочки, единичной окрестности и многомерной монотонной сетки. Зная для любого алгоритма $a\in A$ его порождающее и запрещающее множества, можно без труда выписать точные оценки вероятности переобучения, а также $P_a = \mathbb{P}[\mu(X)=a]$ — вероятности того, что данный алгоритм будет выбран в результате обучения.

Для унимодальных цепочек и сеток Гипотеза 1 уже не верна, но верно её обобщение.

Гипотеза 2. Для любого алгоритма семейства $a\in A$ можно указать совокупность $V_a$ пар множеств: порождающие множества объектов $X_{av}\in X^L$ и запрещающие множества объектов $X'_{av}\in X^L$ такие, что для любого разбиения полной выборки на обучение и контроль, $X^L = X\sqcup\bar X$ справедливо

$[\mu(X)=a] \;=\; \sum_{v\in V_a} c_{av}[X_{av}\in X][X'_{av}\in \bar X],$

при некоторых вещественных коэффициентах $c_{av}$ (пока не известны ситуации, когда $c_{av}\neq\pm 1$ ).

Зная для любого алгоритма $a\in A$ все пары порождающих и запрещающих множеств, также можно без труда выписать точные оценки вероятности переобучения, а также вероятности $P_a = \mathbb{P}[\mu(X)=a]$ .

Рекуррентный метод

Рекуррентный метод основан на методе порождающих и запрещающих множеств. Он позволяет вычислять точные оценки вероятности переобучения в том случае, когда семейство $A$ наращивается по одному алгоритму. На каждом шаге в семейство добавляется один алгоритм; для него формируется запрещающее множество (доказывается, что порождающее пусто, и других пар порождающих–запрещающих множеств у него нет); затем для всех предыдущих алгоритмов корректируются пары порождающих–запрещающих множеств. При этом могут возникать новые пары. В некоторых случаях это может приводить к экспоненциальному росту объёма вычислений. Оказывается, что если в этом алгоритме всегда пропускать тот шаг, который может приводить к возникновению новых пар, то будет получена верхняя оценка вероятности переобучения. Оказывается также, что эта оценка не сильно завышена и учитывает граф расслоения-связности.

Теорема. Пусть в $A$ есть алгоритм, не допускающий ошибок на полной выборке. Пусть $\Delta_{mq}$ — профиль расслоения–связности — число алгоритмов в $m$ -м слое со связностью $q$ . Тогда справедлива верхняя оценка вероятности переобучения

$Q_\eps \leq \sum_{m=\lceil \eps k\rceil}^L \sum_{q=0}^L \Delta_{mq} \frac{C_{L-m-q}^{\ell-q}}{C_L^\ell}.$

В этой оценке комбинаторный множитель убывает экспоненциально (быстрее геометрической прогрессии) по $m$ и по $q$ .

Основные выводы:

Только нижние слои графа расслоения–связности могут вносить существенной вклад в вероятность переобучения.
С ростом связности эта оценка улучшается экспоненциально по сравнению с классической VC-оценкой.
Эксперименты показывают, что значения связности концентрируются вблизи размерности пространства параметров. Действительно, связность $q(a)$ — это число способов (степеней свободы), которыми можно «испортить» алгоритм, перейдя от него к другому алгоритму, допускающему ещё на одну ошибку больше.

Открытые проблемы:

Оценка является ненаблюдаемой. Необходимо научиться оценивать профиль расслоения–связности $\Delta_{mq}$ по наблюдаемой обучающей подвыборке $X\subset X^L$ .
Ограничение корректности является техническим и, по всей видимости, его удастся снять.
Обосновать, что эффекты расслоения и связности «практически независимы», то есть что двумерную матрицу профиля расслоения–связности можно с большой точностью представлять в виде произведения одномерных профилей:

$\Delta_{mq} \approx D_m \,\cdot\, \lambda_q,$

где

$D_m = |A_m|$ — профиль расслоения;

$\lambda_q = \frac1{|A|}\left|\bigl\{a\in A:\: q(a)=q \bigr\}\right|$ — профиль связности.

Метод цепных разложений

Метод цепных разложений, предложенный Денисом Кочедыковым, является основным средством получения UC-оценок. Он также позволяет снять ограничение корректности.

Блочный метод

Метод основан на предположении, что в матрице ошибок есть много одинаковых строк, которые объединяются в блоки. Число блоков — это число попарно различных строк. Выписывается точная оценка вероятности переобучения, трудоёмкость вычисления которой экспоненциальна по числу блоков. С помощью этого метода удаётся выписывать вероятность переобучения для произвольных матриц ошибок с небольшим числом столбцов, в частности, для пары и тройки алгоритмов. Однако объём вычислений в общем случае растёт как $O(2^D)$ , и при числе алгоритмов порядка длины выборки использование данного метода практически теряет смысл.

Теоретико-групповой подход

Теоретико-групповой подход, предложенный Александром Фреем, позволяет выписывать точные оценки вероятности переобучения для симметричных семейств алгоритмов и рандомизированного метода обучения. С помощью этой техники получены оценки для связки монотонных цепочек и хэммингова шара.

Неравенства Бонферрони-Галамбоса

Попытки применить неравенства типа Бонферрони для получения оценок вероятности переобучения пока не привели к заметным успехам. Пока единственный результат следующий. Если семейство алгоритмов является связным и в графе расслоения—связности можно выделить полный подграф — дерево, то в оценках Вапника–Червоненкиса «хвост» гипергеометрического распределения можно заменить на значение гипергеометрической вероятности в той же точке. Это даёт несущественное улучшение точности оценки.

Литература

Воронцов, К. В. Комбинаторная теория надёжности обучения по прецедентам: Дис. док. физ.-мат. наук: 05-13-17. — Вычислительный центр РАН, 2010. — 271 с. (подробнее). Презентация на защите (PDF, 1760 КБ).
Воронцов К.В. Открытые проблемы и задачи по спецкурсу «Теория надёжности обучения по прецедентам» (PDF, 180 КБ).
Sill J. Generalization bounds for connected function classes.
Bax E. T. Similar classifiers and VC error bounds: Tech. Rep. CalTech-CS-TR97-14:6 1997.
Langford J. Quantitatively tight sample complexity bounds. — 2002. — Carnegie Mellon Thesis.

См. также

Теория Вапника-Червоненкиса
Слабая вероятностная аксиоматика
Теория надёжности обучения по прецедентам (курс лекций, К.В.Воронцов)
К. В. Воронцов — страница на MachineLearning.RU.
К. В. Воронцов — страница на сайте ВЦ РАН.

Это незавершённая статья о незавершённом исследовании.

Источник — «http://recognition.su/wiki/index.php?title=%D0%9A%D0%BE%D0%BC%D0%B1%D0%B8%D0%BD%D0%B0%D1%82%D0%BE%D1%80%D0%BD%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%BF%D0%B5%D1%80%D0%B5%D0%BE%D0%B1%D1%83%D1%87%D0%B5%D0%BD%D0%B8%D1%8F_%28%D0%B2%D0%B8%D1%80%D1%82%D1%83%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D1%81%D0%B5%D0%BC%D0%B8%D0%BD%D0%B0%D1%80%29»

Категории: Виртуальные семинары | Открытые проблемы и полемика | Теоретические исследования | Теория вычислительного обучения

Комбинаторная теория переобучения (виртуальный семинар)

Материал из MachineLearning.

Содержание

Оценки обобщающей способности: история вопроса

VC-теория

Понятие вероятности переобучения

Комбинаторная оценка для одного алгоритма

Комбинаторная VC-оценка

Развитие теории вычислительного обучения

Как были выявлены эффекты расслоения и сходства

Первый эксперимент (на реальных данных)

Второй эксперимент (на модельных данных)

О природе переобучения

Оценки расслоения–связности

Свойство расслоения

Свойство связности

Граф расслоения-связности

Оценки расслоения-связности

Точные оценки вероятности переобучения

Пара алгоритмов

Монотонная цепочка алгоритмов

Унимодальная цепочка алгоритмов

Единичная окрестность лучшего алгоритма

Связка монотонных цепочек

Слой булева куба

Интервал булева куба и его расслоение

Хэммингов шар и его расслоение

Монотонная многомерная сетка алгоритмов

Унимодальная многомерная сетка алгоритмов

Методы получения точных оценок переобучения

Метод порождающих и запрещающих множеств

Рекуррентный метод

Метод цепных разложений

Блочный метод

Теоретико-групповой подход

Неравенства Бонферрони-Галамбоса

Литература

См. также

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты