Марковский алгоритм кластеризации
Материал из MachineLearning.
(→Марковский алгоритм кластеризации) |
(→Марковский алгоритм кластеризации) |
||
| Строка 4: | Строка 4: | ||
== Марковский алгоритм кластеризации == | == Марковский алгоритм кластеризации == | ||
| - | |||
| Строка 13: | Строка 12: | ||
Данный алгоритм был разработан в рамках PhD работы Van Dongen в 2000 году в центре математических и компьютерных наук в Нидерландах. | Данный алгоритм был разработан в рамках PhD работы Van Dongen в 2000 году в центре математических и компьютерных наук в Нидерландах. | ||
| - | + | ||
| - | + | Термины и определения | |
| - | + | ||
| - | + | Граф состоит из двух типов объектов 1) вершин(узлов)- V | |
| - | + | 2)ребер (пар вершин соединенных между собой) - E. Более формальная запись G:=(V,E) | |
| - | + | ||
| - | + | Кроме этого каждый граф можно представить в виде матрицы смежности (M) размером V*V. Где Mij= растоянию | |
| - | + | между узлом i и узлом j. | |
| - | + | ||
| - | + | Ckexfqyjve j,[jle d uhfat | |
| - | + | ||
| - | # | + | |
| - | + | Что такое кластер в графе? Возможно дать два близких понятия: | |
| - | + | #Длинна пути между узлами одного кластера мало по сравнению с длинно пути между точками пренадлежажащими одному кластеру. | |
| + | #При случайном обходе графа, прежде чем покинуть кластер будут посещены многоие из его вершин | ||
| + | |||
| + | |||
| + | |||
| + | Графы часто возникают при упрощении сложных систем. К примеру в виде графа удобно отображать: | ||
| + | #взамосвязи различных сайтов в интернете | ||
| + | #Социальные сети (сети контактов) | ||
| + | #Генные сети в молекулярной биологии | ||
| + | #порты, аэропорты, города (в качестве узлов графа)и пути их соединяюющие (в качестве ребер). | ||
| + | |||
| + | Следует отметить что случайное блуждание в графе - это конечная цепь Маркова. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | В качестве метрики растояния можно использовать суммы длин ребер (или их количества) между двумя точками, что по сути является евклидовой метрикой. | ||
| + | |||
---- | ---- | ||
| Строка 116: | Строка 132: | ||
14 (1995), pp. 154–162. | 14 (1995), pp. 154–162. | ||
| + | |||
| + | |||
| + | |||
| + | 3.2.1 Приложения | ||
| + | #умножение разреженных матриц (распределения строк по разным процессора), параллельные вычисления, численное решение уравнений в частных производных . | ||
| + | Разреженное матричное умножение требует м. | ||
| + | Минимизация объема связи между процессорами - это разбиение графа | ||
| + | проблема. [A. Gupta, Fast and effective algorithms for graph partitioning and sparsematrix ordering, IBM Journal of Research & Development, 41 (1997). http://www.research.ibm.com/journal/rd/411/gupta.html]. | ||
| + | Решатели PDE действуют на сетке или сетке, и параллельное вычисление такого решателя требует | ||
| + | разделение сетки, опять же, чтобы минимизировать связь между процессами | ||
| + | сорс [53]. | ||
| + | планирование и размещение микросхем [C. J. Alpert and A. B. Kahng, Recent directions in netlist partitioning: a survey, Integration: the VLSI Journal, 19 (1995), pp. 1–81.] | ||
| + | • Оценка требований к проводке и производительности системы в синтезаторе высокого уровня. | ||
| + | Сис и поэтажное планирование. | ||
| + | #На сегодняшний день данный алгоритм применяется для данных в молекулярной биологии (выделение групп генов) [S. Brohee and J. van Helden. Evaluation of clustering algorithms for protein- | ||
| + | protein interaction networks. BMC Bioinformatics, 7, 2006.][J. Vlasblom and S.J. Wodak. Markov clustering versus affinity propagation for the partitioning of protein interaction graphs. BMC bioinformatics, 10(1):99, 2009.] | ||
| + | #анилизе изображений. | ||
Список используемой литературы | Список используемой литературы | ||
Версия 18:06, 12 декабря 2018
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |
Марковский алгоритм кластеризации
Марковский алгоритм кластеризации (MCL, Markov Clustering Algorithm) — алкоритм кластерного анализа основанный на потоке (случайном блуждании) в графе. Изначально разработан для выделения кластеров в графе, однако может быть применен к любым объектам для которых задана матрица сходства/различия.
Данный алгоритм был разработан в рамках PhD работы Van Dongen в 2000 году в центре математических и компьютерных наук в Нидерландах.
Термины и определения
Граф состоит из двух типов объектов 1) вершин(узлов)- V 2)ребер (пар вершин соединенных между собой) - E. Более формальная запись G:=(V,E)
Кроме этого каждый граф можно представить в виде матрицы смежности (M) размером V*V. Где Mij= растоянию между узлом i и узлом j.
Ckexfqyjve j,[jle d uhfat
Что такое кластер в графе? Возможно дать два близких понятия:
- Длинна пути между узлами одного кластера мало по сравнению с длинно пути между точками пренадлежажащими одному кластеру.
- При случайном обходе графа, прежде чем покинуть кластер будут посещены многоие из его вершин
Графы часто возникают при упрощении сложных систем. К примеру в виде графа удобно отображать:
- взамосвязи различных сайтов в интернете
- Социальные сети (сети контактов)
- Генные сети в молекулярной биологии
- порты, аэропорты, города (в качестве узлов графа)и пути их соединяюющие (в качестве ребер).
Следует отметить что случайное блуждание в графе - это конечная цепь Маркова.
В качестве метрики растояния можно использовать суммы длин ребер (или их количества) между двумя точками, что по сути является евклидовой метрикой.
общее описание метода
Метод опирается на следующе допущение -
расстояния между узлами графа относящихся к одному кластеру, меньше чем растояние между узлами относящимся к различным кластерам. т.е. поток внутри одного кластера много больше чем между кластерами.
т.е. если усиливать поток там где он силен и ослаблять его там где он слаб то согласно парадигме кластеризации графа границы между различными кластерами будут исчезать. Таким образом будет выявлена кластерная структура графа.
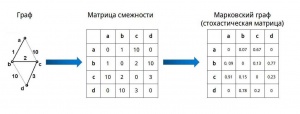
Моделирование потока в графе осуществляется путем преобразования его в марковский граф (см. рисуйнок 1).
На первом шаге граф преобразуется в матрицу растояний между узлами (иное представления графа). На втором шаге происходит преобразование матрицы растояний в матрицу стохастических переходов между узлами. В примере используется нормирование значений в столбце однако может быть применен любой другой алгоритм.
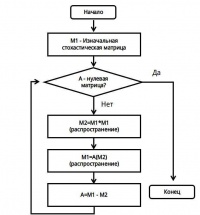
После того как стохастическая матрица (марковский граф) получена, к ней последовательно применяются применяются две функции (Expansion, распространение) и (Inflation, накачивание) до тех пор пока матррица не перестанет менятся (см. рисуйнок 2).
1) expansion - разширяем поток из вершины на потенциальных участников кластера.
2) inflation - уменьшаем переходы между кластерами и увеличиваем внутри кластера.
расширение (expansion) - объединяет кластера, остабляет сильный ток и усиливает слабый.
инфляция (inflation) - сжимает кластера, усиливает сильный поток и ослабляет слабый.
Марковский алгоритм кластеризации — быстрый и масштабируемый алгоритм кластеризации, основанный на моделировании потока в графе.
Примеры способов кластеризации
Расмотрим работу данного метода на примере кластеризации простого графа и его смежной матрицы.
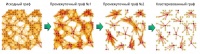
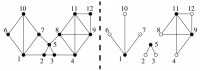
Возмем граф состоящий из 12 вершин и составим для него матрицу вероятностей переходов между узлами. Так как граф является не взвешенны вероятности перехода между соседними узлами и вероятность остаться в этом узле будет равна 1/(количество ребер смежных с вершиной + 1). Матрица представленна на рисунке 5. Таким образом мы получим матрицу. Процес MCL представлен на рисунке 5
итог по алгоритму
- Плюсы алгоритма
- Работает как с взвешенными, так и с невзвешенными графами
- Устойчив к шуму в данных
- Количество кластеров не указано заранее, но можно настроить степень детализации кластера
- Может находить кластера произвольной формы
- Минусы алгоритма
- Не нацелен находить перекрывающиеся кластеры (*)
- Не подходит для кластеров большого размера
- Часто кластеры получаются разного размера
- Время работы алгоритма в наихудшем случае Ο(V^3)
Дальнейшее развитие ,в 2012 году, метод получил как MLR-MCL R-MCL [Satuluri V. M. Scalable clustering of modern networks : дис. – The Ohio State University, 2012.]
В этих двух статьях двугой подход к кластеризации на графе:
L. Hagen and A. B. Kahng, A new approach to effective circuit clustering, in IEEE [91],
pp. 422–427.
C.-W. Yeh, C.-K. Cheng, and T.-T. Y. Lin, Circuit clustering using a stochastic flow injection
method, IEEE Transactions on Computer–Aided Design of Integrated Circuits and Systems,
14 (1995), pp. 154–162.
3.2.1 Приложения
- умножение разреженных матриц (распределения строк по разным процессора), параллельные вычисления, численное решение уравнений в частных производных .
Разреженное матричное умножение требует м. Минимизация объема связи между процессорами - это разбиение графа проблема. [A. Gupta, Fast and effective algorithms for graph partitioning and sparsematrix ordering, IBM Journal of Research & Development, 41 (1997). http://www.research.ibm.com/journal/rd/411/gupta.html]. Решатели PDE действуют на сетке или сетке, и параллельное вычисление такого решателя требует разделение сетки, опять же, чтобы минимизировать связь между процессами сорс [53]. планирование и размещение микросхем [C. J. Alpert and A. B. Kahng, Recent directions in netlist partitioning: a survey, Integration: the VLSI Journal, 19 (1995), pp. 1–81.] • Оценка требований к проводке и производительности системы в синтезаторе высокого уровня. Сис и поэтажное планирование.
- На сегодняшний день данный алгоритм применяется для данных в молекулярной биологии (выделение групп генов) [S. Brohee and J. van Helden. Evaluation of clustering algorithms for protein-
protein interaction networks. BMC Bioinformatics, 7, 2006.][J. Vlasblom and S.J. Wodak. Markov clustering versus affinity propagation for the partitioning of protein interaction graphs. BMC bioinformatics, 10(1):99, 2009.]
- анилизе изображений.
Список используемой литературы
1) Van Dongen, S. 2000. “Graph clustering by flow simulation.” Ph.D. thesis, University of Utrecht, The Netherlands
2) https://www.micans.org/mcl/index.html
3) Li, Li, Christian J. Stoeckert, and David S. Roos. "OrthoMCL: identification of ortholog groups for eukaryotic genomes." Genome research 13.9 (2003): 2178-2189.
4)Satuluri, Venu, Srinivasan Parthasarathy, and Duygu Ucar. "Markov clustering of protein interaction networks with improved balance and scalability." Proceedings of the first ACM international conference on bioinformatics and computational biology. ACM, 2010.