Порождение и выбор авторегрессионных моделей
Материал из MachineLearning.
| Строка 51: | Строка 51: | ||
По сглаженным данным строилась авторегрессионная матрица. При этом альтернaтивным вариантом к авторегрессионной модели являлась модель с восстановлением зависимости цены спота Y от векторов исходных погодных данных X и векторов f(X), где f - один из заранее заданных примитивов. | По сглаженным данным строилась авторегрессионная матрица. При этом альтернaтивным вариантом к авторегрессионной модели являлась модель с восстановлением зависимости цены спота Y от векторов исходных погодных данных X и векторов f(X), где f - один из заранее заданных примитивов. | ||
| - | Найденная авторегрессионная модель настраивалась [[LARS|методом наименьших углов | + | Найденная авторегрессионная модель настраивалась [[LARS|методом наименьших углов]]. Далее поточечно строился прогноз на следующий месяц. Так как прогноз строился последовательно, присутствует эффект накопления ошибки. |
=== Вычислительный эксперимент === | === Вычислительный эксперимент === | ||
Версия 22:03, 18 января 2010
Содержание |
Описание проекта
Цель
Целью исследования является прогноз среднесуточной цены на электроэнергию. Горизонт прогнозирования предполагается длиной в месяц.
Данные
В качестве исходных данных использовался временной ряд с 01.01.2003 по сегодняшний день. Во времеменных рядах были погода (различные интегральные индикаторы) и ежедневная цена на электричество. Нет данных по потреблению электричества и цене производства электроэнергии. Данные о закатах и рассветах брались из интернета.
Проверка качества
Временной ряд делился на исторические данные и последний месяц. Модель настраивается по истории и проверяется по этому месяцу. Процедура повторяется для каждого месяца последнего года. Критерий качества - MAPE (средняя абсолютная процентная ошибка).
Алгоритм настройки моделей
Метод наименьших углов (англ. least angle regression, LARS) - алгоритм отбора признаков в задачах линейной регрессии. Алгоритм предложили Бредли Эфрон, Тревор Хасти и Роберт Тибширани [1].
LARS решает следующую задачу. Пусть назначена линейная регрессионная модель. При большом количестве свободных переменных возникает проблема неустойчивого оценивания весов модели. LARS предлагает метод выбора такого набора свободных переменных, который имел бы наиболее значимую статистическую связь с зависимой переменной. Также LARS предлагает метод оценки весов.
Алгоритм LARS похож на алгоритм шаговой регрессии. Различие в том, что алгоритм LARS, вместо последовательного добавления свободных переменных, на каждом шаге изменяет их веса. Веса увеличиваются так, чтобы доставить наибольшую корреляцию с вектором регрессионных остатков. Основным достоинством LARS является то, что он выполняется за число шагов, не превышающее число свободных переменных. Частным случаем алгоритма LARS является алгоритм LASSO.
Постановка задачи
Задана выборка - матрица , столбцы которой соответствуют независимым переменным, а строки - элементам выборки и вектор
,
содержащий элементы зависимой переменной. Назначена линейная модель
.
Обозначим множество столбцов матрицы как
.
Пусть выполнены условия нормировки
Предполагается, что векторы линейно независимы.
Критерием качества модели назначена среднеквадратичная ошибка
Требуется найти для каждого шага LARS вектор весов и набор столбцов,
доставляющий наибольшую корреляцию векторов
и
.
Этапы решения
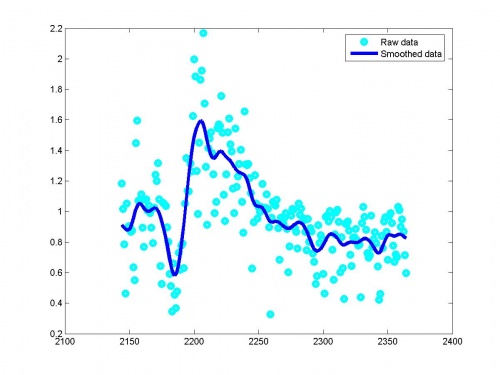
В начале работы алгоритма данные сглаживаются методом ядерного сглаживания. В качестве функции ядра была выбрана функция нормального распределения, а оптимальная ширина окна искалась по методу, предложенному Боумэном и Аззалини.
По сглаженным данным строилась авторегрессионная матрица. При этом альтернaтивным вариантом к авторегрессионной модели являлась модель с восстановлением зависимости цены спота Y от векторов исходных погодных данных X и векторов f(X), где f - один из заранее заданных примитивов.
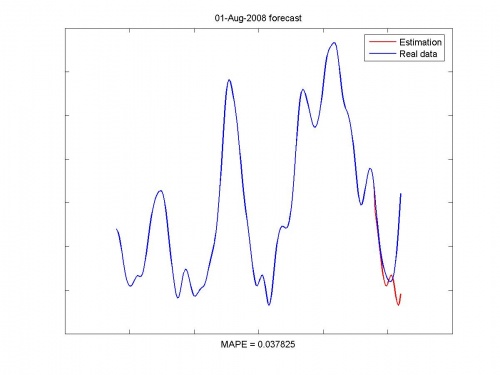
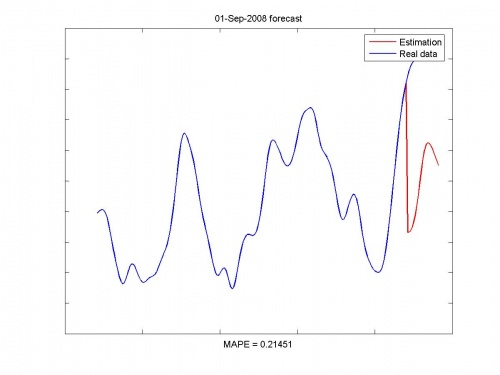
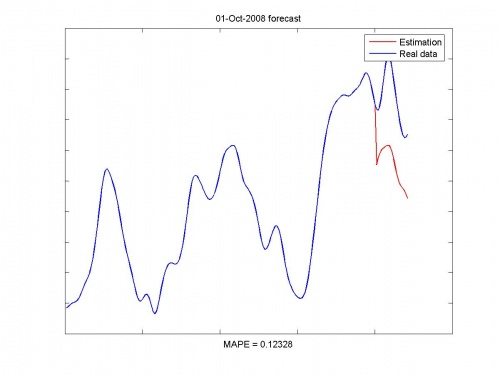
Найденная авторегрессионная модель настраивалась методом наименьших углов. Далее поточечно строился прогноз на следующий месяц. Так как прогноз строился последовательно, присутствует эффект накопления ошибки.
Вычислительный эксперимент
Программа состоит из нескольких модулей и основного исполняемого файла.
Код может быть предоставлен по запросу на irina.evgenjevna.lebedeva at gmail.com
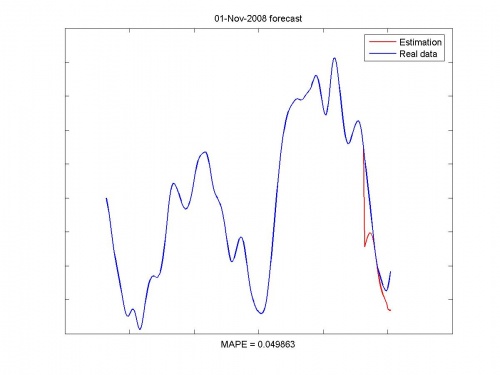
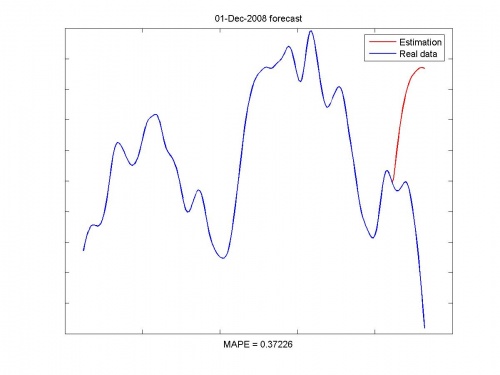
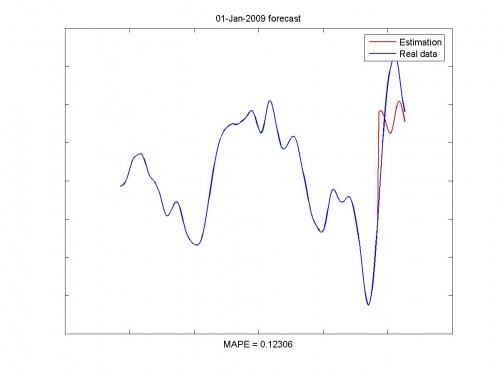
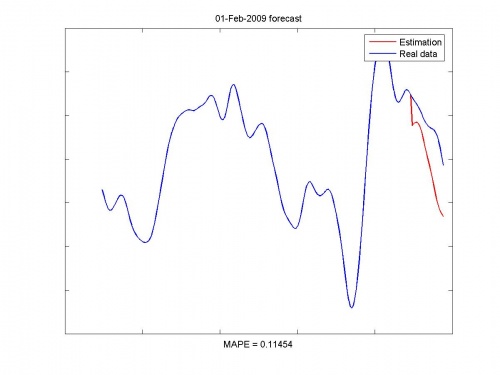
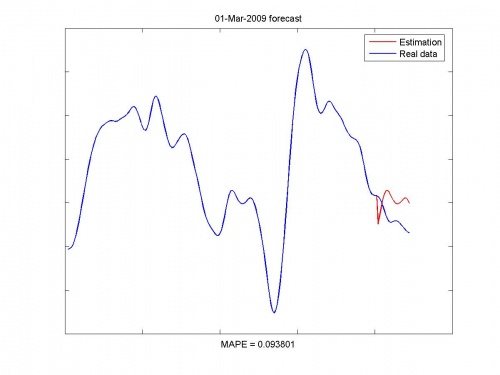
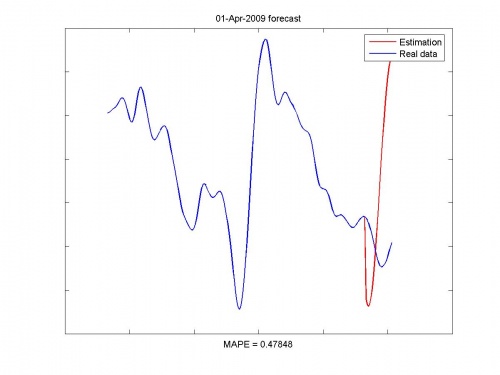
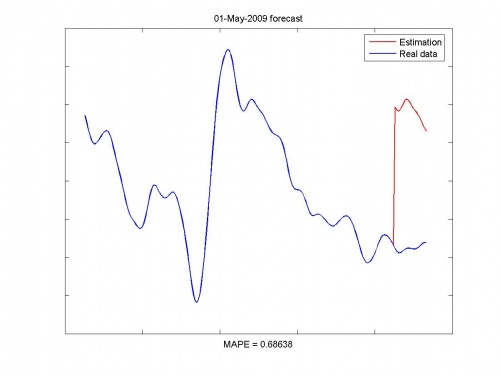
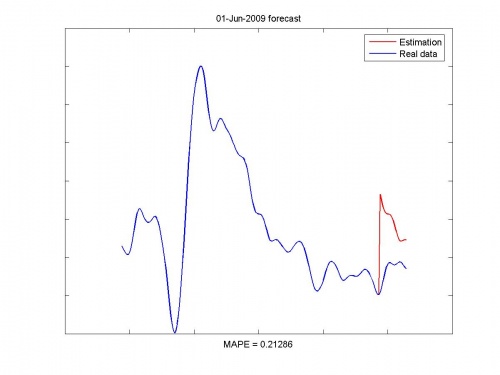
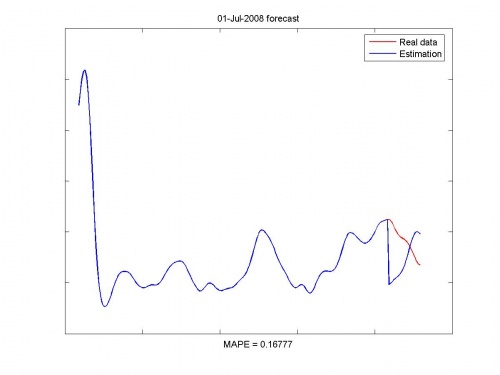
Иллюстрации работы программы:
Исходные данные и сглаживание:
Исходные данные и прогноз: