Фоновая поправка в анализе ДНК-микрочипов
Материал из MachineLearning.
м (→RMA-свёртка) |
м (→Ideal mismatch) |
||
| Строка 3: | Строка 3: | ||
Изначально для анализа фонового эффекта была разработана система так называемых PM-MM проб. Помимо нуклеотидных зондов, в точности соответствующих последовательности каждого рассматриваемого гена (Perfect Match probes), на микрочипах Affymetrix GeneChip размещались зонды, в которых средний (тринадцатый) олигонуклеотид был заменён на комплементарный (Mismatch probe). Предполагалось, что по интенсивности MM-проб можно будет оценить эффект неспецифической гибридизации и вычесть его из интенсивности PM-проб. Этот подход сразу же продемонстрировал свою несостоятельность - было показано, что в среднем для ДНК-микрочипа интенсивность около 30% MM-проб превышает интенсивность соответствующих им PM-проб<ref name="notMM">Naef F, Lim DA, Patil N, Magnasco MO. From features to expression: High-density oligonucleotide array analysis revisited. 2001. http://arxiv.org/abs/physics/0102010/.</ref>. Из-за этого вычитание интенсивностей MM-проб приводит к бессмысленному результату, поскольку экспрессия гена оказывается отрицательной. | Изначально для анализа фонового эффекта была разработана система так называемых PM-MM проб. Помимо нуклеотидных зондов, в точности соответствующих последовательности каждого рассматриваемого гена (Perfect Match probes), на микрочипах Affymetrix GeneChip размещались зонды, в которых средний (тринадцатый) олигонуклеотид был заменён на комплементарный (Mismatch probe). Предполагалось, что по интенсивности MM-проб можно будет оценить эффект неспецифической гибридизации и вычесть его из интенсивности PM-проб. Этот подход сразу же продемонстрировал свою несостоятельность - было показано, что в среднем для ДНК-микрочипа интенсивность около 30% MM-проб превышает интенсивность соответствующих им PM-проб<ref name="notMM">Naef F, Lim DA, Patil N, Magnasco MO. From features to expression: High-density oligonucleotide array analysis revisited. 2001. http://arxiv.org/abs/physics/0102010/.</ref>. Из-за этого вычитание интенсивностей MM-проб приводит к бессмысленному результату, поскольку экспрессия гена оказывается отрицательной. | ||
| - | Чтобы нейтрализовать этот эффект, компанией Affymetrix была разработана концепция Ideal Mismatch<ref name="affIM">Affymetrix. Statistical algorithms reference guide. Technical report, Affymetrix, Santa Clara, CA, 2001.</ref>. Идея заключается в том, чтобы делать обычную PM-MM коррекцию там, где это возможно, а в остальных случаях вычитать из интенсивности PM-проб некоторую величину, меньшую интенсивности MM-проб. Для каждого множества проб, соответствующих одному участку ДНК, вычисляется значение специфической фоновой интенсивности <tex>SB</tex>, представляющее собой устойчивое к выбросам среднее по каждой паре проб в множестве логарифмов отношений PM-интенсивностей к MM-интенсивностям. Если <tex>i</tex> - номер пробы, а <tex>k</tex> - номер подмножества проб, то фоновый эффект оценивается следующим выражением: | + | Чтобы нейтрализовать этот эффект, компанией Affymetrix была разработана концепция Ideal Mismatch<ref name="affIM">Affymetrix. Statistical algorithms reference guide. Technical report, Affymetrix, Santa Clara, CA, 2001. http://www.affymetrix.com/support/technical/technotes/statistical_reference_guide.pdf</ref>. Идея заключается в том, чтобы делать обычную PM-MM коррекцию там, где это возможно, а в остальных случаях вычитать из интенсивности PM-проб некоторую величину, меньшую интенсивности MM-проб. Для каждого множества проб, соответствующих одному участку ДНК, вычисляется значение специфической фоновой интенсивности <tex>SB</tex>, представляющее собой устойчивое к выбросам среднее по каждой паре проб в множестве логарифмов отношений PM-интенсивностей к MM-интенсивностям. Если <tex>i</tex> - номер пробы, а <tex>k</tex> - номер подмножества проб, то фоновый эффект оценивается следующим выражением: |
<tex>IM_i^{(k)} = \left\{MM_i^{(k)}, \:\:\: MM_i^{(k)}<PM_i^{(k)},\\ \frac{PM_i^{(k)}}{2^{SB_k}}, \:\:\: MM_i^{(k)}\geq PM_i^{(k)}, \: SB_k>\tau_c, \\ \frac{PM_i^{(k)}}{2^{\tau_c/(1+(\tau_c-SB_k)/\tau_s)}}, \:\:\: MM_i^{(k)}\geq PM_i^{(k)}, \: SB_k\leq\tau_c. \right.</tex> <br /> | <tex>IM_i^{(k)} = \left\{MM_i^{(k)}, \:\:\: MM_i^{(k)}<PM_i^{(k)},\\ \frac{PM_i^{(k)}}{2^{SB_k}}, \:\:\: MM_i^{(k)}\geq PM_i^{(k)}, \: SB_k>\tau_c, \\ \frac{PM_i^{(k)}}{2^{\tau_c/(1+(\tau_c-SB_k)/\tau_s)}}, \:\:\: MM_i^{(k)}\geq PM_i^{(k)}, \: SB_k\leq\tau_c. \right.</tex> <br /> | ||
| Строка 10: | Строка 10: | ||
Здесь <tex>\tau_c</tex> и <tex>\tau_s</tex> - настраиваемые параметры: <tex>\tau_c</tex> - константа различия со значением по умолчанию 0.03, <tex>\tau_s</tex> - константа масштабирования со значением по умолчанию 10. | Здесь <tex>\tau_c</tex> и <tex>\tau_s</tex> - настраиваемые параметры: <tex>\tau_c</tex> - константа различия со значением по умолчанию 0.03, <tex>\tau_s</tex> - константа масштабирования со значением по умолчанию 10. | ||
| - | Итоговое значение интенсивности для PM-проб с учётом фоновой поправки получается вычитанием из исходных значений интенсивностей PM-проб соответствующей им величины <tex>IM</tex>. | + | Итоговое значение интенсивности для PM-проб с учётом фоновой поправки получается вычитанием из исходных значений интенсивностей PM-проб соответствующей им величины <tex>IM</tex>. |
== RMA-свёртка == | == RMA-свёртка == | ||
Версия 07:34, 12 мая 2010
Фоновая поправка - важный предварительный этап в анализе ДНК-микрочипов. Его необходимость связана с наличием таких мешающих факторов, как шум оптической системы распознавания и неспецифическая гибридизация.
Содержание |
Ideal mismatch
Изначально для анализа фонового эффекта была разработана система так называемых PM-MM проб. Помимо нуклеотидных зондов, в точности соответствующих последовательности каждого рассматриваемого гена (Perfect Match probes), на микрочипах Affymetrix GeneChip размещались зонды, в которых средний (тринадцатый) олигонуклеотид был заменён на комплементарный (Mismatch probe). Предполагалось, что по интенсивности MM-проб можно будет оценить эффект неспецифической гибридизации и вычесть его из интенсивности PM-проб. Этот подход сразу же продемонстрировал свою несостоятельность - было показано, что в среднем для ДНК-микрочипа интенсивность около 30% MM-проб превышает интенсивность соответствующих им PM-проб[1]. Из-за этого вычитание интенсивностей MM-проб приводит к бессмысленному результату, поскольку экспрессия гена оказывается отрицательной.
Чтобы нейтрализовать этот эффект, компанией Affymetrix была разработана концепция Ideal Mismatch[1]. Идея заключается в том, чтобы делать обычную PM-MM коррекцию там, где это возможно, а в остальных случаях вычитать из интенсивности PM-проб некоторую величину, меньшую интенсивности MM-проб. Для каждого множества проб, соответствующих одному участку ДНК, вычисляется значение специфической фоновой интенсивности , представляющее собой устойчивое к выбросам среднее по каждой паре проб в множестве логарифмов отношений PM-интенсивностей к MM-интенсивностям. Если
- номер пробы, а
- номер подмножества проб, то фоновый эффект оценивается следующим выражением:
Здесь
RMA-свёртка
Данный метод фоновой коррекции является частью комплекса RMA методов для предобработки данных ДНК-микрочипов [1]. Используются только данные PM-проб. Значения интенсивности по ним корректируются отдельно по каждому микрочипу с использованием следующей модели распределения интенсивностей проб. Нескорректированное значение интенсивности представляется в виде суммы нормально распределённого шума
со средним
и дисперсией
и экспоненциально распределённого сигнала
со средним значением
. Чтобы исключить возможность получения отрицательных значений интенсивности, рассматривается только неотрицательная часть нормального распределения. Корректировка производится согласно следующей формуле:
где
,
и
- соответственно функция распределения и плотность стандартного нормального распределения.
MAS 5.0
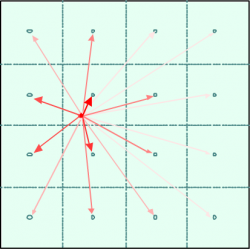
Данный метод делит каждый ДНК-микрочип на (по умолчанию 16) прямоугольных областей одинаковой площади, в каждой из которых фоновая поправка оценивается с помощью 2%-квантиля (наименьших значений) интенсивности
; оценивается также дисперсия наименьших 2% значений интенсивности
. Затем фоновая поправка для каждой пробы с координатами
рассчитывается как взвешенное среднее всех
оценок:
.
По аналогичной формуле с заменой на
рассчитывается дисперсия фоновой поправки для каждой пробы.
Веса зависят от расстояния между пробой и центрами прямоугольных областей:
где - евклидово расстояние между пробой и центром
-й ячейки,
- сглаживающий коэффициент (значение по умолчанию 100).
Скорректированное значение интенсивности рассчитывается по формуле где
- исходное значение интенсивности,
- параметр, соответствующий доле учитываемой вариации фоновой интенсивности (значение по умолчанию 0.5).