Машинное обучение и обучаемость: сравнительный обзор
Материал из MachineLearning.
(→МАШИННОЕ ОБУЧЕНИЕ И ОБУЧАЕМОСТЬ: СРАВНИТЕЛЬНЫЙ ОБЗО�) |
(категория, ссылки, оформление) |
||
| (5 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
В статье проведен сравнительный анализ различных определений обучаемости, рассмотрены необходимые и достаточные условия обучаемости, | В статье проведен сравнительный анализ различных определений обучаемости, рассмотрены необходимые и достаточные условия обучаемости, | ||
| - | указаны границы применимости VC теории. Дополнительно выявленные фундаментальные положения дают объяснение практически наблюдаемой обучаемости при использовании некоторых алгоритмов и моделей обучения, несмотря на кажущееся противоречие с VC теорией: в действительности этого противоречия нет. | + | указаны границы применимости [[Теория Вапника-Червоненкиса|VC теории]]. Дополнительно выявленные фундаментальные положения дают объяснение практически наблюдаемой обучаемости при использовании некоторых алгоритмов и моделей обучения, несмотря на кажущееся противоречие с VC теорией: в действительности этого противоречия нет. |
| - | Ниже представлена таблица, в которую сведены основные используемые в теории машинного обучения определения обучаемости и их характеристики. За таблицей следуют выводы, касающиеся условий обучаемости и значения VC размерности. | + | Ниже представлена таблица, в которую сведены основные используемые в теории [[Машинное обучение|машинного обучения]] определения обучаемости и их характеристики. За таблицей следуют выводы, касающиеся условий обучаемости и значения [[Размерность Вапника-Червоненкиса|VC размерности]]. |
| - | [[Изображение: | + | |
| - | + | [[Изображение:Lernability.jpeg]] | |
| - | В теории В. Н. Вапника в определении равномерной сходимости фигурирует только семейство H, из которого извлекается гипотеза. Универсальное эмпирическое обобщение не оговаривает явно ни семейство G, в котором содержится неизвестный концепт, ни семейство H. Тем не менее, при любом подходе к машинному обучению его результатом является выбранная обучающим алгоритмом A гипотеза h, принадлежность которой некоторому семейству H предопределена выбором для решения задачи нейронных сетей, решающих деревьев, SVM или других моделей. Если это семейство H оказывается очень широким (вплоть до того, что его VC размерность не ограничена), обучаемость все же может иметь место, если образ ImA обучающего алгоритма (алгоритмического отображения) A во множестве H достаточно узок. | + | |
| + | В теории [[Вапник, Владимир Наумович|В. Н. Вапника]] в определении равномерной сходимости фигурирует только семейство H, из которого извлекается гипотеза. Универсальное эмпирическое обобщение не оговаривает явно ни семейство G, в котором содержится неизвестный концепт, ни семейство H. Тем не менее, при любом подходе к машинному обучению его результатом является выбранная обучающим алгоритмом A гипотеза h, принадлежность которой некоторому семейству H предопределена выбором для решения задачи нейронных сетей, решающих деревьев, SVM или других моделей. Если это семейство H оказывается очень широким (вплоть до того, что его VC размерность не ограничена), обучаемость все же может иметь место, если образ ImA обучающего алгоритма (алгоритмического отображения) A во множестве H достаточно узок. | ||
Для разных обучающих выборок гипотеза, выбираемая обучающим алгоритмом A, вообще говоря, может оказаться различной. Вводя своеобразную окрестность каждой обучающей выборки как множество выборок, получающихся из исходной путем удаления (Loo) или замены (RO) ровно одного примера, можно определить понятие устойчивости, оценивая степень изменения выбираемой алгоритмом A гипотезы. Не удивительно, что устойчивые алгоритмы обучения порождают достаточно "узкие" образы в семействе H. | Для разных обучающих выборок гипотеза, выбираемая обучающим алгоритмом A, вообще говоря, может оказаться различной. Вводя своеобразную окрестность каждой обучающей выборки как множество выборок, получающихся из исходной путем удаления (Loo) или замены (RO) ровно одного примера, можно определить понятие устойчивости, оценивая степень изменения выбираемой алгоритмом A гипотезы. Не удивительно, что устойчивые алгоритмы обучения порождают достаточно "узкие" образы в семействе H. | ||
| Строка 26: | Строка 21: | ||
Дополнительно выявленные фундаментальные положения дают объяснение практически наблюдаемой обучаемости при использовании некоторых алгоритмов и моделей обучения, несмотря на кажущееся противоречие с VC теорией: в действительности этого противоречия нет. | Дополнительно выявленные фундаментальные положения дают объяснение практически наблюдаемой обучаемости при использовании некоторых алгоритмов и моделей обучения, несмотря на кажущееся противоречие с VC теорией: в действительности этого противоречия нет. | ||
| + | |||
| + | == Источники == | ||
| + | * В. И. Донской [http://intellectualarchive.com/getfile.php?file=6kEaOEViwnV&orig_file=Donskoy%20Mach%20Learning%20Survey.pdf] | ||
| + | |||
| + | [[Категория:Популярные и обзорные статьи]] | ||
Текущая версия
В статье проведен сравнительный анализ различных определений обучаемости, рассмотрены необходимые и достаточные условия обучаемости, указаны границы применимости VC теории. Дополнительно выявленные фундаментальные положения дают объяснение практически наблюдаемой обучаемости при использовании некоторых алгоритмов и моделей обучения, несмотря на кажущееся противоречие с VC теорией: в действительности этого противоречия нет.
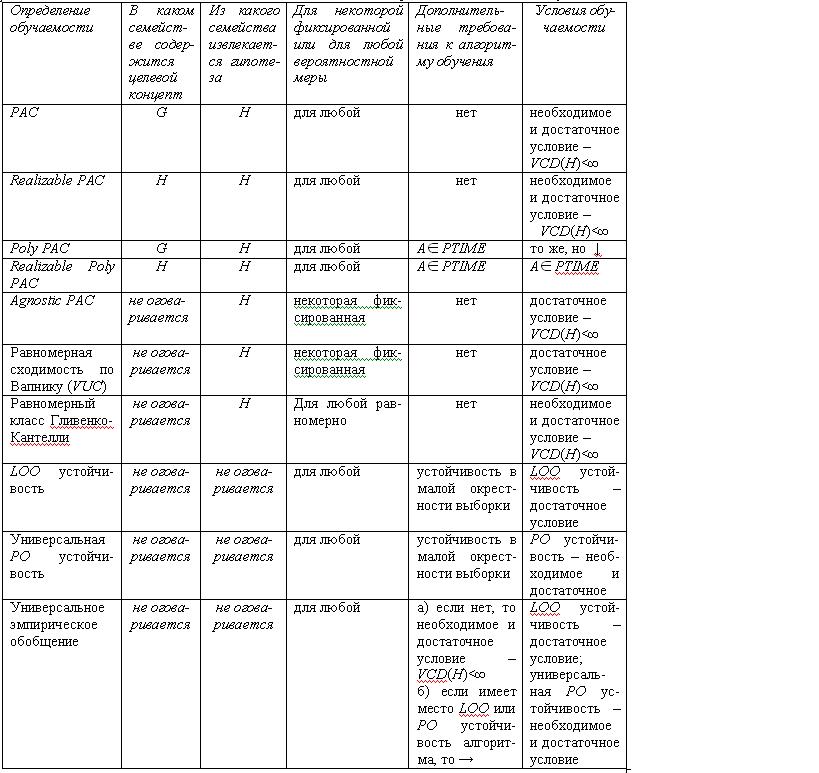
Ниже представлена таблица, в которую сведены основные используемые в теории машинного обучения определения обучаемости и их характеристики. За таблицей следуют выводы, касающиеся условий обучаемости и значения VC размерности.
В теории В. Н. Вапника в определении равномерной сходимости фигурирует только семейство H, из которого извлекается гипотеза. Универсальное эмпирическое обобщение не оговаривает явно ни семейство G, в котором содержится неизвестный концепт, ни семейство H. Тем не менее, при любом подходе к машинному обучению его результатом является выбранная обучающим алгоритмом A гипотеза h, принадлежность которой некоторому семейству H предопределена выбором для решения задачи нейронных сетей, решающих деревьев, SVM или других моделей. Если это семейство H оказывается очень широким (вплоть до того, что его VC размерность не ограничена), обучаемость все же может иметь место, если образ ImA обучающего алгоритма (алгоритмического отображения) A во множестве H достаточно узок.
Для разных обучающих выборок гипотеза, выбираемая обучающим алгоритмом A, вообще говоря, может оказаться различной. Вводя своеобразную окрестность каждой обучающей выборки как множество выборок, получающихся из исходной путем удаления (Loo) или замены (RO) ровно одного примера, можно определить понятие устойчивости, оценивая степень изменения выбираемой алгоритмом A гипотезы. Не удивительно, что устойчивые алгоритмы обучения порождают достаточно "узкие" образы в семействе H.
Считается, что фундаментальным результатом статистической теории обучения является следующий строго доказанный факт.
Если H – класс концептов (решающих правил) над проблемной областью с произвольной вероятностной мерой и выполняются все необходимее условия измеримости, то следующие три утверждения эквивалентны:
- Для класса H имеет место PAC обучаемость для любой вероятностной меры.
- H является равномерным классом Гливенко-Кантелли.
- VCD(H) является конечной.
Подходы к определению обучаемости и устойчивости и полученные на их основе результаты позволяют расширить представление о статистической теории обучения. Теория равномерной сходимости, PAC обучаемость и универсальная способность к обобщению представляют собой достаточно широко определенные модели. В них не оговариваются ни свойства распределения вероятностей, ни особенности алгоритма обучения, которые полагаются произвольными.Фиксация свойств алгоритма обучения (в частности, его заведомая устойчивость) позволяют сузить модель обучения и вследствие этого получить обучаемость даже в случае бесконечной VC размерности семейства гипотез, в которое вложен образ алгоритма обучения A. Конечность VC размерности также перестает быть необходимым условием в некоторых случаях при конкретизации вероятностной меры (например, в случае диффузных или атомарных мер).
Дополнительно выявленные фундаментальные положения дают объяснение практически наблюдаемой обучаемости при использовании некоторых алгоритмов и моделей обучения, несмотря на кажущееся противоречие с VC теорией: в действительности этого противоречия нет.
Источники
- В. И. Донской [1]