Графические модели (курс лекций)/2012/Задание 4
Материал из MachineLearning.
(Новая: {{stop| '''Задание находится в разработке.'''<br/> Не приступайте к выполнению задания до его официальной выд...) |
(выдача) |
||
| (2 промежуточные версии не показаны) | |||
| Строка 1: | Строка 1: | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
{{TOCright|300px}} | {{TOCright|300px}} | ||
| Строка 17: | Строка 12: | ||
Доказать, что каждый возможный разрез этой конструкции соответствует определенной разметке переменных. | Доказать, что каждый возможный разрез этой конструкции соответствует определенной разметке переменных. | ||
| + | |||
| + | Привести пример прикладной задачи, где такая энергия может возникнуть. К каким эффектам приведет ее использование? | ||
Подсказка: <tex> -x_1\dots x_n = \min_z \left( (n-1)z - zx_1 - \dots - zx_n \right) </tex>. | Подсказка: <tex> -x_1\dots x_n = \min_z \left( (n-1)z - zx_1 - \dots - zx_n \right) </tex>. | ||
| Строка 28: | Строка 25: | ||
Доказать, что каждый возможный разрез этой конструкции соответствует определенной разметке переменных. | Доказать, что каждый возможный разрез этой конструкции соответствует определенной разметке переменных. | ||
| + | |||
| + | Привести пример прикладной задачи, где такая энергия может возникнуть. К каким эффектам приведет ее использование? | ||
=== Задача 3 === | === Задача 3 === | ||
| Строка 35: | Строка 34: | ||
=== Задача 4 === | === Задача 4 === | ||
| - | Рассмотрим двойственное разложение энергии <tex> E(x) = |x_1 - x_2| | + | Рассмотрим двойственное разложение энергии <tex> E(x) = -|x_1 - x_2| - |x_2 - x_3| - |x_3 - x_1|</tex> на две компоненты: |
| - | <tex> |x_1 - x_2| | + | <tex> -|x_1 - x_2| - |x_2 - x_3| </tex> и <tex> -|x_3 - x_1|</tex>. |
Здесь все переменные бинарны. | Здесь все переменные бинарны. | ||
| + | |||
Построить график двойственной функции. Есть ли зазор между прямой и двойственной задачами? Ответ обосновать. | Построить график двойственной функции. Есть ли зазор между прямой и двойственной задачами? Ответ обосновать. | ||
| + | |||
| + | Что изменится (не изменится), если изменить способ разложения энергии на компоненты? | ||
=== Задача 5 === | === Задача 5 === | ||
| - | Рассмотрим двойственное разложение энергии <tex> E(x) = |x_1 - x_2| | + | Рассмотрим двойственное разложение энергии <tex> E(x) = -|x_1 - x_2| - |x_2 - x_3| - |x_3 - x_4| - |x_4 - x_1|</tex> на две компоненты: |
| - | <tex> |x_1 - x_2| | + | <tex> -|x_1 - x_2| - |x_2 - x_3| - |x_3 - x_4| </tex> и <tex> -|x_4 - x_1|</tex>. |
| + | Здесь все переменные бинарны. | ||
| + | |||
| + | Построить график двойственной функции. Есть ли зазор между прямой и двойственной задачами? Ответ обосновать. | ||
| + | Что изменится (не изменится), если изменить способ разложения энергии на компоненты? | ||
=== Оформление задания === | === Оформление задания === | ||
Текущая версия
|
Начало выполнения задания: 9 апреля 2012
Срок сдачи: 18 апреля 2012, 18.00
Задача 1
Построить граф, минимальный разрез которого соответствует минимизации энергии .
Здесь
— бинарные переменные,
— скобка Айверсона.
Доказать, что каждый возможный разрез этой конструкции соответствует определенной разметке переменных.
Привести пример прикладной задачи, где такая энергия может возникнуть. К каким эффектам приведет ее использование?
Подсказка: .
Задача 2
Построить граф, минимальный разрез которого соответствует минимизации энергии .
Здесь
.
Здесь
— бинарные переменные,
— скобка Айверсона.
Доказать, что каждый возможный разрез этой конструкции соответствует определенной разметке переменных.
Привести пример прикладной задачи, где такая энергия может возникнуть. К каким эффектам приведет ее использование?
Задача 3
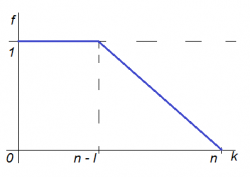
Как при помощи комбинации конструкций из задачи 2 построить конструкцию для минимизации энергии , где f — произвольная вогнутая, кусочно-линейная функция?
Задача 4
Рассмотрим двойственное разложение энергии на две компоненты:
и
.
Здесь все переменные бинарны.
Построить график двойственной функции. Есть ли зазор между прямой и двойственной задачами? Ответ обосновать.
Что изменится (не изменится), если изменить способ разложения энергии на компоненты?
Задача 5
Рассмотрим двойственное разложение энергии на две компоненты:
и
.
Здесь все переменные бинарны.
Построить график двойственной функции. Есть ли зазор между прямой и двойственной задачами? Ответ обосновать.
Что изменится (не изменится), если изменить способ разложения энергии на компоненты?
Оформление задания
Выполненный вариант задания необходимо сдать лектору в бумажном виде или прислать на bayesml@gmail.com в электронном виде. Для решения задания можно использовать собственноручно написанные программные средства. Если таковые используются, то их тоже необходимо прислать.