Обсуждение:Практикум на ЭВМ (317)/2011-2012
Материал из MachineLearning.
(→Метод ближайшего соседа) |
м («Обсуждение:Практикум на ЭВМ (317)» переименована в «Обсуждение:Практикум на ЭВМ (317)/2011-2012»: Страница устарела) |
||
| (114 промежуточных версий не показаны.) | |||
| Строка 352: | Строка 352: | ||
Шкалу, наверное, стоит разметить, так ничего не понятно из графика. [[Участник:Ildar|Ildar]] 08:44, 11 марта 2012 (MSK) | Шкалу, наверное, стоит разметить, так ничего не понятно из графика. [[Участник:Ildar|Ildar]] 08:44, 11 марта 2012 (MSK) | ||
| + | |||
| + | Если я поставлю отметки, то я выложу наилучшие параметры работы knn, и не принесу команде никакой пользы (медвежья услуга). Я показала, что при полном переборе соседей и порога возможно достичь такого результата. Тем более в моем алгоритме может быть ошибка. | ||
| + | [[Участник:Ekaterina|Ekaterina]] 22:02, 11 марта 2012 (MSK) | ||
=== Нормировка исходных данных и линейные классификаторы === | === Нормировка исходных данных и линейные классификаторы === | ||
| Строка 386: | Строка 389: | ||
[[Участник:MoRandi91|Andrew Ostapets]] 20:50, 19 февраля 2012 (MSK) | [[Участник:MoRandi91|Andrew Ostapets]] 20:50, 19 февраля 2012 (MSK) | ||
| + | |||
| + | == Анализ тематик текста == | ||
| + | |||
| + | Цель этого раздела — эксперименты с вероятностными моделями тематик в текстах. Задача вероятностной модели — описать, как из '''скрытых данных''' (в данном случае это информация о наличии тематики в документе, в каких пропорциях документ содержит тематики) получаются '''наблюдаемые данные''' (в данном случае: наличие терминов [слов] в документе, частота термина или его "сила", "вес"). Алгоритмы, которые работают с тематическими моделями, настраивают модель так, чтобы наблюдаемые данные выглядели правдоподобно в рамках модели, а из настроенной модели извлекается нужная информация. | ||
| + | |||
| + | Батя тематических моделей — весьма веселый мужик [http://www.cs.princeton.edu/~blei/index.html Prof. David M. Blei]. У него есть страница [http://www.cs.princeton.edu/~blei/topicmodeling.html подборкой материалов] с по тематическому моделированию. В т.ч. [http://www.cs.princeton.edu/~blei/papers/Blei2011.pdf general introduction] с описанием идей методов, текст не требует дополнительных знаний о байесовском моделировании, но после него (в принципе) можно успешно использовать весь софт. Еще есть методичка Кропотова с курса БММО: [http://www.machinelearning.ru/wiki/images/8/82/BMMO11_14.pdf], но она для понимания скорее всего потребует чтения [http://www.machinelearning.ru/wiki/images/5/57/BMMO11_9.pdf] и [http://www.machinelearning.ru/wiki/images/6/6b/BMMO11_10.pdf]. | ||
| + | |||
| + | === Модель LDA === | ||
| + | |||
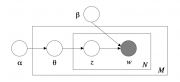
| + | [[Изображение:LDA_bayesnet.png|thumb|Графическое представление модели (байесовская сеть), изображены зависимости между переменными]] | ||
| + | |||
| + | LDA (Latent Dirichlet Allocation) — модель смеси тематик, в которой слова формируются следующим образом. | ||
| + | |||
| + | Пусть есть D документов, T тематик, для документа d известно, что он содержит N<sub>d</sub> слов. Для каждого документа d: | ||
| + | # Выбирается вектор θ<sub>d</sub> ~ Dir(α), θ<sub>d</sub> = (θ<sub>d,1</sub>, ..., θ<sub>d,T</sub>) из [http://en.wikipedia.org/wiki/Dirichlet_distribution распределения Дирихле], что дает ∑<sub>t</sub>θ<sub>d,t</sub>=1. Переменная '''θ<sub>d,t</sub>''' означает пропорцию, с которой тематика t входит в документ d. | ||
| + | # Для всех слов в документе n = 1..N<sub>d</sub>: | ||
| + | :* Выбирается тематика слова '''z<sub>d,n</sub>''', случайно из дискретного распределения с вектором вероятностей θ<sub>d</sub>. | ||
| + | :* Выбирается само слово (термин), '''w<sub>d,n</sub>''' из дискретного распределения, заданного вектором вероятностей '''β<sub>t</sub>''', где t = z<sub>d,n</sub> (выбранная тематика). | ||
| + | Основным параметром в этой модели являются вектора вероятностей '''β<sub>t</sub>''', t=1..T. Число β<sub>t,w</sub> — вероятность того что термином, относящимся к тематике t оказался термин t. Этот параметр (β) собственно и оптимизируется. Еще, как правило, оптимизируется параметр распределения Дирихле (α), еще на вектора β можно навесить априорное распределение Дирихле и их параметры тоже оптимизировать, но это уже детали. | ||
| + | |||
| + | === Использование софта с сайта [http://www.cs.princeton.edu/~blei/topicmodeling.html] === | ||
| + | |||
| + | На радость крестьянину, все эти прожки следуют более-менее одному формату представления данных. Формат прост и описан в [http://www.cs.princeton.edu/~blei/lda-c/readme.txt readme.txt], а вот скриптик, который переводит матрицу <tt>X</tt> (из data.mat) в файл с входными данными для [http://www.cs.princeton.edu/~blei/lda-c/index.html lda-c]. | ||
| + | |||
| + | Обученная модель состоит из файлов: | ||
| + | * ???.beta: матрица T × W из значений log β<sub>t,w</sub>. | ||
| + | * ???.other: остальные параметры (число тематик, параметр α, ...) | ||
| + | |||
| + | Файлы со значениями скрытых переменных (z, θ): | ||
| + | * ???.gamma: матрица D × T из значений log q(θ<sub>d</sub>) — логарифма распределения Дирихле (вернее его неточной оценки), которое является апостериорной оценкой параметра θ<sub>d</sub> | ||
| + | * word-assignment.dat: буквально значения z, т.е. соответствия слов тематикам, наверное эта информация достаточно бесполезна. | ||
| + | |||
| + | === LDA, вариационный EM-алгоритм === | ||
| + | |||
| + | Статья: [http://www.cs.princeton.edu/~blei/papers/BleiNgJordan2003.pdf]. | ||
| + | Реализация: [http://www.cs.princeton.edu/~blei/lda-c/index.html]. | ||
| + | |||
| + | Обученные модели: | ||
| + | * LDA var-EM, 100 topics, raw data, train+test (20K documents) [http://dl.dropbox.com/u/20300574/jrs12_topic/lda100.zip lda100.zip] <small>обучалась порядка 10 часов</small> | ||
| + | * LDA var-EM, 200 topics, raw data, train+test (20K documents) [http://dl.dropbox.com/u/20300574/jrs12_topic/lda200.zip lda200.zip] <small>обучалась почти ровно сутки :)</small> | ||
| + | |||
| + | '''Замечание:''' помимо подхода с вариационным приближением есть подход к обучению LDA методом монте-карло по схеме Гиббса. Какой из подходов лучше зависит от задачи, вряд ли это сможет принципиально улучшить качество категоризации, но есть спортивный интерес. | ||
| + | |||
| + | === Модификация LDA для выделения тематик, соответствующих категориям из задачи === | ||
| + | |||
| + | '''Цель''': Сделать так, чтобы в ходе настройки тематики выделялись не «с потолка», а именно те, которые соответствуют категориям. Для этого у нас есть информация по каждому документу в виде списка категорий, к которым он относится. | ||
| + | |||
| + | '''Модификация''': В исходной модели, пропорции тематик (θ<sub>1</sub>, ..., θ<sub>T</sub>) генерируются случайно из распределения Dir(θ<sub>1</sub>, ..., θ<sub>T</sub> | α). Давайте будем считать, что нам известно, какие тематики в документе присутствуют: t<sub>1</sub>, ..., t<sub>s</sub>. Модифицируем исходную модель: будем брать пропорции тематик (θ<sub>t<sub>1</sub></sub>, ..., θ<sub>t<sub>s</sub></sub>) из распределения Dir(θ<sub>t<sub>1</sub></sub>, ..., θ<sub>t<sub>s</sub></sub> | α), а остальные пропорции положим θ<sub>j</sub> = 0 (иных тематик в документе совсем нет). | ||
| + | |||
| + | Более формально: положим известной величину <tex>\mathcal{Y} = (y_{d,t})</tex>, y<sub>d,t</sub> = [тематика t содержится в документе d]. Полное правдоподобие модели: | ||
| + | <tex>p(\mathcal{W}, \mathcal{Z}, \Theta | \Phi, \alpha, \mathcal{Y}) = \prod_{d=1}^D p(\theta_d|\alpha,y_d) \prod_{n=1}^{N_d} p(w_{d,n}|z_{d,n}, \Phi) p(z_{d,n}|\theta_d, y_d)</tex>. | ||
| + | |||
| + | Для настройки модели будем максимизировать неполное правдоподобие с условием известной информации о категориях: <tex>p(\mathcal{W}|\Phi,\alpha,\mathcal{Y}) \to \max_{\Phi, \alpha}</tex>. | ||
| + | |||
| + | Все формулы для вариационного EM-алгоритма выводятся без принципиальных изменений: | ||
| + | :<tex>q(\Theta, \mathcal{Z}|\gamma_d,\mu_d) \approx p(\Theta, \mathcal{Z} | \mathcal{W}, \Phi, \alpha, \mathcal{Y})</tex> | ||
| + | :<tex>q(\theta_d|\gamma_d) = \text{Dir}(\theta_{d,{t_1}}, \dots, \theta_{d,{t_s}}|\gamma_{t_1}, \dots, \gamma_{t_s}) \cdot [\theta_{d,t'_1}=0, \dots, \theta_{d,t'_{s'}}=0]</tex> | ||
| + | ::<tex>\gamma_{t_j} = \alpha + \sum_{n=1}^{N_d}\mu_{d,n,t_j}</tex>, на <tex>\gamma_{t'_j}</tex> пофиг — они не нужны | ||
| + | :<tex>q(z_{d,n}|\mu_{d,n}) = \mu_{d,n,z_{d,n}}</tex> | ||
| + | ::<tex>\mu_{d,n,t} = y_{d,t} \cdot \frac{\Phi_{t, w_{d,n}} \exp(\Psi(\gamma_{d,t}))}{\sum_{k=t_1}^{t_s} \Phi_{k,w_{d,n}} \exp(\Psi(\gamma_{d,k}))}</tex> | ||
| + | :<tex>\Phi^{\text{new}}_{t,w} = \frac{\sum_{(d,n): w_{d,n}=w} \mu_{d,n,t}}{\sum_{d,n} \mu_{d,n,t}}, \quad \alpha^{\text{new}}</tex> — без изменений. | ||
| + | : Здесь t<sub>1</sub>, ..., t<sub>s</sub> обозначены тематики, содержащиеся в данном документе, тогда как t'<sub>1</sub>, ..., t'<sub>s'</sub> — не содержащиеся. | ||
| + | |||
| + | '''Реализация''': код [http://www.cs.princeton.edu/~blei/lda-c/index.html lda-c] написан достаточно неплохо, думаю его можно легко модифицировать под новую модель. | ||
| + | |||
| + | '''Использование новой модели''': | ||
| + | * Самое банальное: поставить каждой категории в соответствие тематику, обучать модель с 83 тематиками. Гораздо понятнее, как перевести апостриорные вероятности этих тематик в ответ к нашей задаче. | ||
| + | * Выделение смесей тематик в каждой категории: каждой категории поставить в соответствие K тематик, таким образом модель будет содержать 83·K тематик, после обучения мы будем иметь для каждой категории K апостериорных вероятностей. | ||
| + | |||
| + | === Использование моделей для категоризации === | ||
| + | |||
| + | Да, да... Это самый полезный вопрос. Давайте подумаем над ним вместе. | ||
| + | |||
| + | [[Участник:Peter Romov|Peter Romov]] 23:25, 14 марта 2012 (MSK) | ||
| + | |||
| + | |||
| + | ===Сэмплирование Гиббса и его модификация для задачи классификации=== | ||
| + | |||
| + | Одна из быстрых реализаций метода LDA - это сэмплирование Гиббса. Алгоритм можно посмотреть на слайде(справа). | ||
| + | [[Изображение:Algorithm.jpg|thumb]] | ||
| + | |||
| + | Будем рассматривать обучение и контроль как единую коллекцию документов. Коллекция частично размечена - мы знаем принадлежности обучающих документов к темам. Такую постановку можно трактовать как задачу с частичным обучением - semi-supervised learning. Все что нужно изменить в GS - это учесть известную информацию в начальных приближениях. Я делала это так: | ||
| + | |||
| + | Длины документов n<sub>d</sub> - просто суммируем матрицу данных по строкам. | ||
| + | |||
| + | Число слов в документе посвященное теме n<sub>td</sub> (для обучения) - | ||
| + | 0, если документ не отнесен к этой теме; | ||
| + | длина документа делить на число тем, к которым он отнесен по классификации, если отнесен. | ||
| + | |||
| + | Число слов w, относящихся к теме n<sub>wt</sub> (подсчитанное по обучению) - | ||
| + | каждое слово каждого документа распределяем в равных долях по темам, к которым отнесен документ. | ||
| + | |||
| + | Число слов в документе посвященное теме n<sub>td</sub> (для контроля) - | ||
| + | считаем, что каждое слово документа принадлежит теме t в доле n<sub>wt</sub> / n<sub>w</sub>, где n<sub>w</sub> - сколько всего таких слов в обучении. | ||
| + | |||
| + | Число слов w, относящихся к теме n<sub>wt</sub> (досчитанное по контролю) - | ||
| + | Каждое слово на контроле добавляет к n<sub>wt</sub> величину n<sub>wt</sub> / n<sub>w</sub>, заметим, что распределение слова по темам при этом не меняется. | ||
| + | |||
| + | Число слов в теме n<sub>t</sub> - просто суммируем матрицу n<sub>wt</sub> по столбцам. | ||
| + | |||
| + | Далее реализуем описанный на слайде алгоритм. Замечу, что в данном случае длина документа очень велика, поэтому внутренний цикл я вела не по всем словам документа, а по его различным словам, а значит, выбирала единую тему на все вхождений конкретного слова в документ. Это не очень хорошо, потому что обновление счетчиков, связанное с распределением большого числа вхождений одного и того же слова может заметно сказаться на распределении p(t|d) - сместить его. Чтобы этого избежать, стоит разбить внутренний цикл по различным словам на два таких цикла. В первом пересчитывать распределение p(t|w,d), в другом выбирать тему и обновлять счетчики. | ||
| + | |||
| + | Итак, получился алгоритм классификации. Результаты осмысленные, но не очень хорошие - 0.40. Однако это я считала учитывая только первые 4000 признаков из 10000 (ненулевые менее чем на 10 документах отброшены) и всего лишь с 10 сэмплами. Считалось несколько часов. Запустила на 100 сэмплов и по всем признаком - за сутки не посчитала. Надо 1) толково отобрать признаки - princomp, ppca пока упорно отвечают мне out of memory, 2) запустить с бОльшими, но подъемными цифрами и посмотреть, улучшится ли качество. | ||
| + | |||
| + | [[Участник:AnyaP|AnyaP]] 01:57, 19 марта 2012 (MSK) | ||
| + | |||
| + | == Структурный SVM == | ||
| + | |||
| + | Не могу больше... выложу PDF. | ||
| + | |||
| + | [[Участник:Peter Romov|Peter Romov]] 03:07, 15 марта 2012 (MSK) | ||
== Идеи == | == Идеи == | ||
* '''Цепочка независимых классификаторов.''' Как использовать простую классификацию на два класса, но все таки учитывать зависимости между метками принадлежности тематикам? Например так: принимать решение по тематике 1 исключительно по признакам, решение по тематике 2 принимать по {признакам + принадлежности тематике 1}, …, решение по тематике N принимать по {признакам + решениям о тематиках 1…N-1}. То есть образовать «цепочку» из классификаторов. [[Участник:Peter Romov|Peter Romov]] 21:41, 9 февраля 2012 (MSK) | * '''Цепочка независимых классификаторов.''' Как использовать простую классификацию на два класса, но все таки учитывать зависимости между метками принадлежности тематикам? Например так: принимать решение по тематике 1 исключительно по признакам, решение по тематике 2 принимать по {признакам + принадлежности тематике 1}, …, решение по тематике N принимать по {признакам + решениям о тематиках 1…N-1}. То есть образовать «цепочку» из классификаторов. [[Участник:Peter Romov|Peter Romov]] 21:41, 9 февраля 2012 (MSK) | ||
| + | : Вот, кстати: [http://www.icis.ntu.edu.sg/scs-ijit/119/119_2.pdf Liwei et. al., Parallel and Sequential Support Vector Machines for Multi-label Classification]. Примерно то, что я имел в виду — простая идея объединения бинарных SVM-ов. [[Участник:Peter Romov|Peter Romov]] 03:27, 15 марта 2012 (MSK) | ||
* '''Разбиения.''' Зафиксировать несколько разбиений имеющейся обучающей выборки на тренировочную/тестовую, которую все будут использовать для оценки точности алгоритма. Это может быть полезно так как: 1) он-лайн система тестирования считает качество алгоритма на случайном подмножестве всей тестовой выборки (в правилах написано, что используется ≈10 % объектов), то есть оценка качества может быть неточной; 2) количество попыток отправить ответ на тестовой выборке ограничено 200 попытками, это много, но все же. [[Участник:Peter Romov|Peter Romov]] 21:48, 9 февраля 2012 (MSK) | * '''Разбиения.''' Зафиксировать несколько разбиений имеющейся обучающей выборки на тренировочную/тестовую, которую все будут использовать для оценки точности алгоритма. Это может быть полезно так как: 1) он-лайн система тестирования считает качество алгоритма на случайном подмножестве всей тестовой выборки (в правилах написано, что используется ≈10 % объектов), то есть оценка качества может быть неточной; 2) количество попыток отправить ответ на тестовой выборке ограничено 200 попытками, это много, но все же. [[Участник:Peter Romov|Peter Romov]] 21:48, 9 февраля 2012 (MSK) | ||
| Строка 697: | Строка 812: | ||
[[Участник:Kuraga|Kuraga]] 14:36, 29 февраля 2012 (MSK) | [[Участник:Kuraga|Kuraga]] 14:36, 29 февраля 2012 (MSK) | ||
| + | |||
| + | == Отчеты == | ||
| + | |||
| + | Публикуем здесь наши отчеты. | ||
| + | |||
| + | === Куракин Александр === | ||
| + | [http://www.machinelearning.ru/wiki/index.php?title=%D0%98%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5:Report.pdf Отчет] | ||
| + | |||
| + | [http://www.machinelearning.ru/wiki/index.php?title=%D0%98%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5:Kurakin_prac_12_03.zip Код] | ||
| + | |||
| + | Сам я вряд ли чем-то помог группе, кроме того, что немного описал о Shogun'е, и то, о нем мне Петр рассказал. Хотя с его помощью можно было просто реализовать многие вещи — каждый мог этим воспользоваться. | ||
| + | |||
| + | Мне помогли: Петр Ромов, Евгений Нижибицкий, Андрей Остапец, Дмитрий Кондрашкин, Аня Потапенко, Максим Новиков. | ||
| + | |||
| + | === Малышева Екатерина === | ||
| + | [http://www.machinelearning.ru/wiki/index.php?title=%D0%98%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5:Report_mek.pdf Отчет] | ||
| + | |||
| + | === Потапенко Анна === | ||
| + | [http://www.machinelearning.ru/wiki/index.php?title=%D0%98%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5:Report-Potapenko.pdf Отчет] | ||
| + | |||
| + | === Любимцева Мария === | ||
| + | [http://www.machinelearning.ru/wiki/index.php?title=%D0%98%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5:Report_mlyub.pdf Отчет] | ||
| + | |||
| + | === Фонарев Александр === | ||
| + | [http://www.machinelearning.ru/wiki/index.php?title=%D0%98%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5:Fonarev_full_report.pdf Отчет] | ||
| + | |||
| + | === Исмагилов Тимур === | ||
| + | [http://www.machinelearning.ru/wiki/index.php?title=%D0%98%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5:Ismagilov_report5.pdf Отчет] | ||
| + | |||
| + | === Огнева Дарья === | ||
| + | [[Media:Mmp_Practice2012_Ogneva_report.pdf|Отчет]] | ||
| + | |||
| + | === Нижибицкий Евгений === | ||
| + | [http://www.machinelearning.ru/wiki/index.php?title=%D0%98%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5:Jrs2012_nizhibitsky.pdf Отчет] | ||
| + | |||
| + | [http://www.machinelearning.ru/wiki/index.php?title=%D0%98%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5:JRS2012.zip Код] | ||
| + | |||
| + | === Кондрашкин Дмитрий === | ||
| + | [[Media:Report_rus.pdf|Отчет]] | ||
| + | |||
| + | === Остапец Андрей === | ||
| + | [[Media:Andrew_Ostapets.pdf|Отчет]] | ||
| + | |||
| + | === Китаец Зак Евгений === | ||
| + | [http://www.machinelearning.ru/wiki/index.php?title=%D0%98%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5:Zakzak.pdf Отчет] | ||
| + | |||
| + | === Лобачева Екатерина === | ||
| + | [[Media:Biopapers.pdf|Отчет]] | ||
| + | |||
| + | === Дьяконов Александр === | ||
| + | [http://alexanderdyakonov.narod.ru/DyakonovReportBIOMED.pdf отчёт] | ||
| + | |||
| + | === Гавриков Михаил === | ||
| + | [http://www.machinelearning.ru/wiki/index.php?title=%D0%98%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5:%D0%9E%D1%82%D1%87%D1%91%D1%82_%D0%93%D0%B0%D0%B2%D1%80%D0%B8%D0%BA%D0%BE%D0%B2_%D0%9C%D0%B8%D1%85%D0%B0%D0%B8%D0%BB_%D0%BF%D0%BE_%D0%BF%D1%80%D0%B0%D0%BA%D1%82%D0%B8%D0%BA%D1%83%D0%BC%D1%83.pdf] | ||
| + | [http://www.machinelearning.ru/wiki/images/1/19/Gavrot4et.pdf] | ||
| + | |||
| + | === Шаймарданов Ильдар === | ||
| + | [[Media:Shaimardanov-Report.pdf|Отчет]] | ||
| + | |||
| + | === Березин Алексей === | ||
| + | [http://ompldr.org/vZGI5Zw отчёт] [[Участник:BerAl|Berezin]] 16:04, 9 апреля 2012 (MSD) | ||
| + | |||
| + | === Новиков Максим === | ||
| + | [http://www.creativeobject.ru/prak/Report_novikov.pdf отчёт] | ||
| + | [[Участник:Novikov|Novikov]] 17:04, 9 апреля 2012 (MSD) | ||
| + | |||
| + | === Морозова Дарья === | ||
| + | [http://www.machinelearning.ru/wiki/images/f/fa/Report_morozova.pdf] | ||
| + | [[Участник:Morozova|Morozova]] 18:38, 9 апреля 2012 (MSD) | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | = Пакет R = | ||
| + | ==Распределение по пакетам== | ||
| + | {|class = "standard sortable" | ||
| + | ! class="unsortable"|№ п/п !! Студент !! Пакет | ||
| + | |- | ||
| + | | align="center"|2 || Березин Алексей Андреевич || align="center"|[http://cran.gis-lab.info/web/packages/LogicForest/index.html LogicForest] | ||
| + | |- | ||
| + | | align="center"|3 || [[Участник:Borman|Борисов Михаил Викторович]] || align="center"|[http://cran.r-project.org/web/packages/tm/index.html tm] | ||
| + | |- | ||
| + | | align="center"|4 || Гавриков Михаил Игоревич ||align="center"|[http://cran.gis-lab.info/web/packages/mathgraph/index.html mathgraph] | ||
| + | |- | ||
| + | | align="center"|5 || Зак Евгений Михайлович || align="center"|[http://cran.gis-lab.info/web/packages/RWeka/index.html RWeka] | ||
| + | |- | ||
| + | | align="center"|6 || Исмагилов Тимур Ниязович || align="center"|[http://cran.gis-lab.info/web/packages/Boruta/index.html Boruta] | ||
| + | |- | ||
| + | | align="center"|7 || Кондрашкин Дмитрий Андреевич || align="center"|[] | ||
| + | |- | ||
| + | | align="center"|8 || [[Участник:Kuraga|Куракин Александр Владимирович]] || align="center"|[http://cran.gis-lab.info/web/packages/lasso2/index.html lasso2] | ||
| + | |- | ||
| + | | align="center"|9 || Лобачева Екатерина Максимовна || align="center"|[http://cran.gis-lab.info/web/packages/ROCR/index.html ROCR] | ||
| + | |- | ||
| + | | align="center"|10 || Любимцева Мария Михайловна || align="center"|[http://cran.gis-lab.info/web/packages/nnet/index.html nnet] | ||
| + | |- | ||
| + | | align="center"|11 || Малышева Екатерина Константиновна || align="center"|[http://cran.gis-lab.info/web/packages/LiblineaR/index.html liblinearR] | ||
| + | |- | ||
| + | | align="center"|12 || Морозова Дарья Юрьевна ||align="center"|[http://cran.gis-lab.info/web/packages/rminer/index.html rminer] | ||
| + | |- | ||
| + | | align="center"|13 || [[Участник:Nizhibitsky|Нижибицкий Евгений Алексеевич]] || align="center"|[] | ||
| + | |- | ||
| + | | align="center"|14 || [[Участник:Novikov|Новиков Максим Сергеевич]] || align="center"|[http://cran.gis-lab.info/web/packages/randomForest/index.html randomForest] | ||
| + | |- | ||
| + | | align="center"|15 || Огнева Дарья Сергеевна || align="center"|[http://cran.gis-lab.info/web/packages/arules/index.html arules] | ||
| + | |- | ||
| + | | align="center"|16 || [[Участник:MoRandi91|Остапец Андрей Александрович]] || align="center"|[] | ||
| + | |- | ||
| + | | align="center"|17 || Потапенко Анна Александровна || align="center"|[] | ||
| + | |- | ||
| + | | align="center"|18 || [[Участник:Peter Romov|Ромов Петр Алексеевич]] || align="center"|[http://cran.r-project.org/web/packages/bnlearn/index.html bnlearn], [http://www.shogun-toolbox.org/doc/en/current/r_modular_examples.html shogun_modular] | ||
| + | |- | ||
| + | | align="center"|19 || [[Участник:Newo|Фонарев Александр Юрьевич]] || align="center"|[http://cran.gis-lab.info/web/packages/gbm/index.html gbm] | ||
| + | |- | ||
| + | | align="center"|20 || Шаймарданов Ильдар Рифарович || align="center"|[http://cran.r-project.org/web/packages/lda/index.html LDA] | ||
| + | |- | ||
| + | |} | ||
| + | </noinclude> | ||
| + | |||
| + | ==Отчеты== | ||
| + | |||
| + | ===Малышева Екатерина=== | ||
| + | [http://www.machinelearning.ru/wiki/images/d/d5/Report_LiblineaR.pdf Отчет по liblinearR] | ||
| + | |||
| + | ===Куракин Александр=== | ||
| + | [http://www.machinelearning.ru/wiki/index.php?title=%D0%98%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5:Report-kurakin-2012-04-r.pdf Отчет по lasso2] | ||
| + | |||
| + | [[Участник:Kuraga|Kuraga]] 21:15, 20 апреля 2012 (MSD) | ||
| + | |||
| + | ===Борисов Михаил=== | ||
| + | [http://ompldr.org/vZGhiNA/borisov_r_tm.pdf Отчёт по tm] | ||
| + | |||
| + | ===Гавриков Михаил=== | ||
| + | [http://www.machinelearning.ru/wiki/images/c/cd/Review_mathgraph_by_gavr.pdf Отчёт по mathgraph] | ||
| + | |||
| + | ===Любимцева Мария=== | ||
| + | [http://www.machinelearning.ru/wiki/images/8/81/Nnet_report.pdf Отчет по nnet] | ||
| + | |||
| + | ===Новиков Максим=== | ||
| + | [http://www.creativeobject.ru/prak/Report_Novikov_R_randomForest.pdf Отчёт по randomForest] | ||
| + | |||
| + | ===Фонарев Александр=== | ||
| + | [http://www.machinelearning.ru/wiki/images/a/a7/Fonarev_r_gbm.pdf Отчет по gbm] | ||
| + | |||
| + | ===Шаймарданов Ильдар=== | ||
| + | [http://www.machinelearning.ru/wiki/images/5/58/Report_Ildar.pdf Отчет по LDA] | ||
| + | |||
| + | ===Березин Алексей=== | ||
| + | [http://beralez.narod2.ru/BerezinR.pdf Отчет по LogicForest] | ||
| + | |||
| + | ===Лобачева Екатерина=== | ||
| + | [[Media:ROCR.pdf|Отчет по ROCR]] | ||
| + | |||
| + | ===Исмагилов Тимур=== | ||
| + | [http://www.machinelearning.ru/wiki/images/3/37/Report7ismagilov.pdf Отчет по Boruta] | ||
| + | |||
| + | ===Ромов Петр=== | ||
| + | [[Media:Practice_Romov_R_bnlearn.pdf|Отчет по bnlearn]] | ||
| + | |||
| + | ===Огнева Дарья=== | ||
| + | [[Media:ArulesReport.pdf|Отчет по arules]] | ||
| + | |||
| + | ===Председатель Фан-Клуба Зак Евгений=== | ||
| + | [http://www.machinelearning.ru/wiki/index.php?title=%D0%98%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5:ReportRweka.pdf Отчет по RWeka] | ||
| + | |||
| + | ===Морозова Дарья=== | ||
| + | [http://www.machinelearning.ru/wiki/images/8/86/Morozova_rminer.pdf Отчет по Rminer] | ||
Текущая версия
Реальная задача «Topical Classification of Biomedical Research Papers»
| | Итак, результат 0.482 можно получить простой MATLAB-программой (всего 940 байт с комментариями!), используя лишь стандартные функции size, sparse, bsxfun, full и т.д. На стареньком ноутбуке все вычисления (кроме загрузки данных) занимают 1 минуту. Дь-ов 16:32, 13 февраля 2012 (MSK) |
Постановка, данные
Подробное описание задачи: [1].
Объект (журнальная статья) описывается 25640 признаками --- целые числа 0...1000. Каждый признак означает насколько сильно журнальная статья связана с медецинским термином. Признаковые описания разреженные: большая часть признаков у одного объекта равны 0, что означает что одна журнальная статья связана лишь с небольшим числом медецинских терминов.
Имеется 83 тематик (topics). По признаковому описанию журнальной статьи нужно сказать, к каким тематикам она относится. Выход классификатора: подмножество чисел 1..83.
Данные:
- тренировочная выборка, 10'000 объектов, для каждого объекта список тематик, к которым он относится
- тестовая выборка, 10'000 объектов
На сайте соревнования выложены текстовые файлы с матрицами объект-признак, после распаковки они весят под 500МБ и очень долго считываются в матлаб. Я сделал MAT-файл data.mat (ссылка в рассылке), в котором лежат sparse-матрицы (вид представления матриц в матлабе при котором запоминается список ненулевых элементов матрицы):
-
X,X_t— объект-признак для тренировочной и тестовой выборок; -
Y— матрица правильных ответов для тренировочной выборки, размера 10'000x83, в каждой строке стоят единицы на месте столбцов с номерами выбраных тематик.
Матлаб функция, которая записывает результат классификации, представленный в виде матрицы Nx83 (как Y), в файл готовый для отправки в систему: [2].
Пример: решение, которое каждому объекту ставит в соответствие 5 наиболее часто встречаемых тематик
load('data.mat'); [~, idx] = sort(sum(Y), 'descend'); % после чего в idx номера тематик в порядке убывания их популярности Y_t = sparse(size(X_t, 1), size(Y, 2)); % пустая матрица ответа Y_t(:,idx(1:5)) = 1; % для каждого объекта выбираем 5 наиболее популярных тематик sparse2labels(Y_t, 'majority.csv');
Peter Romov 16:15, 9 февраля 2012 (MSK)
Замечание: Целых 1723 признака имеют только нулевые значения на всех объектах обучающей выборки. Смело их выкидываем! Уменьшим немного матрицу данных и обезопасим себя от inf при нормировках. AnyaP 0:59, 26 февраля 2012 (MSK)
И сделать это можно так:
X_t = X_t(:,any(X)); X = X(:,any(X));
nizhibitsky 00:22, 26 февраля 2012 (MSK)
Система оценки
Качество результата подсчитывается при помощи стандартной в Information Retrieval метрике: F-score.
Введем обозначения:
- N — число документов
- TrueTopicsi — множество верно предсказаных тематик для i-го документа
- PredTopicsi — множество предсказанных тематик для i-го документа
Величины Precision и Recall для документа i:
Можно самому подсчитывать качество работы алгоритма на некоторой проверочной выборке, при условии что к ней есть правильные ответы (ground truth).
Обратите внимание: результат, которые выдает система он-лайн проверки подсчитывается на случайном подмножестве тестовой выборки, в 10 раз меньшем всей тестовой выборки.
Peter Romov 22:16, 9 февраля 2012 (MSK)
Пример matlab кода для вычисление F-меры:
function F=fscore(Y,A) %Y-predicted %A-true %Y and A are n x 83 matrices where n is the size of validation set %Y(i,j)==1 if i document refers to j topic N=size(Y,1); Y=(Y==1)'; A=(A==1)'; c=(Y==1)&(A==1); tp=sum(c); p=tp./sum(Y==1); r=tp./sum(A==1); f=2*(p.*r)./(p+r); F=sum(f(~isnan(f)))/N;
Kondra 23:13, 12 февраля 2012 (MSK)
Тестирование
Тестировать лучше на своей машине. Для этого можно разбивать множество объектов на два случайных подмножества: обучение и контроль. А затем проводить серию обучение/тестирование на нескольких случайных разбиениях.
matlab код функции разбивающей данные на два случайных подмножества:
function [X,Y,Xt,Yt]=splitData(S,y,n) %S-матрица объект-признак %y-матрица ответов %n-желаемый размер первого множества [m,~]=size(S); idx=randperm(m); X=S(idx(1:n),:); Y=y(idx(1:n),:); Xt=S(idx((n+1):end),:); Yt=y(idx((n+1):end),:);
Тестировать можно так:
function [favg,f]=test(S,y,n,m) %S-матрица объект-признак %y-матрица ответов %n-количество серий %m-желаемый размер контрольного множества %favg-усредненная f-мера по серии тестов %f-массив f-мер f=zeros(n,1); for i=1:n [X,Y,Xt,Yt]=splitData(S,y,m); model=train(Xt,Yt); label=classify(X,model); f(i)=fscore(label,Y); end favg=sum(f)/n;
Разница между оценкой, полученной данным способом, и оценкой с сайта не превосходила .
Kondra 23:43, 12 февраля 2012 (MSK)
- Я думаю стоит зафиксировать разбиения и выложить его сюда, чтобы мы могли честно сравнивать результат. Peter Romov 09:24, 13 февраля 2012 (MSK)
Вывод результата
Код программы создания файла, готового к отправке на сайт
function MakeSubmit(Y_p,filename) %Y_p - ответы классификатора %filename - имя для файла с ответами fid=fopen(filename,'w'); for i=1:size(Y_p,1) I=find(Y_p(i,:)); if size(I,2)>0 fprintf(fid,'%d',I(1)); else fprintf(fid,'44'); %44 - самая встречаемая рубрика end fprintf(fid,',%d',I(2:end)); fprintf(fid,char(10)); end fclose(fid);
Ildar 21:20, 14 февраля 2012 (MSK)
Замечание: Необходимо строчку добавления меток через запятую обрамить if-ом, иначе будет получаться файл, не принимаемый системой
if length(I) > 1 fprintf(fid,',%d',I(2:end)); end
Maria Lyubimtseva 21:02, 10 марта 2012 (MSK)
Преобразование файла ответов в матрицу из 0 и 1
Код преобразует txt файл с ответами для обучающей выборки в матрицу размера: "кол-во объектов в обучающей выборке" на 83. Если объект j принадлежит к i-му классу, то в A(j, i) стоит 1, иначе 0. Уверена, что можно реализовать намного проще, но пока что то не придумала ничего лучше.
Y = csvread('trainingLabels.txt'); [a, ~] = size(Y(:,1)); A = zeros(a, 83); for i = 1 : a A(i, Y(i, Y(i, :) ~= 0)) = 1; end
Ekaterina 19:50, 28 февраля 2012 (MSK)
Эксперименты
Независимые классификаторы
Идея: свести задачу предсказания "подмножества" к задаче классификации на 2 класса.
Обучаем набор из 83 классификаторов для независимого решения по каждой тематике, каждый классификатор соответствует одной тематике и отвечает на вопрос "относится/не относится".
На некоторых объектах может получиться так, что ни один классификатор не дал положительного результата, но результат "пустое множество тематик" не допускается по правилам.
- Эту проблему я решил эвристически: такие объекты привязываются к одной тематике, выбирается та тематика, чей классификатор дал наиболее близкое к положительному решающее значение, т.е. чей классификатор наименее уверенно ответил отрицательно на вопрос "относится ли объект к тематике?" Таких объектов в тестовой выборке оказалось 188 (линейные классификаторы). Peter Romov 21:28, 9 февраля 2012 (MSK)
Утверждение: признаков в 2.5 раз больше числа объектов ⇒ по отношению к одной тематике, обучающая выборка линейно разделима, очень уверенно разделима. Peter Romov 21:28, 9 февраля 2012 (MSK)
| Классификатор | Результат (он-лайн) | Примечание |
|---|---|---|
| Линейные L2-reg L2-loss L1-reg L2-loss L2-reg L1-loss liblinear | 0.393 | Различные постановки задачи обучения дали одинаковые ответы (с точностью до выбора тематик), подбор коэффициента регуляризации бессмысленен (уверенная линейная разделимость). Что можно сделать: регулировать пороги решающих правил. |
Предположение: другие классификаторы / методы, принимающие решения независимо, будут давать схожий результат; предположение независимости принадлежности статьи к разным тематикам очень наивно и нужно двигаться в сторону учета зависимостей между тематиками. Peter Romov 21:28, 9 февраля 2012 (MSK)
Замечание: после нормировки данных, произошло улучшение(результат 0.437). До этого было 0.4 и на некоторых признаках свм не сходился, теперь на любом признаке сходится за 10-15 итераций. Kondra 23:24, 15 февраля 2012 (MSK)
- Не ясно, что значит свм не сходился. За сколько итераций сходимость не была достигнута? Каким методом оптимизировался функционал? Какое значение С? (как правило, чем выше С, тем больше нужно итераций) Peter Romov 01:27, 20 февраля 2012 (MSK)
Замечание: Если использовать нормировку по максимуму, то можно добиться результата 0.471. Andrew Ostapets 23:14, 18 февраля 2012 (MSK)
Замечание: Если использовать нормировку по максимуму, то можно добиться результата 0.509. nizhibitsky 16:39, 19 февраля 2012 (MSK)
Вывод: Если использовать линейные классификаторы, принимающие решения независимо, то можно получить достаточно высокий результат.
Идея: Попробовать различные преобразования признаков, и уже на них запускать линейные классификаторы. Andrew Ostapets 9:31, 19 февраля 2012 (MSK)
Идея: Для каждого класса подбирать свой оптимальный линейный классификатор. nizhibitsky 20:57, 19 февраля 2012 (MSK)
Классификация данных как текста (метрический алгоритм)
Идея: Считаем, что представленные величины являются просто количеством соответствующих терминов в тексте, так же используем независимые классификаторы по всем рубрикам.
Заменяем матрицу данных на классическую матрицу из весов :
-
(term frequency — частота слова) — отношение числа вхождения некоторого слова к общему количеству слов документа. Таким образом, оценивается важность термина в пределах отдельного документа:
-
(inverse document frequency — обратная частота документа) — инверсия частоты, с которой некоторый термин встречается в документах коллекции. Учитывает тот факт, что если термин встречается во многих документах множества, то он не может являться существенным критерием принадлежности документа рубрике и наоборот:
После нормализации полученных весов строим т.н. «центроиды» — стандартизированные представители рубрик — просто среднее арифметическое векторов-представителей данной рубрики и запускаем простой метрический алгоритм для тестовой выборки — относим вектора к центроидам, которые ближе, чем некий порог, либо к минимально близкому из практических соображений.
Более подробно можно посмотреть, например, в дипломной работе.
Результат: Удалось достичь результата 0.306 с упущенной из виду нормировкой весов — итоговую функцию можно посмотреть здесь. (Вектора относятся к классам, центроиды которых удалены не более, чем на 0.8. Время построения матрицы весов — 25 минут, время классификации тестовой выборки — 2.5 часа на C2Dm/2.5GHz).
Пути улучшения: Попробовать другие метрики, модификации матрицы .
nizhibitsky 21:32, 12 февраля 2012 (MSK)
Можно попробовать использовать косинусную меру. Kondra 19:41, 15 февраля 2012 (MSK)
Результат: Получено качество 0.39. Используется описанная матрица весов TF-IDF, метрика евклидова, объекты относятся к 5 наиболее близким центроидам.
Сравнение метрик: Попробуем использовать различные метрики для подсчета расстояний от классифицируемых объектов до центроидов. Полученные результаты:
- 1. Евклидова метрика - 0.39
- 2. Манхэттенское расстояние - 0.17
- 3. Косинусная мера - 0.38
- 4. Расстояние Чебышева - 0.18
Идея: Евклидова метрика и косинусная мера дают неплохое качество классификации. Логично их каким-то образом совместить. На практике разные совмещения не дали существенного улучшения: результат 4.00, условие отнесения документа к рубрике "одна из 5 ближайших по евклидовой мере И близость по косинусной мере больше порога(0.024)". Возможно, причина в схожести совмещаемых алгоритмов.
Подумать на будущее:
- 1. Я отношу документ к 5 наиболее близким центроидам(рубрикам). Если аккуратно подобрать пороговое значение, то с условием "расстояние меньше порогового" результаты подобные, но не лучше. Как ещё можно преобразовать матрицу расстояний до центроидов в матрицу итоговой классификации?
- 2. Хочется учесть различную "скученность" рубрик: насколько близко к своим центроидам расположены представители. Пробовала использовать среднее расстояние от представителей до центроида, максимальное, медиану, расстояние от к-ого соседа центроида - качество классификации только портится.
AnyaP 01:51, 26 февраля 2012 (MSK)
Смысл матрицы данных
Матрица данных не похожа на матрицу встречаемости терминов в документах :(
1. Около 10 тысяч «слов» встречаются не более чем в 10 документах из 10 000. Интуитивно кажется, что таких редких слов должно быть меньше. В любом случае, логично удалить эти слова-признаки. (Оценка, полученная в метрическом классификаторе с весами TF-IDF при таком удалении не изменилась).
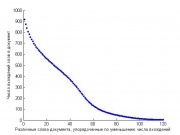
2. Максимальная длина документа около 60 000 слов, средняя – 30 000, минимальная 20 000. При этом максимальное число различных слов в документе – 200, среднее – 100, минимальное 60. Получается, в документе одни и те же слова повторяются очень много раз. На графике справа показано, сколько раз встречается в документе каждое его слово. (Мы взяли 500 документов средней длины, упорядочили в каждом из них слова по уменьшению числа вхождений и усреднили число вхождений каждого i-го по популярности слова по выбранным документам (в разных документах это разные слова))
3. Можно было бы предположить, что у нас куча стоп-слов, и они и повторяются по много раз в каждом документе. Но нет – стоп-слова, употребительные слова языка должны встречаться в бОльшей части коллекции – а слов, которые встречаются более чем в 1000 документах из 10 000 – нет.
После таких наблюдений кажется неразумным применять к задаче методы анализа текстовых коллекций topic modeling (pLSA, LDA), а хотелось.
AnyaP 18:27, 8 марта 2012 (MSK)
Эксперименты с метрическим алгоритмом
Получен результат 0.369. Описание: tf*idf, нормализация. В качестве ответа берется ближайший сосед по косинусной мере. Улучшения: оптимизировать число соседей. Kondra 23:57, 15 февраля 2012 (MSK)
Подбор числа соседей(пока что несколько вариантов вручную) привел к результату 0.462. Планирую сделать автоматический перебор. Ответ считается где-то за 16 секунд.(Core i7 3.40GHz) Kondra 23:40, 16 февраля 2012 (MSK)
Сделал автоподбор k, существенного улучшения от 0.46 нету. Попробую некоторые вариации tf*idf и нормировок. Kondra 20:55, 17 февраля 2012 (MSK)
Идея: попробовать SVD. Kondra 13:54, 18 февраля 2012 (MSK)
Выделение частичной иерархии
Идея: Наилучшим продолжением идеи Евгения Зака о поиске «часто вместе встречающихся» рубрик будет вычисление поддержки — ничто иное как условная вероятность совместной встречи категорий.
Реализация: Составляем матрицу условных вероятностей, например, так:
sup = zeros(83,83); for i=1:83 for j=1:83 if sum(y(:,j)>0.5)~=0 && i~=j sup(i,j) = sum(y(:,i)>0.5&y(:,j)>0.5)/sum(y(:,j)>0.5); end end end
Здесь - вероятность наличия рубрики
при наличии рубрики
(я не уверен в каноничности порядка индексов — гугл не признается, как же правильно записывается support).
Промежуточные результаты: Например, можно посмотреть максимально вероятную рубрику-пару для данной, и упорядочить по этой максимальной вероятности:
| если есть | то есть | с вероятностью |
|---|---|---|
| 46 | 50 | 71% |
| 52 | 73 | 69% |
| 73 | 52 | 65% |
| 50 | 46 | 65% |
| 40 | 42 | 53% |
Вывод. Скорее всего, рубрика 50 является «хирургией» для «переломов» 46 (не наоборот!).
nizhibitsky 13:04, 13 февраля 2012 (MSK)
Метод ближайшего соседа
Функция, считающая расстояние в метрике Евклида. На входе: матрица X, размерность D*N, D - размерность вектора, N - количество векторов. Матрица Y, размерность D*P, D - размерность вектора, P - количество векторов.
На выходе: матрица D размера N*P, где в D(n,p) представлен квадрат евклидового расстояния между X(:,n) и Y(:,p).
function d = cvEucdist(X, Y) if ~exist('Y', 'var') || isempty(Y) %% Y = zeros(size(X, 1), 1); U = ones(size(X, 1), 1); d = abs(X'.^2*U).'; return; end V = ~isnan(X); X(~V) = 0; % V = ones(D, N); U = ~isnan(Y); Y(~U) = 0; % U = ones(D, P); d = abs(X'.^2*U - 2*X'*Y + V'*Y.^2);
Ekaterina 22:50, 15 февраля 2012 (MSK)
- Екатерина, код — это ok. Но здесь наиболее важно писать результат эксперимента, хотя бы он-лайн, или можно на кросс-валидации. Peter Romov 23:44, 15 февраля 2012 (MSK)
Постановка эксперимента:
Выборка 3 раза разбивалась на 2 не пересекающихся подмножества в соотношении 9:1. На 9 частях производилось обучение, на 1 части производился контроль. Затем для каждого набора параметров производилось усреднение на 3-х экспериментах. На графике по оси Y сверху вниз отложено количество рассматриваемых соседей. По оси X - порог, то есть в скольких соседях встречается этот класс. Цвет - качество классификации, шкала приведена рядом с изображением.
Ekaterina 14:21, 9 марта 2012 (MSK)
Шкалу, наверное, стоит разметить, так ничего не понятно из графика. Ildar 08:44, 11 марта 2012 (MSK)
Если я поставлю отметки, то я выложу наилучшие параметры работы knn, и не принесу команде никакой пользы (медвежья услуга). Я показала, что при полном переборе соседей и порога возможно достичь такого результата. Тем более в моем алгоритме может быть ошибка. Ekaterina 22:02, 11 марта 2012 (MSK)
Нормировка исходных данных и линейные классификаторы
Как уже писалось ранее, в этой задачи независимые линейные классификаторы позволяют получать высокий результат. Только для этого нужно хорошо настроить классификаторы.
Для улучшения результатов проводится нормировка исходных данных.Все нормировки проводятся по столбцам(можно проводить нормировки и по строкам, но конечные результаты оказываются практически одинаковы). Было испытано 4 различных вида нормировок:
1) По сумме всех значений столбца.
2) По максимальному значению столбца.
3) По среднему значению столбца.
4) По среднему значению ненулевых элементов столбца.
В итоге, самый низкий результат получался при использовании 3-ей нормировки(максимум,который удалось достичь - 0.43). 1-ая и 2-ая нормировки, в итоге, показали примерно одинаковые результаты(максимальное значение в районе 0.49). И самый лучший результат удалось достичь при использовании 4-ой нормировки - 0.513.
После нормировки, необходимо настроить линейные классификаторы. Для настройки применяется кросс-валидация - выборка несколько раз разбивается на две подвыборки: обучающую и контрольную. Алгоритм настраивается по обучающей подвыборке, затем классифицируются объекты контрольной и подсчитывается F-score. Каждому набору параметров ставится в соответстие среднее по всем разбиениям величина F-score на контрольных подвыборках. В итоге, выбирается набор параметров с наилучшей средней оценкой.
И затем строятся 83 классификатора с выбранным набором параметром для независимого решения по каждой тематике, каждый классификатор соответствует одной тематике и отвечает на вопрос "относится/не относится".
Если для некоторого документа классификаторы не выдали ни одного ответа, то в этом случае выдается 5 самых популярных рубрик в тренировочной выборке.
Такой алгоритм получил результат 0.513, и вполне вероятно, что его можно еще улучшить)
Andrew Ostapets 20:50, 19 февраля 2012 (MSK)
Анализ тематик текста
Цель этого раздела — эксперименты с вероятностными моделями тематик в текстах. Задача вероятностной модели — описать, как из скрытых данных (в данном случае это информация о наличии тематики в документе, в каких пропорциях документ содержит тематики) получаются наблюдаемые данные (в данном случае: наличие терминов [слов] в документе, частота термина или его "сила", "вес"). Алгоритмы, которые работают с тематическими моделями, настраивают модель так, чтобы наблюдаемые данные выглядели правдоподобно в рамках модели, а из настроенной модели извлекается нужная информация.
Батя тематических моделей — весьма веселый мужик Prof. David M. Blei. У него есть страница подборкой материалов с по тематическому моделированию. В т.ч. general introduction с описанием идей методов, текст не требует дополнительных знаний о байесовском моделировании, но после него (в принципе) можно успешно использовать весь софт. Еще есть методичка Кропотова с курса БММО: [3], но она для понимания скорее всего потребует чтения [4] и [5].
Модель LDA
LDA (Latent Dirichlet Allocation) — модель смеси тематик, в которой слова формируются следующим образом.
Пусть есть D документов, T тематик, для документа d известно, что он содержит Nd слов. Для каждого документа d:
- Выбирается вектор θd ~ Dir(α), θd = (θd,1, ..., θd,T) из распределения Дирихле, что дает ∑tθd,t=1. Переменная θd,t означает пропорцию, с которой тематика t входит в документ d.
- Для всех слов в документе n = 1..Nd:
- Выбирается тематика слова zd,n, случайно из дискретного распределения с вектором вероятностей θd.
- Выбирается само слово (термин), wd,n из дискретного распределения, заданного вектором вероятностей βt, где t = zd,n (выбранная тематика).
Основным параметром в этой модели являются вектора вероятностей βt, t=1..T. Число βt,w — вероятность того что термином, относящимся к тематике t оказался термин t. Этот параметр (β) собственно и оптимизируется. Еще, как правило, оптимизируется параметр распределения Дирихле (α), еще на вектора β можно навесить априорное распределение Дирихле и их параметры тоже оптимизировать, но это уже детали.
Использование софта с сайта [6]
На радость крестьянину, все эти прожки следуют более-менее одному формату представления данных. Формат прост и описан в readme.txt, а вот скриптик, который переводит матрицу X (из data.mat) в файл с входными данными для lda-c.
Обученная модель состоит из файлов:
- ???.beta: матрица T × W из значений log βt,w.
- ???.other: остальные параметры (число тематик, параметр α, ...)
Файлы со значениями скрытых переменных (z, θ):
- ???.gamma: матрица D × T из значений log q(θd) — логарифма распределения Дирихле (вернее его неточной оценки), которое является апостериорной оценкой параметра θd
- word-assignment.dat: буквально значения z, т.е. соответствия слов тематикам, наверное эта информация достаточно бесполезна.
LDA, вариационный EM-алгоритм
Обученные модели:
- LDA var-EM, 100 topics, raw data, train+test (20K documents) lda100.zip обучалась порядка 10 часов
- LDA var-EM, 200 topics, raw data, train+test (20K documents) lda200.zip обучалась почти ровно сутки :)
Замечание: помимо подхода с вариационным приближением есть подход к обучению LDA методом монте-карло по схеме Гиббса. Какой из подходов лучше зависит от задачи, вряд ли это сможет принципиально улучшить качество категоризации, но есть спортивный интерес.
Модификация LDA для выделения тематик, соответствующих категориям из задачи
Цель: Сделать так, чтобы в ходе настройки тематики выделялись не «с потолка», а именно те, которые соответствуют категориям. Для этого у нас есть информация по каждому документу в виде списка категорий, к которым он относится.
Модификация: В исходной модели, пропорции тематик (θ1, ..., θT) генерируются случайно из распределения Dir(θ1, ..., θT | α). Давайте будем считать, что нам известно, какие тематики в документе присутствуют: t1, ..., ts. Модифицируем исходную модель: будем брать пропорции тематик (θt1, ..., θts) из распределения Dir(θt1, ..., θts | α), а остальные пропорции положим θj = 0 (иных тематик в документе совсем нет).
Более формально: положим известной величину , yd,t = [тематика t содержится в документе d]. Полное правдоподобие модели:
.
Для настройки модели будем максимизировать неполное правдоподобие с условием известной информации о категориях: .
Все формулы для вариационного EM-алгоритма выводятся без принципиальных изменений:
, на
пофиг — они не нужны
— без изменений.
- Здесь t1, ..., ts обозначены тематики, содержащиеся в данном документе, тогда как t'1, ..., t's' — не содержащиеся.
Реализация: код lda-c написан достаточно неплохо, думаю его можно легко модифицировать под новую модель.
Использование новой модели:
- Самое банальное: поставить каждой категории в соответствие тематику, обучать модель с 83 тематиками. Гораздо понятнее, как перевести апостриорные вероятности этих тематик в ответ к нашей задаче.
- Выделение смесей тематик в каждой категории: каждой категории поставить в соответствие K тематик, таким образом модель будет содержать 83·K тематик, после обучения мы будем иметь для каждой категории K апостериорных вероятностей.
Использование моделей для категоризации
Да, да... Это самый полезный вопрос. Давайте подумаем над ним вместе.
Peter Romov 23:25, 14 марта 2012 (MSK)
Сэмплирование Гиббса и его модификация для задачи классификации
Одна из быстрых реализаций метода LDA - это сэмплирование Гиббса. Алгоритм можно посмотреть на слайде(справа).
Будем рассматривать обучение и контроль как единую коллекцию документов. Коллекция частично размечена - мы знаем принадлежности обучающих документов к темам. Такую постановку можно трактовать как задачу с частичным обучением - semi-supervised learning. Все что нужно изменить в GS - это учесть известную информацию в начальных приближениях. Я делала это так:
Длины документов nd - просто суммируем матрицу данных по строкам.
Число слов в документе посвященное теме ntd (для обучения) - 0, если документ не отнесен к этой теме; длина документа делить на число тем, к которым он отнесен по классификации, если отнесен.
Число слов w, относящихся к теме nwt (подсчитанное по обучению) - каждое слово каждого документа распределяем в равных долях по темам, к которым отнесен документ.
Число слов в документе посвященное теме ntd (для контроля) - считаем, что каждое слово документа принадлежит теме t в доле nwt / nw, где nw - сколько всего таких слов в обучении.
Число слов w, относящихся к теме nwt (досчитанное по контролю) - Каждое слово на контроле добавляет к nwt величину nwt / nw, заметим, что распределение слова по темам при этом не меняется.
Число слов в теме nt - просто суммируем матрицу nwt по столбцам.
Далее реализуем описанный на слайде алгоритм. Замечу, что в данном случае длина документа очень велика, поэтому внутренний цикл я вела не по всем словам документа, а по его различным словам, а значит, выбирала единую тему на все вхождений конкретного слова в документ. Это не очень хорошо, потому что обновление счетчиков, связанное с распределением большого числа вхождений одного и того же слова может заметно сказаться на распределении p(t|d) - сместить его. Чтобы этого избежать, стоит разбить внутренний цикл по различным словам на два таких цикла. В первом пересчитывать распределение p(t|w,d), в другом выбирать тему и обновлять счетчики.
Итак, получился алгоритм классификации. Результаты осмысленные, но не очень хорошие - 0.40. Однако это я считала учитывая только первые 4000 признаков из 10000 (ненулевые менее чем на 10 документах отброшены) и всего лишь с 10 сэмплами. Считалось несколько часов. Запустила на 100 сэмплов и по всем признаком - за сутки не посчитала. Надо 1) толково отобрать признаки - princomp, ppca пока упорно отвечают мне out of memory, 2) запустить с бОльшими, но подъемными цифрами и посмотреть, улучшится ли качество.
AnyaP 01:57, 19 марта 2012 (MSK)
Структурный SVM
Не могу больше... выложу PDF.
Peter Romov 03:07, 15 марта 2012 (MSK)
Идеи
- Цепочка независимых классификаторов. Как использовать простую классификацию на два класса, но все таки учитывать зависимости между метками принадлежности тематикам? Например так: принимать решение по тематике 1 исключительно по признакам, решение по тематике 2 принимать по {признакам + принадлежности тематике 1}, …, решение по тематике N принимать по {признакам + решениям о тематиках 1…N-1}. То есть образовать «цепочку» из классификаторов. Peter Romov 21:41, 9 февраля 2012 (MSK)
- Вот, кстати: Liwei et. al., Parallel and Sequential Support Vector Machines for Multi-label Classification. Примерно то, что я имел в виду — простая идея объединения бинарных SVM-ов. Peter Romov 03:27, 15 марта 2012 (MSK)
- Разбиения. Зафиксировать несколько разбиений имеющейся обучающей выборки на тренировочную/тестовую, которую все будут использовать для оценки точности алгоритма. Это может быть полезно так как: 1) он-лайн система тестирования считает качество алгоритма на случайном подмножестве всей тестовой выборки (в правилах написано, что используется ≈10 % объектов), то есть оценка качества может быть неточной; 2) количество попыток отправить ответ на тестовой выборке ограничено 200 попытками, это много, но все же. Peter Romov 21:48, 9 февраля 2012 (MSK)
- Случайное подмножество выбрали до начало конкурса — оно фиксировано для всех отправляющих. nizhibitsky 00:29, 10 февраля 2012 (MSK)
- Терминология, нотация. «метками принадлежности тематикам»… придумать нормальную русскоязычную терминологию и договориться использовать ее, договориться о символьных обозначениях, например
, yj. Peter Romov 21:41, 9 февраля 2012 (MSK)
- Зависимость рубрик. Идея такова: раз это реальные медицинские статьи, то рубрики, к которым они принадлежат, могут быть зависимы (например, статья из рубрики «переломы рук» точно принадлежит рубрике «хирургия»). Для того, чтобы проверить эту гипотезу я посмотрел сколько раз какие две рубрики встречаются вместе для всех статей. и получил следующие результаты (более подробно(а именно таблицу пар) напишу 13 вечером, а то спать хочется=)):
- 1)Из 3403 возможных пар рубрик 2377(69,9 %) пар хотя бы раз встречаются вместе;
- 2)Среди количества одновременных встреч: минимальное 0, максимальное 1278 раз, среднее 27,68 раз. Количеств, больших среднего: 1130(23,8 %).
- Отсюда мысль: если статья принадлежит рубрике A, и есть рубрика B, такая что А и В вместе встречаются очень часто(скажем чаще, чем пороговое k), то наша статья принадлежит и рубрике В. E_zak 03:13, 13 февраля 2012 (MSK)
- Классификация one-vs-one. То есть отделение каждой пары классов друг от друга. Здесь уже нужно n*(n-1)/2 классификаторов. Kondra 23:52, 15 февраля 2012 (MSK)
- Комбинирование результатов алгоритмов. Идея: построить N классификаторов, которые имеют различную природу. В тренировочной выборке на каждый объект приходится чуть менее 4 тем. Настроить классификаторы так, чтобы для каждого объекта они выдавали немного завышенное число тематик. Скажем, порядка 8 тем. В итоге, оставить для каждого объекта только тебе темы, которые выдали хотя бы N/2 классификаторов. Andrew Ostapets 0:44, 19 февраля 2012 (MSK)
- Вычисление оценок. Идея: поскольку матрица сильно разрежена, а признаковое пространство нашей задачи устроено таким образом, что по отдельности признаки неинформативны, но представительные наборы из 2-3 признаков могут обладать хорошей информативностью, то можно попробовать алгоритм КОРА (Вапник или Воронцов). Про формулы оценок принадлежности к классам нормально есть в нашей методичке (или лекции АМА).Матрица бинаризуется по правилу ноль-не-ноль. Выборку по классам можно делить один против всех (получаем 83 независимых алгоритма). Самостоятельно такое решение вряд ли сможет дать хорошие результаты, но в качестве дополнительных признаков в SVM, или внутри Committee Boosting (Воронцов) может оказаться весьма полезным. О результатах экспериментов позже. Berezin 22:09, 21 февраля 2012 (MSK)
- Уменьшение размерности признаков. Machine Learning in Automated Text Categorizatio, FABRIZIO SEBASTIANI. Table I(страница 16). В общем полезная статья о методах классификации текстов. Daria Sergeevna 08:22, 27 февраля 2012 (MSK)
- По поводу уменьшения размерности пространства признаков. Самая простая идея - удалить все нулевые, а затем оставить N самых часто встречаемых. N находим из соображений - работает не больше 5 минут где то (или кому сколько не жалко), ну и на качество смотрим. Ekaterina 23:18, 27 февраля 2012 (MSK)
- Метод ближайшего соседка с весами По классификации текстов должен работать достаточно неплохо метод ближайших соседей, но он выдает около , что судя по турнирной таблице не слишком эффективный вариант. Стоит попробовать метод ближайшего соседа с весовыми коэффициентами. Ekaterina 23:58, 27 февраля 2012 (MSK)
- А тестовые алгоритмы нам не помогут? Хотя тут единиц мало, а признаков и объектов много, но все-таки? Я пока не додумал, у кого-то есть мысли? Kuraga 18:46, 28 февраля 2012 (MSK)
- Отбор признаков. Поскольку пишу уже достаточно долго и не успеваю отладить выкладываю свои наброски генетического алгоритма отбора признаков
function feature_subset=genetic_feature_selection(X,Y, training_method, prediction_method,evaluating, n_population, n_iterations,n_cv) %Genetic algorhytm for feature selection % %feature_subset=genetic_feature_selection( % X,Y, training_method, prediction_method, % evaluating,n_population, n_iterations,n_cv %) % %X - Object-Feature matrix %Y - Classification labels %traning_method(X,Y) - function returning model for %prediction method %prediction_method(X,Y,model) - prediction function %evaluating(Y,A) - function evaluating classification result %Y - predicted labels, A - real labels %n_popunation - number of spicies in population %n_iterations - number of iterations %n_cv - number of folds for cross-validation % %WARNING: n_popunation must be odd %WARNING: fscore(res,Y) - f-measure function must be in path %to use this algorhytm %initial population population=rand(n_population,size(X,2))>0.5; for(i=1:n_iterations) %n life cycles %crossover operator pairs=randperm(n_population); %will be used to determine pairs position=fix(rand()*size(population,2))+1; % selecting crossover position new_spicies=population; new_spicies(pairs(1:2:n_population),1:position)=population(pairs(2:2:n_population),1:position); new_spicies(pairs(2:2:n_population),position:end)=population(pairs(1:2:n_population),position:end); %mutations %mutation probability is 1% mutation_positions=rand(size(population,1),size(population,2))<0.01; new_spicies(mutation_positions)=~new_spicies(mutation_positions); %select spicies %will use f-measure all_pop=[population;new_spicies]; qual=zeros(2*n_population,1); for(cv=1:n_cv) fold=[(cv-1)*size(X,1)/cv+1:cv*size(X,1)/cv]; Xtr=X(setdiff(1:size(X,1),fold),:); Ytr=Y(setdiff(1:size(X,1),fold),:); Xts=X(fold,:); Yts=Y(fold,:); for(j=1:2*n_population) model=training_method(Xtr(:,all_pop(j,:)),Ytr); predicted=prediction_method(Xts(:,all_pop(j,:)),Yts,model); qual(j)=qual(j)+ evaluating(predicted,Yts); end end if(~any(qual)) error('evaluating=0 for all spicies'); end %actually it's better to make qual=qual./n_cv but we don't use exact value [~,ind]=sort(qual,'descend'); population=all_pop(ind(1:n_population),:); end; %return best subset feature_subset=population(1,:); end
Инструменты
LIBLINEAR
LIBLINEAR — библиотека с алгоритмами линейной классификации. Отличается тем, что может работать с очень большими матрицами объект-признак достаточно быстро, может справляться с разреженными матрицами объект-признак, которые в полном объеме не помещаются в память.
Подготовка к использованию с MATLAB. Нужно скачать архив, распаковать его, пользователям не-windows прочитать README и собрать MEX-файлы. Затем в матлабе нужно добавить путь к каталогу с MEX-файлами библиотеки (у пользователей windows это подкаталог liblinear/windows), после чего должны появиться функции train и predict, если их вызвать без параметров, они покажут справочную информацию.
addpath c:/.../liblinear/windows
>> train
Usage: model = train(training_label_vector, training_instance_matrix, 'liblinear_options', 'col');
liblinear_options:
...
>> predict
Usage: [predicted_label, accuracy, decision_values/prob_estimates] = ...
predict(testing_label_vector, testing_instance_matrix, model, 'liblinear_options','col')
liblinear_options:
Обучение модели. Пример: натренируем классификатор, отличающий документы относящиеся к категории 1 от всех остальных.
>> model = train( full(Y(:,1)), X, '-s 3 -c 100 -B 1' )
Функция имеет параметр -v N, который позволяет провести N-fold скользящий контроль, в таком режиме train выдает не модель, а точность классификации на скользящем контроле — это может помочь при настройке параметров.
Классификация. Функции классификации обязательно нужно передавать правильные метки для объектов для того чтобы она посчитала точность классификации, если правильных ответов нет (вы считаете результат на тестовой выборке — нужно сделать вектор из нулей).
>> Y_p(:,1) = predict(zeros(size(X,1), 1), X, model) >> Y_p(:,1) = predict(full(Y(:,k)), X, model) Accuracy = 99.36% (9936/10000)
Peter Romov 11:43, 13 февраля 2012 (MSK)
Проблема у пользователей MSVS
Если после установки библиотеки функции train и predict не вызываются, значит нужно собрать библиотеку вручную.
Делается это просто:
- Делаем текущей папкой c:/.../liblinear/matlab
- Выполняем команду make
- Выполняем команду addpath('c:/.../liblinear/matlab');
Ildar 21:34, 14 февраля 2012 (MSK)
Простенький пример работы с LIBLINEAR
function [Y_t] = classify(X,Y,X_t) Y_t = sparse(size(X_t,1),83); X = bsxfun(@rdivide,X,1500); X_t = bsxfun(@rdivide,X_t,1500); for j = 1:83 model = train( full(Y(:,j)), X); Y_t(:,j) = predict(zeros(size(X_t,1), 1), X_t, model); end h = [ 18 44 40 41 62]; for i = 1:size(Y_t,1) if sum(Y_t(i,:)) == 0 Y_t(i,h) = 1; end end
Пример показывающий, как проводить нормировку и обучать линейный классификатор. Показывает результат в районе 0.43.
Andrew Ostapets 22:13, 29 февраля 2012 (MSK)
R
Для установки языка R (для реализации Random Forest) http://cran.gis-lab.info/
Random Forest http://cran.r-project.org/web/packages/randomForest/index.html
Пособие (минимальное и не факт, что адекваное, по R) http://en.wikibooks.org/wiki/R_Programming
Ekaterina 15:11, 13 февраля 2012 (MSK)
Начало работы с R
Чтобы загрузить данные из Matlab в R можно использовать функцию readMat(filename).
Она находится в пакете R.matlab, чтобы установить его, выполните команду
install.packages("R.matlab")
После установки пакета его нужно загрузить в память, это делается командой
library("R.matlab")
Пример использования:
mat <- readMat('data.mat')
mat$X - обучающая выборка
mat$Y - ответы
Есть также функция writeMat
Novikov 11:39, 27 февраля 2012 (MSK)
Random Forest
Для MATLAB: http://code.google.com/p/randomforest-matlab/
Peter Romov 01:30, 20 февраля 2012 (MSK)
- http://www.stat.berkeley.edu/~breiman/RandomForests/cc_home.htm
- http://alglib.sources.ru/dataanalysis/decisionforest.php
Пакет alglib. Не адаптирован напрямую для МатЛаба. Модификация Random Forest. Random Decision forest. Не так сильно переобучается за счёт коэффициента r - терпимости к шуму. Но! Требует порядка 10 Мб памяти для хранения каждого леса (суммарно - 83*10 Мб, собственно, как и в любом Random Forest). Возможно уменьшение объёмов за счёт уменьшения числа объектов обучения либо уменьшения числа деревьев, либо редукции числа ответов.
Daria Sergeevna 08:15, 27 февраля 2012 (MSK)
GML AdaBoost Toolbox
GML AdaBoost Toolbox — библиотека с различными реализациями алгоритма AdaBoost.
В качестве "слабых" классификаторов выступают Classification and Regression Trees:Обучение модели. Библиотека работает только с Y={-1,+1} и считает, что в обучающая выборка - это матрица размера D*N, где D - количество признаков, N - количество прецедентов.
Пример: натренируем классификатор, отличающий документы относящиеся к категории 18 от всех остальных по первым 100 признакам.
[l w] = RealAdaBoost(tree_node_w(3),X(:,1:100)',(Y(:,18))'*2-1,5);
Классификация.
Y_t(:,18) = (Classify(l,w,X(:,1:100)')>0)';
Недостаток. AdaBoost работает очень медленно при большом количестве признаков, поэтому вначале целесообразно уменьшить количество признаков, и лишь затем запускать сам алгоритм.
Andrew Ostapets 3:10, 22 февраля 2012 (MSK)
Weka. RapidMiner. Mulan
Экспорт из MatLab в ARFF/XML (для Weka, RapidMiner, Mulan)
function arff(X,Y,arffname,xmlname) fid=fopen(arffname,'w'); fprintf(fid,'@relation JRS2012\n'); fprintf(fid,'@attribute Att%d numeric\n',1:size(X,2)); fprintf(fid,'@attribute Class%d {0,1}\n',1:size(Y,2)); fprintf(fid,'@data\n'); for i=1:size(X,1) I=find(X(i,:)); fprintf(fid,'{'); fprintf(fid,'%d %d, ',[I-1;full(X(i,I))]); fprintf(fid,'%d %d, ',[size(X,2)-1+(1:size(Y,2)-1);full(Y(i,1:end-1))]); fprintf(fid,'%d %d}',size(X,2)+size(Y,2)-1,full(Y(i,end))); fprintf(fid,'\n'); end fclose(fid); fid=fopen(xmlname,'w'); fprintf(fid,'<?xml version="1.0" encoding="utf-8"?>\n'); fprintf(fid,'<labels xmlns="http://mulan.sourceforge.net/labels">\n'); fprintf(fid,' <label name=\"Class%d\"></label>\n',1:size(Y,2)); fprintf(fid,'</labels>\n'); fclose(fid);
Novikov 17:37, 27 февраля 2012 (MSK)
- Переделал для multilabel. nizhibitsky 21:45, 28 февраля 2012 (MSK)
Weka: Проблема нехватки памяти
Если вы столкнулись с проблемой "Not enough memory", то при запуске следует указать параметр:
weka -m <N>m
где <N> указывает память в мегабайтах, которую следует выделить, по умолчанию - 256.
Kuraga 20:22, 27 февраля 2012 (MSK)
RapidMiner: Видеоуроки
http://www.youtube.com/playlist?list=UUMT15FE-CnaFCXIxidapVrQ
Kuraga 13:48, 29 февраля 2012 (MSK)
SHOGUN
SHOGUN — пакет с открытым исходным кодом, реализующий множество алгоритмов и структур данных, используемых в data mining.[1] В основном речь идет об SVM, сводную таблицу смотрите на главной странице пакета.
Установка.
- В deb-системах есть пакеты с префиксом shogun-. Для Octave я поставил shogun-octave, shogun-cmdline, shogun-doc.
- В Windows надо компилировать, готового бинарника я не нашел. Описано здесь: [9].
- Также существуют биндинги к очень многим языкам.
Проверка.
- Можете запустить shogun — командную строку.
- В MatLab'e набираем
sg('syntax_highlight','OFF') % возможно, ваш MatLab не понимает раскраски символов - этим вы отключите ее на текущий сеанс. sg('help') sg('help', '<command_or_topic>'))
Документация http://shogun-toolbox.org/doc/en/latest/staticoctave.html
Kuraga 14:36, 29 февраля 2012 (MSK)
Отчеты
Публикуем здесь наши отчеты.
Куракин Александр
Сам я вряд ли чем-то помог группе, кроме того, что немного описал о Shogun'е, и то, о нем мне Петр рассказал. Хотя с его помощью можно было просто реализовать многие вещи — каждый мог этим воспользоваться.
Мне помогли: Петр Ромов, Евгений Нижибицкий, Андрей Остапец, Дмитрий Кондрашкин, Аня Потапенко, Максим Новиков.
Малышева Екатерина
Потапенко Анна
Любимцева Мария
Фонарев Александр
Исмагилов Тимур
Огнева Дарья
Нижибицкий Евгений
Кондрашкин Дмитрий
Остапец Андрей
Китаец Зак Евгений
Лобачева Екатерина
Дьяконов Александр
Гавриков Михаил
Шаймарданов Ильдар
Березин Алексей
отчёт Berezin 16:04, 9 апреля 2012 (MSD)
Новиков Максим
отчёт Novikov 17:04, 9 апреля 2012 (MSD)
Морозова Дарья
[12] Morozova 18:38, 9 апреля 2012 (MSD)
Пакет R
Распределение по пакетам
| № п/п | Студент | Пакет |
|---|---|---|
| 2 | Березин Алексей Андреевич | LogicForest |
| 3 | Борисов Михаил Викторович | tm |
| 4 | Гавриков Михаил Игоревич | mathgraph |
| 5 | Зак Евгений Михайлович | RWeka |
| 6 | Исмагилов Тимур Ниязович | Boruta |
| 7 | Кондрашкин Дмитрий Андреевич | [] |
| 8 | Куракин Александр Владимирович | lasso2 |
| 9 | Лобачева Екатерина Максимовна | ROCR |
| 10 | Любимцева Мария Михайловна | nnet |
| 11 | Малышева Екатерина Константиновна | liblinearR |
| 12 | Морозова Дарья Юрьевна | rminer |
| 13 | Нижибицкий Евгений Алексеевич | [] |
| 14 | Новиков Максим Сергеевич | randomForest |
| 15 | Огнева Дарья Сергеевна | arules |
| 16 | Остапец Андрей Александрович | [] |
| 17 | Потапенко Анна Александровна | [] |
| 18 | Ромов Петр Алексеевич | bnlearn, shogun_modular |
| 19 | Фонарев Александр Юрьевич | gbm |
| 20 | Шаймарданов Ильдар Рифарович | LDA |
Отчеты
Малышева Екатерина
Куракин Александр
Kuraga 21:15, 20 апреля 2012 (MSD)