Прогнозирование функциями дискретного аргумента (пример)

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
Текущая версия (10:00, 26 сентября 2011) (править) (отменить)
(→Литература)
 
(46 промежуточных версий не показаны.)
Строка 2: Строка 2:
==Введение==
==Введение==
-
В отчете представлена попытка прогнозирования таких специфических временных рядов, как монофонические мелодии. Были осуществлены три различных подхода: [[экспоненциальное сглаживание]], локальное прогнозирование и поиск постоянных закономерностей.
+
В статье представлена попытка прогнозирования таких специфических временных рядов, как монофонические мелодии. Были осуществлены три различных подхода: [[экспоненциальное сглаживание]], локальное прогнозирование и поиск постоянных закономерностей.
Предлагается опробовать первый метод в традиционной его форме, чтобы ответить на вопрос, пригоден ли он для решения данной задачи. Затем предлагается во втором методе проверить работоспособность коэффициента корреляции Пирсона в качестве меры сходства. Третий будет использоваться в упрощенном варианте.
Предлагается опробовать первый метод в традиционной его форме, чтобы ответить на вопрос, пригоден ли он для решения данной задачи. Затем предлагается во втором методе проверить работоспособность коэффициента корреляции Пирсона в качестве меры сходства. Третий будет использоваться в упрощенном варианте.
 +
 +
==Постановка задачи==
 +
 +
Мелодия есть функция <tex>m: \ T \rightarrow X\times Y</tex>, где <tex>T = 0, 1, 2, ...</tex> — позиция ноты, <tex>X = 0, 1, 2, ...</tex> — конечное множество нот, занумерованных в порядке увеличения тона, <tex>Y</tex> — длительность ноты, в секундах. Таким образом, будем работать с пучком из двух временных рядов.
 +
 +
Предполагается, что мелодия дана законченная, но без нескольких финальных нот(в данной статье одной). Необходимо их предсказать.
 +
 +
==Пути решения задачи==
 +
 +
<b><big>Экспоненциальное сглаживание</big></b>
 +
 +
Пусть <tex>X=\{x_1, ... x_T\}</tex> — временной ряд.
 +
 +
Экспоненциальное сглаживание ряда осуществляется по рекуррентной формуле:
 +
<tex>
 +
S_t=\alpha x_t + \left( 1-\alpha \right) S_{t-1},\ \alpha \in (0,1).
 +
</tex>
 +
 +
Чем меньше <tex>\alpha</tex>, тем в большей степени фильтруются, подавляются колебания исходного ряда и шума. Если последовательно использовать рекуррентное это соотношение, то экспоненциальную среднюю <tex>S_t</tex> можно выразить через значения временного ряда <tex>X</tex>.
 +
<tex>
 +
S_t =\alpha x_t + (1-\alpha)\left( \alpha x_{t-1} + (1-\alpha)S_{t-2}\right)= \cdot\cdot\cdot = \alpha \sum_{i=0}^{t-1} (1-\alpha)^i x_{t-i} + (1-\alpha)^t S_0.
 +
</tex>
 +
 +
После появления работ Р. Брауна экспоненциальное сглаживание часто используется для решения задачи краткосрочного прогнозирования временных рядов следующим способом. Пусть задан временной ряд: <tex>y_i \cdot\cdot\cdot y_t,\; y_i \in R</tex>.
 +
Необходимо решить задачу прогнозирования временного ряда, т.е. найти
 +
 +
<tex>\hat{y}_{t+d}=f_{t,d}\left(y_{1} ... y_{t} \right),\; d \in \{1,2, ... D\},\; D</tex> — горизонт прогнозирования, необходимо, чтобы
 +
 +
<tex>Q_T=\sum_{i=1}^T \left( y_i-\hat{y}_i \right) \rightarrow \min</tex>.
 +
 +
Предположим, что D - невелико (краткосрочный прогноз), то для решения такой задачи используют модель Брауна.
 +
<tex>\hat{y}_{t+d}=\alpha y_t + ( 1-\alpha ) \hat{y}_t,\; \hat{y}_0 = y_0,\; \alpha \in (0,1)</tex>.
 +
Если рассматривать прогноз на 1 шаг вперед, то <tex>\left(y_t - \hat{y}_t\right)</tex> — погрешность этого прогноза, а новый прогноз <tex>\hat{y}_{t+1}</tex> получается в результате корректировки предыдущего прогноза с учетом его ошибки — суть адаптации.
 +
 +
При краткосрочном прогнозировании желательно как можно быстрее отразить новые изменения и в то же время как можно лучше "очистить" ряд от случайных колебаний. Т.о. следует увеличивать вес более свежих наблюдений:
 +
<tex>
 +
\alpha \rightarrow 1,\; \hat{y}_{t+d} \rightarrow y_t
 +
</tex>.
 +
С другой стороны, для сглаживания случайных отклонений, <tex>\alpha</tex> нужно уменьшить: <tex> \alpha \rightarrow 0,\; \hat{y}_{t+1} \rightarrow \bar{y}_t</tex>. Т.о. эти два требования находятся в противоречии. Мы будем брать <tex>\alpha</tex> из интервала (0,0.5).
 +
 +
<b><big>Локальные методы прогнозирования</big></b>
 +
 +
Музыкальный временной ряд отличается от обычного хаотического: он почти не хаотичен. В нем встречаются похожие, повторяющиеся и прочие регулярные структуры.
 +
 +
<i>Регулярной структурой</i> назовем кусок временного ряда, обладающий автономностью по отношению к остальному временному ряду, склонный к повторению в немного искаженной форме. Очевидно, что "немного" должно определяться некой функцией близости. В работе использовался вариант коэффициента корреляции Неймана-Пирсона:
 +
<center><tex>k(f,g) = \frac{\int fg}{\sqrt{\int f^2}\cdot\sqrt{\int g^2}},</tex></center>
 +
где интеграл понимается в смысле суммы в силу дискретности функций. Прогноз будет строиться на естественном предположении компактности регулярных структур: у похожих кусков временного ряда должны быть похожие продолжения. Воспользуемся самым простым локальным алгоритмом, который ищет ближайшего соседа к прогнозируемому участку.
 +
 +
<b><big>Поиск постоянных закономерностей</big></b>
 +
 +
Рассмотрим один из подходов к поиску закономерностей в пучках временных рядов, который предполагает отсутствие изменений в закономерностях с течением времени. Для простоты будем рассматривать единственный временной ряд длины <tex>T</tex> вместо пучка.
 +
 +
Маской <tex>\omega</tex> на отрезке назовем булеву строку длины <tex>N</tex> (здесь параметр <tex>N</tex> определяет максимальный отступ по времени). Число единиц в маске <tex>\omega</tex> будем называть весом маски и обозначать <tex>H(\omega)</tex>. Элемент маски, находящийся на <tex>i</tex>-ом месте будем обозначать <tex>\omega(i)</tex> или <tex>\omega_i</tex>. Закономерностью <tex>R</tex> назовем пару <tex>(\omega; f)</tex>, где маска <tex>\omega</tex> указывает на значения ряда, являющиеся аргументами функции <tex>f</tex>, а частично-определенная функция <tex>f</tex> задает зависимость значений целевого ряда от переменных, на которые указывает маска <tex>\omega</tex>.
 +
 +
<center><tex>f: X^{H(\omega)} \rightarrow X\cup\{\lambda\},</tex></center>
 +
где <tex>\lambda</tex> означает, что функция не определена на соответствующем наборе переменных.
 +
 +
Зафиксировав теперь маску <tex>\omega = [1, 1, 1]</tex>, построим множество пар <tex>(\alpha_t, v_t)</tex>, где <tex>\alpha_t = [m(t), m(t+1), m(t+2)]</tex>, а <tex>v_t = m(t+3)<tex>, <tex>t\in\{1, 2, \dots , T-3\}</tex>.
 +
 +
Полученное множество пар записывается в виде таблицы частот <tex>\|\nu_{\alpha, v}\|</tex> с числом строк, равным числу всех возможных наборов из <tex>X^{H(\omega)}=x^3</tex>, и числом столбцов, равным <tex>|X|</tex>. Элемент таблицы частот <tex>\|\nu_{\alpha, v}\| \ (0\le\alpha\le |X|^3-1,\ 0\le v\le |X|-1)</tex> — это число раз, которое значение <tex>v</tex> встречается во входных данных на наборе <tex>\tilde{\alpha}</tex> c номером <tex>\alpha</tex> из <tex>X^3</tex>.
 +
 +
(Предполагается, что наборы расположены в лексикографическом порядке.)
 +
 +
Обозначим
 +
 +
<tex>\nu_{\alpha, max} = \max_{v\in\{1, 2, \dots , |X|-1\}} \nu_{\alpha, v}</tex>
 +
 +
и
 +
 +
<tex>v_{m} = \arg\max_{v\in\{1, 2, \dots , |X|-1\}} \nu_{\alpha, v}</tex>
 +
 +
(в случае, если максимум достигается на нескольких значениях, <tex>v_m</tex> выбирается среди этих значений произвольным образом).
 +
 +
Обозначим также
 +
 +
<tex>\nu_{\alpha, max-1} = \max_{v\in\{1, 2, \dots , |X|-1\}, v\ne v_m} \nu_{\alpha, v}</tex>
 +
 +
и
 +
 +
<tex>\nu_{\alpha} = \sum_{v=0}^{|X|-1}\nu_{\alpha, v}</tex>.
 +
 +
На основе таблицы частот порождается закономерность <tex>(\omega; f)</tex>, где частично-определенная функция <tex>f</tex> задается на каждом наборе <tex>\tilde{\alpha}</tex> из <tex>X^3</tex> следующим образом:
 +
 +
<center><tex>f(\tilde{\alpha}) = \left\{ \begin{array}{ll} v_m,\ if\ \nu_{\alpha, max}-\nu_{\alpha, max-1}\ge k\cdot\nu_{\alpha}\\ \lambda,\ else\end{array} \right.</tex></center>
 +
 +
Здесь символ <tex>\lambda</tex> обозначает отсутствие значения на данном наборе, а <tex>k</tex> — параметр алгоритма, <tex>0 < k < 1</tex>.
 +
 +
== Вычислительный эксперимент ==
 +
 +
На следующих изображениях представлены изначальный временной ряд [[Медиа:Гуси.mid]] и его экспоненциальное сглаживание и тот же временной ряд с уже предсказанной точкой
 +
[[Изображение:Plot1.png‎|Изначальный временной ряд Гуси.mid и его экспоненциальное сглаживание]][[Изображение:Plot2.png‎|Временной ряд с предсказанной точкой]]
 +
 +
Для экспоненциального сглаживания была выбрана <tex>\alpha</tex>, при которой среднеквадратичное отклонение ряда от его сглаживания было минимальным. Это значение оказалось равным <tex>\alpha = 0.4361</tex>. Экспоненциальное сглаживание не справилось с поставленной задачей.
 +
 +
Локальное прогнозирование оказалось успешней. В случае первой мелодии оно не только правильно нашло похожий кусок мелодии и правильно предсказало финальную ноту, но и в случае многократной прогонки алгоритма повторяло последнее предложение мелодии. Результаты работы алгоритма представлены в файлах [[Медиа:out1.mid]] и [[Медиа:out2.mid]].
 +
 +
Для прогнозирования поиском постоянных закономерностей в качестве исследуемой мелодии снова был взят файл [[Медиа:Гуси.mid]]. Метод оказался удачным. Результаты работы алгоритма представлены в файле [[Медиа:out3.mid]].
 +
 +
==Заключение==
 +
 +
В заключение можно сказать, что проделана совсем небольшая работа, но уже точно можно сказать, что экспоненциальное сглаживание не может быть использовано для успешного решения поставленной задачи. Локальные же методы представляются более перспективными в том плане, что на мелодиях, обладающих некими похожими повторяющимися фрагментами, есть смысл использовать именно такие методы. К сожалению, в работе были проделаны исследования лишь с одной метрикой, имеет смысл исследовать поведение других метрик.
 +
 +
 +
Метод поиска постоянных закономерностей оказался также удачным. Тем не менее, я склонен рассматривать это следствием того, что мелодия имела точно повторяющиеся куски. То есть для прогноза был найден идентичный кусок, ранее встречавшийся в мелодии, а в качестве прогноза была просто взята следующая за упомянутым куском нота. В силу малой длины мелодии построенная функция оказалась крайне мало определенной на множестве всевозможных наборов из <tex>X^3</tex>. Возможным выходом из данной ситуации, кроме очевидного увеличения длины известной части мелодии, я полагаю выделение при помощи эксперта либо методами кластеризации примитивных элементов мелодии, дальнейшее ее кодирование в терминах этих примитивов. Этот шаг позволит снизить мощность множества допустимых значений временного ряда, а следовательно и множества всевозможных наборов из него же. И искомая частично-определенная функция будет определен плотнее.
 +
 +
Некую информацию о структуре нашего ряда может дать и [[Выделение периодической компоненты временного ряда (пример)|выделение периодической компоненты временного ряда]].
 +
 +
Необходимый для повторения вычислительного эксперимента код можно найти на сайте:
 +
 +
https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/DiscreteForecasting/
 +
 +
А еще набор интересных работ по теме [[Численные методы обучения по прецедентам (практика, В.В. Стрижов)/Группа 874, весна 2011|здесь]].
 +
 +
== Литература ==
 +
 +
*{{s|Brown, R.G.}}. Smoothing forecasting and prediction of discrete time series / Brown, R.G.---N.Y., 1963.
 +
*{{s|Brown, R.G. and Meyer, R.F.}}. The fundamental theorum of exponential smoothing / Brown, R.G. and Meyer, R.F.---Oper. Res., 1961.
 +
*{{s|Бокс Дж., Дженкинс Г.}}. Анализ временных рядов, прогноз и управление. Том 1 / Бокс Дж., Дженкинс Г.---1969.
 +
*{{s|Е.М.Четыркин}}. Статические методы прогнозирования / Е.М.Четыркин.---Издательство "Статистика", 1977.
 +
*{{s|Николай Филипенков}}. О задачах анализа пучков временных рядов с изменяющимися закономерностями / Николай Филипенков.---2006.
 +
*{{s|Николай Филипенков}}. Об алгоритмах прогнозирования процессов с плавно меняющимися закономерностями / Николай Филипенков.~--2010.
 +
*{{s|Ю.П.Лукашин}}. Адаптивные методы краткосрочного прогнозирования временных рядов / Ю.П.Лукашин.---М.: Финансы и статистика, 2003.
 +
*{{s|James McNames}}. Local Modeling Optimization for Time Series Prediction / James McNames.---European Symposium on Artificial Neural Networks Bruges (Belgium). D-Facto public, 2000.
 +
 +
{{ЗаданиеВыполнено|Егор Будников|В.В.Стрижов|6 сентября 2011|Yegor.Budnikov|Strijov}}
 +
[[Категория:Практика и вычислительные эксперименты]]

Текущая версия

Содержание

Введение

В статье представлена попытка прогнозирования таких специфических временных рядов, как монофонические мелодии. Были осуществлены три различных подхода: экспоненциальное сглаживание, локальное прогнозирование и поиск постоянных закономерностей.

Предлагается опробовать первый метод в традиционной его форме, чтобы ответить на вопрос, пригоден ли он для решения данной задачи. Затем предлагается во втором методе проверить работоспособность коэффициента корреляции Пирсона в качестве меры сходства. Третий будет использоваться в упрощенном варианте.

Постановка задачи

Мелодия есть функция m: \ T \rightarrow X\times Y, где T = 0, 1, 2, ... — позиция ноты, X = 0, 1, 2, ... — конечное множество нот, занумерованных в порядке увеличения тона, Y — длительность ноты, в секундах. Таким образом, будем работать с пучком из двух временных рядов.

Предполагается, что мелодия дана законченная, но без нескольких финальных нот(в данной статье одной). Необходимо их предсказать.

Пути решения задачи

Экспоненциальное сглаживание

Пусть X=\{x_1, ... x_T\} — временной ряд.

Экспоненциальное сглаживание ряда осуществляется по рекуррентной формуле: S_t=\alpha x_t + \left( 1-\alpha \right) S_{t-1},\ \alpha \in (0,1).

Чем меньше \alpha, тем в большей степени фильтруются, подавляются колебания исходного ряда и шума. Если последовательно использовать рекуррентное это соотношение, то экспоненциальную среднюю S_t можно выразить через значения временного ряда X. S_t =\alpha x_t + (1-\alpha)\left( \alpha x_{t-1} + (1-\alpha)S_{t-2}\right)= \cdot\cdot\cdot = \alpha \sum_{i=0}^{t-1} (1-\alpha)^i x_{t-i} + (1-\alpha)^t S_0.

После появления работ Р. Брауна экспоненциальное сглаживание часто используется для решения задачи краткосрочного прогнозирования временных рядов следующим способом. Пусть задан временной ряд: y_i \cdot\cdot\cdot y_t,\; y_i \in R. Необходимо решить задачу прогнозирования временного ряда, т.е. найти

\hat{y}_{t+d}=f_{t,d}\left(y_{1} ... y_{t} \right),\; d \in \{1,2, ... D\},\; D — горизонт прогнозирования, необходимо, чтобы

Q_T=\sum_{i=1}^T \left( y_i-\hat{y}_i \right) \rightarrow \min.

Предположим, что D - невелико (краткосрочный прогноз), то для решения такой задачи используют модель Брауна. \hat{y}_{t+d}=\alpha y_t + ( 1-\alpha ) \hat{y}_t,\; \hat{y}_0 = y_0,\; \alpha \in (0,1). Если рассматривать прогноз на 1 шаг вперед, то \left(y_t - \hat{y}_t\right) — погрешность этого прогноза, а новый прогноз \hat{y}_{t+1} получается в результате корректировки предыдущего прогноза с учетом его ошибки — суть адаптации.

При краткосрочном прогнозировании желательно как можно быстрее отразить новые изменения и в то же время как можно лучше "очистить" ряд от случайных колебаний. Т.о. следует увеличивать вес более свежих наблюдений: \alpha \rightarrow 1,\; \hat{y}_{t+d} \rightarrow y_t . С другой стороны, для сглаживания случайных отклонений, \alpha нужно уменьшить: \alpha \rightarrow 0,\; \hat{y}_{t+1} \rightarrow \bar{y}_t. Т.о. эти два требования находятся в противоречии. Мы будем брать \alpha из интервала (0,0.5).

Локальные методы прогнозирования

Музыкальный временной ряд отличается от обычного хаотического: он почти не хаотичен. В нем встречаются похожие, повторяющиеся и прочие регулярные структуры.

Регулярной структурой назовем кусок временного ряда, обладающий автономностью по отношению к остальному временному ряду, склонный к повторению в немного искаженной форме. Очевидно, что "немного" должно определяться некой функцией близости. В работе использовался вариант коэффициента корреляции Неймана-Пирсона:

k(f,g) = \frac{\int fg}{\sqrt{\int f^2}\cdot\sqrt{\int g^2}},

где интеграл понимается в смысле суммы в силу дискретности функций. Прогноз будет строиться на естественном предположении компактности регулярных структур: у похожих кусков временного ряда должны быть похожие продолжения. Воспользуемся самым простым локальным алгоритмом, который ищет ближайшего соседа к прогнозируемому участку.

Поиск постоянных закономерностей

Рассмотрим один из подходов к поиску закономерностей в пучках временных рядов, который предполагает отсутствие изменений в закономерностях с течением времени. Для простоты будем рассматривать единственный временной ряд длины T вместо пучка.

Маской \omega на отрезке назовем булеву строку длины N (здесь параметр N определяет максимальный отступ по времени). Число единиц в маске \omega будем называть весом маски и обозначать H(\omega). Элемент маски, находящийся на i-ом месте будем обозначать \omega(i) или \omega_i. Закономерностью R назовем пару (\omega; f), где маска \omega указывает на значения ряда, являющиеся аргументами функции f, а частично-определенная функция f задает зависимость значений целевого ряда от переменных, на которые указывает маска \omega.

f: X^{H(\omega)} \rightarrow X\cup\{\lambda\},

где \lambda означает, что функция не определена на соответствующем наборе переменных.

Зафиксировав теперь маску \omega = [1, 1, 1], построим множество пар (\alpha_t, v_t), где \alpha_t = [m(t), m(t+1), m(t+2)], а v_t = m(t+3)<tex>, <tex>t\in\{1, 2, \dots , T-3\}.

Полученное множество пар записывается в виде таблицы частот \|\nu_{\alpha, v}\| с числом строк, равным числу всех возможных наборов из X^{H(\omega)}=x^3, и числом столбцов, равным |X|. Элемент таблицы частот \|\nu_{\alpha, v}\| \ (0\le\alpha\le |X|^3-1,\ 0\le v\le |X|-1) — это число раз, которое значение v встречается во входных данных на наборе \tilde{\alpha} c номером \alpha из X^3.

(Предполагается, что наборы расположены в лексикографическом порядке.)

Обозначим

\nu_{\alpha, max} = \max_{v\in\{1, 2, \dots , |X|-1\}} \nu_{\alpha, v}

и

v_{m} = \arg\max_{v\in\{1, 2, \dots , |X|-1\}} \nu_{\alpha, v}

(в случае, если максимум достигается на нескольких значениях, v_m выбирается среди этих значений произвольным образом).

Обозначим также

\nu_{\alpha, max-1} = \max_{v\in\{1, 2, \dots , |X|-1\}, v\ne v_m} \nu_{\alpha, v}

и

\nu_{\alpha} = \sum_{v=0}^{|X|-1}\nu_{\alpha, v}.

На основе таблицы частот порождается закономерность (\omega; f), где частично-определенная функция f задается на каждом наборе \tilde{\alpha} из X^3 следующим образом:

f(\tilde{\alpha}) = \left\{ \begin{array}{ll} v_m,\ if\ \nu_{\alpha, max}-\nu_{\alpha, max-1}\ge k\cdot\nu_{\alpha}\\ \lambda,\ else\end{array} \right.

Здесь символ \lambda обозначает отсутствие значения на данном наборе, а k — параметр алгоритма, 0 < k < 1.

Вычислительный эксперимент

На следующих изображениях представлены изначальный временной ряд Медиа:Гуси.mid и его экспоненциальное сглаживание и тот же временной ряд с уже предсказанной точкой Изначальный временной ряд Гуси.mid и его экспоненциальное сглаживаниеВременной ряд с предсказанной точкой

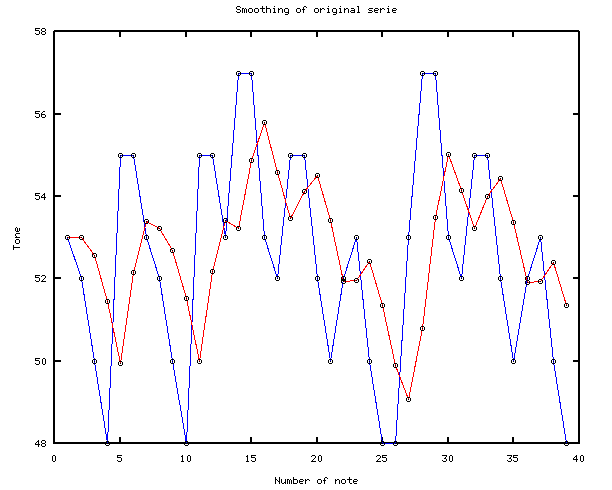
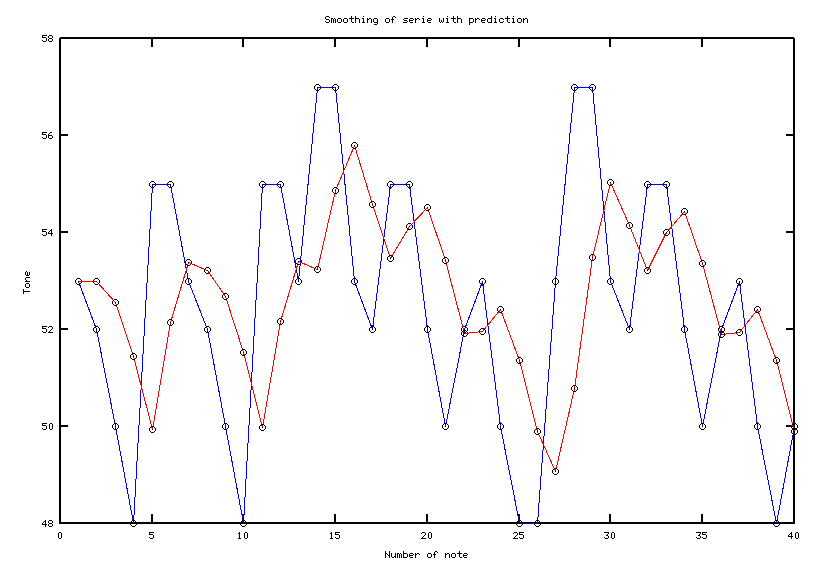
Для экспоненциального сглаживания была выбрана \alpha, при которой среднеквадратичное отклонение ряда от его сглаживания было минимальным. Это значение оказалось равным \alpha = 0.4361. Экспоненциальное сглаживание не справилось с поставленной задачей.

Локальное прогнозирование оказалось успешней. В случае первой мелодии оно не только правильно нашло похожий кусок мелодии и правильно предсказало финальную ноту, но и в случае многократной прогонки алгоритма повторяло последнее предложение мелодии. Результаты работы алгоритма представлены в файлах Медиа:out1.mid и Медиа:out2.mid.

Для прогнозирования поиском постоянных закономерностей в качестве исследуемой мелодии снова был взят файл Медиа:Гуси.mid. Метод оказался удачным. Результаты работы алгоритма представлены в файле Медиа:out3.mid.

Заключение

В заключение можно сказать, что проделана совсем небольшая работа, но уже точно можно сказать, что экспоненциальное сглаживание не может быть использовано для успешного решения поставленной задачи. Локальные же методы представляются более перспективными в том плане, что на мелодиях, обладающих некими похожими повторяющимися фрагментами, есть смысл использовать именно такие методы. К сожалению, в работе были проделаны исследования лишь с одной метрикой, имеет смысл исследовать поведение других метрик.


Метод поиска постоянных закономерностей оказался также удачным. Тем не менее, я склонен рассматривать это следствием того, что мелодия имела точно повторяющиеся куски. То есть для прогноза был найден идентичный кусок, ранее встречавшийся в мелодии, а в качестве прогноза была просто взята следующая за упомянутым куском нота. В силу малой длины мелодии построенная функция оказалась крайне мало определенной на множестве всевозможных наборов из X^3. Возможным выходом из данной ситуации, кроме очевидного увеличения длины известной части мелодии, я полагаю выделение при помощи эксперта либо методами кластеризации примитивных элементов мелодии, дальнейшее ее кодирование в терминах этих примитивов. Этот шаг позволит снизить мощность множества допустимых значений временного ряда, а следовательно и множества всевозможных наборов из него же. И искомая частично-определенная функция будет определен плотнее.

Некую информацию о структуре нашего ряда может дать и выделение периодической компоненты временного ряда.

Необходимый для повторения вычислительного эксперимента код можно найти на сайте:

https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/DiscreteForecasting/

А еще набор интересных работ по теме здесь.

Литература

  • Brown, R.G.. Smoothing forecasting and prediction of discrete time series / Brown, R.G.---N.Y., 1963.
  • Brown, R.G. and Meyer, R.F.. The fundamental theorum of exponential smoothing / Brown, R.G. and Meyer, R.F.---Oper. Res., 1961.
  • Бокс Дж., Дженкинс Г.. Анализ временных рядов, прогноз и управление. Том 1 / Бокс Дж., Дженкинс Г.---1969.
  • Е.М.Четыркин. Статические методы прогнозирования / Е.М.Четыркин.---Издательство "Статистика", 1977.
  • Николай Филипенков. О задачах анализа пучков временных рядов с изменяющимися закономерностями / Николай Филипенков.---2006.
  • Николай Филипенков. Об алгоритмах прогнозирования процессов с плавно меняющимися закономерностями / Николай Филипенков.~--2010.
  • Ю.П.Лукашин. Адаптивные методы краткосрочного прогнозирования временных рядов / Ю.П.Лукашин.---М.: Финансы и статистика, 2003.
  • James McNames. Local Modeling Optimization for Time Series Prediction / James McNames.---European Symposium on Artificial Neural Networks Bruges (Belgium). D-Facto public, 2000.


Данная статья была создана в рамках учебного задания.
Студент: Егор Будников
Преподаватель: В.В.Стрижов
Срок: 6 сентября 2011


В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://recognition.su/wiki/index.php?title=%D0%9F%D1%80%D0%BE%D0%B3%D0%BD%D0%BE%D0%B7%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F%D0%BC%D0%B8_%D0%B4%D0%B8%D1%81%D0%BA%D1%80%D0%B5%D1%82%D0%BD%D0%BE%D0%B3%D0%BE_%D0%B0%D1%80%D0%B3%D1%83%D0%BC%D0%B5%D0%BD%D1%82%D0%B0_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»