Методы прямоугольников и трапеций
Материал из MachineLearning.
(→Формула трапеций) |
|||
| (22 промежуточные версии не показаны) | |||
| Строка 1: | Строка 1: | ||
== Введение == | == Введение == | ||
| - | + | [[Изображение:Integral.png|thumb|200px|Рис.1]] | |
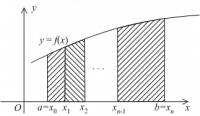
Задача численного интегрирования состоит в нахождении приближенного значения интеграла | Задача численного интегрирования состоит в нахождении приближенного значения интеграла | ||
| - | + | ||
{{ eqno | 1 }} | {{ eqno | 1 }} | ||
| - | <p align="center"><tex> | + | <p align="center"><tex>I=\int_a^b{f(x)dx},</tex></p> |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | где <tex>f(x)</tex> - заданная и интегрируемая на отрезке <tex>[a,b]</tex> функция. | |
| - | + | Если один или оба предела равны <tex>+ \infty</tex> или <tex>- \infty</tex>, то с помощью трюков с заменой переменных можно осуществить переход к конечному отрезку от луча или всей числовой прямой. | |
| - | Введем на <tex>[a,b]</tex> | + | Введем на <tex>[a,b]</tex> сетку с переменным шагом <tex>h_i</tex>, т.е. множество точек <tex>\omega_h=\{x_i=a+\sum_{j=0}^i{h_j}, i=0,1,...,N,h_0=0, \sum_{i=1}^N{h_i}=b-a}</tex>, и представим интеграл {{eqref|1}} в виде суммы интегралов по частичным отрезкам: |
{{ eqno | 3 }} | {{ eqno | 3 }} | ||
<p align="center"><tex>\int_a^b{f(x)dx}=\sum_{i=1}^N{\int_{x_{i-1}}^{x_i}{f(x)dx}}.</tex></p> | <p align="center"><tex>\int_a^b{f(x)dx}=\sum_{i=1}^N{\int_{x_{i-1}}^{x_i}{f(x)dx}}.</tex></p> | ||
| - | Для построения формулы численного интегрирования на | + | Для построения формулы численного интегрирования на всем отрезке <tex>[a,b]</tex> достаточно построить квадратурную формулу для интеграла |
{{ eqno | 4 }} | {{ eqno | 4 }} | ||
| Строка 33: | Строка 24: | ||
на частичном отрезке <tex>[x_{i-1},x_i]</tex> и воспользоваться свойством {{eqref|3}}. | на частичном отрезке <tex>[x_{i-1},x_i]</tex> и воспользоваться свойством {{eqref|3}}. | ||
| - | == | + | == Метод прямоугольников == |
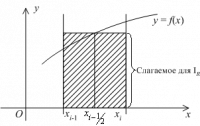
| - | === Формула прямоугольников === | + | === Формула прямоугольников на частичном отрезке и ее погрешность === |
| + | |||
| + | [[Изображение:Integral_rect.png|thumb|200px|Рис.2]] | ||
Заменим интеграл {{eqref|3}} выражением <tex>f(x_{i-1/2})h</tex>, где <tex>x_{i-1/2}=x_{i}-0.5h.</tex> | Заменим интеграл {{eqref|3}} выражением <tex>f(x_{i-1/2})h</tex>, где <tex>x_{i-1/2}=x_{i}-0.5h.</tex> | ||
| - | + | Тогда получим формулу | |
{{ eqno | 5 }} | {{ eqno | 5 }} | ||
| Строка 63: | Строка 56: | ||
<p align="center"><tex>\psi_{i}=\int_{x_{i-1}}^{x_i}{\frac{(x-x_{i-1/2})^2}{2}f''(\xi_i)dx}</tex></p> | <p align="center"><tex>\psi_{i}=\int_{x_{i-1}}^{x_i}{\frac{(x-x_{i-1/2})^2}{2}f''(\xi_i)dx}</tex></p> | ||
| - | Обозначая <tex>M_{2,i}=\underset{x\in [x_{i-1},x_i]}{max}|f''(x)|</tex>, оценим <tex>\ | + | Обозначая <tex>M_{2,i}=\underset{x\in [x_{i-1},x_i]}{max}|f''(x)|</tex>, оценим <tex>\psi_i</tex> следующим образом: |
| - | <p align="center"><tex>|\ | + | <p align="center"><tex>|\psi_i|\le M_{2,i} \int_{x_{i-1}}^{x_i}{\frac{(x-x_{i-1/2})^2}{2}dx}=\frac{h^3}{24}M_{2,i}</tex></p> |
Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива оценка | Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива оценка | ||
{{ eqno | 7 }} | {{ eqno | 7 }} | ||
| - | <p align="center"><tex>|\ | + | <p align="center"><tex>|\psi_i|\le \frac{h^3}{24}M_{2,i}</tex></p> |
т.е. формула имеет погрешность <tex>O(h^3)</tex> при <tex>h\rightarrow0</tex>. | т.е. формула имеет погрешность <tex>O(h^3)</tex> при <tex>h\rightarrow0</tex>. | ||
| - | Заметим,что оценка | + | Заметим,что оценка {{eqref|7}} является неулучшаемой, т.е. существует функция <tex>f(x)</tex>, для которой {{eqref|7}} выполняется со знаком равенства. Действительно, для <tex>f(x)=(x-x_{i-1/2})^2</tex> имеем <tex>M_{2,i}=2, f(x_{i-1/2})=0</tex> и |
<p align="center"><tex>\int_{x_{i-1}}^{x_i}{f(x)dx}-f(x_{i-1/2})h=\frac{h^3}{24}M_{2,i}</tex></p> | <p align="center"><tex>\int_{x_{i-1}}^{x_i}{f(x)dx}-f(x_{i-1/2})h=\frac{h^3}{24}M_{2,i}</tex></p> | ||
| - | Суммируя равенства | + | === Составная формула прямоугольников и ее погрешность === |
| + | |||
| + | Суммируя равенства {{eqref|5}} по <tex>i</tex> от <tex>1</tex> до <tex>N</tex>, получим ''составную формулу прямоугольников'' | ||
{{ eqno | 8 }} | {{ eqno | 8 }} | ||
| Строка 98: | Строка 93: | ||
т.е. погрешность формулы прямоугольников на всем отрезке есть велицина <tex>O(h^2)</tex>. | т.е. погрешность формулы прямоугольников на всем отрезке есть велицина <tex>O(h^2)</tex>. | ||
| - | + | Видим, что квадратурная формула имеет ''второй порядок точности''. | |
| - | === Формула трапеций === | + | === Применимость метода к функции, заданной в конечном числе точек === |
| + | |||
| + | Заметим, что метод прямоугольников в том виде,в котором он описан выше, не применим в общем случае к функциям,значения которых мы знаем в конечном числе точек, так как, например, мы не всегда можем разбить отрезкок интегрирования на подотрезки, серединами которых являются точки,в которых нам известно значение функции. | ||
| + | |||
| + | == Метод трапеций == | ||
| + | |||
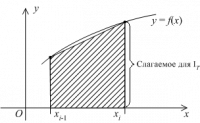
| + | === Формула трапеций на частичном отрезке и ее погрешность === | ||
| + | |||
| + | [[Изображение:Integral_trap.png|thumb|200px|Рис.3]] | ||
На частичном отрезке эта формула имеет вид | На частичном отрезке эта формула имеет вид | ||
| Строка 124: | Строка 127: | ||
<p align="center"><tex>|\psi_i|\le \frac{M_{2,i}h^3}{12}</tex></p> | <p align="center"><tex>|\psi_i|\le \frac{M_{2,i}h^3}{12}</tex></p> | ||
| - | Оценка | + | Оценка {{eqref|11}} неулучшаема, так как в ней достигается равенство, например, для <tex>f(x)=(x-x_i)^2</tex>. |
| + | |||
| + | === Составная формула трапеций и ее погрешность === | ||
''Составная формула трапеций'' имеет вид | ''Составная формула трапеций'' имеет вид | ||
| Строка 136: | Строка 141: | ||
{{ eqno | 13 }} | {{ eqno | 13 }} | ||
| - | <p align="center"><tex>|\Psi|\le \frac{h^2(b-a)}{12}M_2,M_2=\underset{x\in [a,b]}{max}|f''(x)|</tex | + | <p align="center"><tex>|\Psi|\le \frac{h^2(b-a)}{12}M_2,</tex></p> |
| + | |||
| + | где <tex>M_2=\underset{x\in [a,b]}{max}|f''(x)|</tex> | ||
Таким образом, формула трапеций имеет, так же как и формула прямоугольников, второй порядок точности,<tex>\Psi=O(h^2)</tex>, но ее погрешность оценивается величиной в два раза большей. | Таким образом, формула трапеций имеет, так же как и формула прямоугольников, второй порядок точности,<tex>\Psi=O(h^2)</tex>, но ее погрешность оценивается величиной в два раза большей. | ||
| + | |||
| + | === Применимость метода к функции, заданной в конечном числе точек === | ||
| + | |||
| + | В отличие от метода прямоугольников, метод трапеций применим к функциям, заданным в конечном числе точек, так как мы всегда можем взять в качесве узлов интегрирования данные точки. | ||
== Числовой пример == | == Числовой пример == | ||
Вычислим по формулам прямоугольников и трапеций при <tex>n=2</tex> интеграл | Вычислим по формулам прямоугольников и трапеций при <tex>n=2</tex> интеграл | ||
| - | {{ eqno | | + | {{ eqno | 14 }} |
<p align="center"><tex>I=\int_{0}^{\pi/2}{\sin(x)dx} = 1</tex></p> | <p align="center"><tex>I=\int_{0}^{\pi/2}{\sin(x)dx} = 1</tex></p> | ||
В данном случае | В данном случае | ||
| - | |||
<p align="center"><tex>P_2=\frac{\pi}{4}(\sin(\frac{\pi}{8})+\sin(\frac{3\pi}{8}))=1.026172</tex></p> | <p align="center"><tex>P_2=\frac{\pi}{4}(\sin(\frac{\pi}{8})+\sin(\frac{3\pi}{8}))=1.026172</tex></p> | ||
| Строка 153: | Строка 163: | ||
<p align="center"><tex>T_2=\frac{\pi}{4}(\frac{1}{2}\sin(0)+\sin(\frac{\pi}{4})+\frac{1}{2}\sin(\frac{\pi}{2}))=0.948059</tex></p> | <p align="center"><tex>T_2=\frac{\pi}{4}(\frac{1}{2}\sin(0)+\sin(\frac{\pi}{4})+\frac{1}{2}\sin(\frac{\pi}{2}))=0.948059</tex></p> | ||
| - | Зная точный ответ | + | Зная точный ответ {{eqref|14}}, найдем погрешности |
| - | {{ eqno | | + | {{ eqno | 15 }} |
<p align="center"><tex>\alpha_2=-0.026172,\beta_2=0.051941</tex></p> | <p align="center"><tex>\alpha_2=-0.026172,\beta_2=0.051941</tex></p> | ||
| - | Вторая производная функции <tex>\sin(x)</tex> на отрезке <tex>[0,\pi/2]</tex> отрицательна, ее модуль не превышает единицы: <tex>M_2=1</tex>. Величина погрешностей | + | Вторая производная функции <tex>\sin(x)</tex> на отрезке <tex>[0,\pi/2]</tex> отрицательна, ее модуль не превышает единицы: <tex>M_2=1</tex>. Величина погрешностей {{eqref|15}} удовлетворяет неравенствам {{eqref|9}} и {{eqref|13}}: |
<p align="center"><tex>|\alpha_2|\le \frac{1}{96}(\frac{\pi}{2})^3<0.041,|\beta_2|\le \frac{1}{48}(\frac{\pi}{2})^3<0.081</tex></p> | <p align="center"><tex>|\alpha_2|\le \frac{1}{96}(\frac{\pi}{2})^3<0.041,|\beta_2|\le \frac{1}{48}(\frac{\pi}{2})^3<0.081</tex></p> | ||
== Рекомендации программисту == | == Рекомендации программисту == | ||
| + | |||
| + | === Оценка погрешности === | ||
| + | |||
| + | Величина погрешности численного интегрирования зависит как от шага сетки <tex>h</tex>, так и от гладкости подынтегральной функции <tex>f(x)</tex>. Например, в оценку {{eqref|11}}, наряду с <tex>h</tex>, входит величина | ||
| + | |||
| + | <p align="center"><tex>M_{2,i}=\underset{x\in [x_{i-1},x_i]}{max}|f''(x)|,</tex></p> | ||
| + | |||
| + | которая может сильно меняться от точки к точке и, вообще говоря, заранее неизвестна. Если величина погрешности велика, то ее можно уменьшить путем измельчения сетки на данном отрезке <tex>[x_{i-1},x_i]</tex>. Для этого прежде всего надо уметь апостериорно, т.е. после проведения расчета, оценивать погрешность. | ||
| + | |||
| + | Апостериорную оценку погрешности можно осуществить ''методом Рунге''. Пусть какая-то квадратурная формула имеет на частичном отрезке порядок точности <tex>m</tex>, т.е. <tex>I_i-I_{h,i}\approx c_i h_i^m</tex>. Тогда | ||
| + | |||
| + | <p align="center"><tex>I_i-I_{h/2,i}\approx c_i (\frac{h_i}{2})^m,</tex></p> | ||
| + | |||
| + | откуда получим | ||
| + | |||
| + | {{ eqno | 16 }} | ||
| + | <p align="center"><tex>I_i-I_{h,i}\approx 2^m (I_i-I_{h/2,i}),</tex></p> | ||
| + | |||
| + | {{ eqno | 17 }} | ||
| + | <p align="center"><tex>I_i-I_{h/2,i}\approx \frac{I_{h/2,i}-I_{h,i}}{2^m-1}</tex></p> | ||
| + | |||
| + | Пусть используется составная квадратурная формула | ||
| + | |||
| + | <p align="center"><tex>I\approx I_h=\sum_{i=1}^N{I_{h,i}}</tex></p> | ||
| + | |||
| + | где <tex>I_{h,i}</tex> - квадратурная сумма на частичном отрезке, причем на каждом частичном отрезке используется одна и та же квадратурная формула (например, формула трапеций). Проведем на каждом частичном отрезке <tex>[x_{i-1},x_i]</tex> все вычисления дважды, один раз - с шагом <tex>h_i</tex> и второй раз - с шагом <tex>0.5h_i</tex> и оценим погрешность по правилу Рунге {{eqref|17}}: | ||
| + | |||
| + | <p align="center"><tex>\Psi = |I-I_{h/2}|\approx \sum_{i=1}^N{|I_i-I_{h/2,i}|}=\frac{|I_{h/2}-I_{h}|}{2^m-1}.</tex></p> | ||
| + | |||
| + | === Пример программы на языке C++ === | ||
| + | |||
| + | * [[Media:Integral.zip|Исходный текст программы]] | ||
| + | |||
| + | В программе интеграруемая функция задается в функции <tex>function</tex>. В данном примере интегрируется логарифм и эта функция выглядит так: | ||
| + | |||
| + | <pre> | ||
| + | double function(double x) | ||
| + | { | ||
| + | return log(x); | ||
| + | } | ||
| + | </pre> | ||
| + | |||
| + | Функция <tex>rectangles</tex> реализует метод прямоугольников, а <tex>trapezium</tex> - метод трапеций. | ||
| + | |||
| + | Эти функции имеют следующие параметры: | ||
| + | |||
| + | <pre> | ||
| + | double trapezium(double left, double right, double step) | ||
| + | double rectangles(double left, double right, double step) | ||
| + | |||
| + | где left - левый предел интегрирования, | ||
| + | right - правй предел интегрирования, | ||
| + | step - шаг интегрирования. | ||
| + | </pre> | ||
| + | |||
== Заключение == | == Заключение == | ||
| + | |||
| + | Методы прямоугольников и трапеций являются одними из простейших методов интегрирования (запрограммировать их не составляет особого труда). Но эти методы имеют лишь второй порядок точности,в то время как есть методы более высоких порядков. | ||
| + | |||
| + | Если же сравнивать эти два метода между собой, то метод прямоугольников, который относится к методам Гаусса - Кристоффеля, является точнее метода трапеций, относящегося к методам Ньютона - Котеса. Но в то же время метод трапеций может применяться с произвольным шагом, в отличие от метода прямоугольников, который, как мы увидели, не применим, например, к функциям,заданным в конечном числе точек. | ||
| + | |||
== Список литературы == | == Список литературы == | ||
* ''А.А.Самарский, А.В.Гулин.'' Численные методы М.: Наука, 1989. | * ''А.А.Самарский, А.В.Гулин.'' Численные методы М.: Наука, 1989. | ||
| Строка 170: | Строка 240: | ||
{{stub}} | {{stub}} | ||
[[Категория:Численное интегрирование]] | [[Категория:Численное интегрирование]] | ||
| + | [[Категория:Учебные задачи]] | ||
Текущая версия
Содержание |
Введение
Задача численного интегрирования состоит в нахождении приближенного значения интеграла
где - заданная и интегрируемая на отрезке
функция.
Если один или оба предела равны или
, то с помощью трюков с заменой переменных можно осуществить переход к конечному отрезку от луча или всей числовой прямой.
Введем на сетку с переменным шагом
, т.е. множество точек
, и представим интеграл (1) в виде суммы интегралов по частичным отрезкам:
Для построения формулы численного интегрирования на всем отрезке достаточно построить квадратурную формулу для интеграла
на частичном отрезке и воспользоваться свойством (3).
Метод прямоугольников
Формула прямоугольников на частичном отрезке и ее погрешность
Заменим интеграл (3) выражением , где
Тогда получим формулу
которая называется формулой прямоугольников на частичном отрезке
Погрешность метода (5) определяется величиной
которую легко оценить с помощью формулы Тейлора. Действительно, запишем в виде
и воспользуемся разложением
где . Тогда из (6) получим
Обозначая , оценим
следующим образом:
Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива оценка
т.е. формула имеет погрешность при
.
Заметим,что оценка (7) является неулучшаемой, т.е. существует функция , для которой (7) выполняется со знаком равенства. Действительно, для
имеем
и
Составная формула прямоугольников и ее погрешность
Суммируя равенства (5) по от
до
, получим составную формулу прямоугольников
Погрешность этой формулы
равна сумме погрешностей по всем частичным отрезкам,
Отсюда, обозначая , получим
т.е. погрешность формулы прямоугольников на всем отрезке есть велицина .
Видим, что квадратурная формула имеет второй порядок точности.
Применимость метода к функции, заданной в конечном числе точек
Заметим, что метод прямоугольников в том виде,в котором он описан выше, не применим в общем случае к функциям,значения которых мы знаем в конечном числе точек, так как, например, мы не всегда можем разбить отрезкок интегрирования на подотрезки, серединами которых являются точки,в которых нам известно значение функции.
Метод трапеций
Формула трапеций на частичном отрезке и ее погрешность
На частичном отрезке эта формула имеет вид
и получается путем замены подынтегральной функции интерполяционным многочленом первой степени,постоенным по узлам
, т.е. функцией
Для оценки погрешности достаточно вспомнить,что
Отсюда получим
и,следовательно,
Оценка (11) неулучшаема, так как в ней достигается равенство, например, для .
Составная формула трапеций и ее погрешность
Составная формула трапеций имеет вид
где .
Погрешность этой формулы оценивается следующим образом:
где
Таким образом, формула трапеций имеет, так же как и формула прямоугольников, второй порядок точности,, но ее погрешность оценивается величиной в два раза большей.
Применимость метода к функции, заданной в конечном числе точек
В отличие от метода прямоугольников, метод трапеций применим к функциям, заданным в конечном числе точек, так как мы всегда можем взять в качесве узлов интегрирования данные точки.
Числовой пример
Вычислим по формулам прямоугольников и трапеций при интеграл
В данном случае
Зная точный ответ (14), найдем погрешности
Вторая производная функции на отрезке
отрицательна, ее модуль не превышает единицы:
. Величина погрешностей (15) удовлетворяет неравенствам (9) и (13):
Рекомендации программисту
Оценка погрешности
Величина погрешности численного интегрирования зависит как от шага сетки , так и от гладкости подынтегральной функции
. Например, в оценку (11), наряду с
, входит величина
которая может сильно меняться от точки к точке и, вообще говоря, заранее неизвестна. Если величина погрешности велика, то ее можно уменьшить путем измельчения сетки на данном отрезке . Для этого прежде всего надо уметь апостериорно, т.е. после проведения расчета, оценивать погрешность.
Апостериорную оценку погрешности можно осуществить методом Рунге. Пусть какая-то квадратурная формула имеет на частичном отрезке порядок точности , т.е.
. Тогда
откуда получим
Пусть используется составная квадратурная формула
где - квадратурная сумма на частичном отрезке, причем на каждом частичном отрезке используется одна и та же квадратурная формула (например, формула трапеций). Проведем на каждом частичном отрезке
все вычисления дважды, один раз - с шагом
и второй раз - с шагом
и оценим погрешность по правилу Рунге (17):
Пример программы на языке C++
В программе интеграруемая функция задается в функции . В данном примере интегрируется логарифм и эта функция выглядит так:
double function(double x)
{
return log(x);
}
Функция реализует метод прямоугольников, а
- метод трапеций.
Эти функции имеют следующие параметры:
double trapezium(double left, double right, double step)
double rectangles(double left, double right, double step)
где left - левый предел интегрирования,
right - правй предел интегрирования,
step - шаг интегрирования.
Заключение
Методы прямоугольников и трапеций являются одними из простейших методов интегрирования (запрограммировать их не составляет особого труда). Но эти методы имеют лишь второй порядок точности,в то время как есть методы более высоких порядков.
Если же сравнивать эти два метода между собой, то метод прямоугольников, который относится к методам Гаусса - Кристоффеля, является точнее метода трапеций, относящегося к методам Ньютона - Котеса. Но в то же время метод трапеций может применяться с произвольным шагом, в отличие от метода прямоугольников, который, как мы увидели, не применим, например, к функциям,заданным в конечном числе точек.
Список литературы
- А.А.Самарский, А.В.Гулин. Численные методы М.: Наука, 1989.
- А.А.Самарский. Введение в численные методы М.: Наука, 1982.