Эластичная сеть
Материал из MachineLearning.
(Новая: '''Эластичная сеть''' — модель регрессии с двумя регуляризаторами L1, L2. == Определение == Пусть известны ...) |
(→Пример) |
||
| (1 промежуточная версия не показана) | |||
| Строка 1: | Строка 1: | ||
| - | '''Эластичная сеть''' — модель регрессии с двумя регуляризаторами | + | '''Эластичная сеть''' — модель [[Регрессия|регрессии]] с двумя регуляризаторами l1, l2<ref name="elnet"> Zou H., Hastie T. (2005). [http://www.stanford.edu/~hastie/Papers/B67.2%20(2005)%20301-320%20Zou%20&%20Hastie.pdf Regularization and variable selection via the elastic net.] Journal of the Royal Statistical Society, 5(2), 427–320.</ref>. |
== Определение == | == Определение == | ||
| - | Пусть известны измерения n | + | Пусть известны измерения <tex>n</tex> объектов. Каждый объект представим в виде пары <tex>(x_i, y_i)</tex>, <tex> x_i \in \mathbb{R}^k</tex>, <tex> y_i \in \mathbb{R} </tex>. Для удобства будем записывать это в матричном виде: <tex>(X, y) </tex>. [[Многомерная линейная регрессия|Классическая задача регрессии]] ставится следующим образом: |
| + | ::<tex>\left|y - Xw\right|^2 \to \min_w</tex>. | ||
| + | В силу неточности измерений данных или каких либо еще ошибок с целью построения наилучшей модели вводят регуляризатор или несколько регуляризаторов. Тогда получается следующая задача оптимизации: | ||
| + | ::<tex>\left|y - Xw\right|^2_2 + \lambda_1 \left|w\right|_1 + \lambda_2 \left|w\right|^2_2 \to \min_w</tex>. | ||
| + | Частными случаями являются модели [[лассо]] (<tex>\lambda_2 = 0</tex>) и [[Гребневая регрессия|гребневой регрессии]] (<tex>\lambda_1 = 0 </tex>). | ||
| + | Для каждого фиксированного <tex>\lambda_2</tex> можно перебрать все возможные значения параметра <tex>\lambda_1</tex> (поскольку по этому параметру это кусочно-линейная функция с конечным числом точек, в которых она не дифференцируема)<ref name="lars"> Efron B., Hastie T., Johnstone I., Tibshirani R. (2004). [http://statweb.stanford.edu/~imj/WEBLIST/2004/LarsAnnStat04.pdf Least angle regression.] The Annals of Statistics, 32(2), 407–499.</ref>. | ||
== Реализации == | == Реализации == | ||
| + | * Matlab: Функция lasso, для задания l2 регуляризации есть дополнительный аргумент Alpha<ref name="matlab"> [http://www.mathworks.com/help/stats/lasso.html Regularized least-squares regression using lasso or elastic net algorithms]</ref>. | ||
| + | * Python: В пакете sklearn есть библиотека linear_model в которой есть класс ElasticNet<ref name="python"> Пример: [http://scikit-learn.org/0.11/auto_examples/linear_model/plot_lasso_and_elasticnet.html#example-linear-model-plot-lasso-and-elasticnet-py Lasso and Elastic Net for Sparse Signals]</ref>. | ||
| + | * R: Пакет glmnet<ref name="r"> [http://cran.r-project.org/web/packages/glmnet/index.html glmnet: Lasso and elastic-net regularized generalized linear models]</ref>. | ||
| + | Во всех реализациях используется подход [[LARS]], который как раз и позволяет найти все точки перегиба функционала по <tex> \lambda_1</tex>. | ||
| - | + | Также в Matlab и Python есть соответствующие функции для выбора оптимальных значений параметров по кросс-валидации: в Matlab это все та же функция lasso, в Python это класс ElasticNetCV. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | Также в Matlab и Python есть | + | |
==Пример == | ==Пример == | ||
[[Изображение: Lasso_and_elastic_net_example.png]] | [[Изображение: Lasso_and_elastic_net_example.png]] | ||
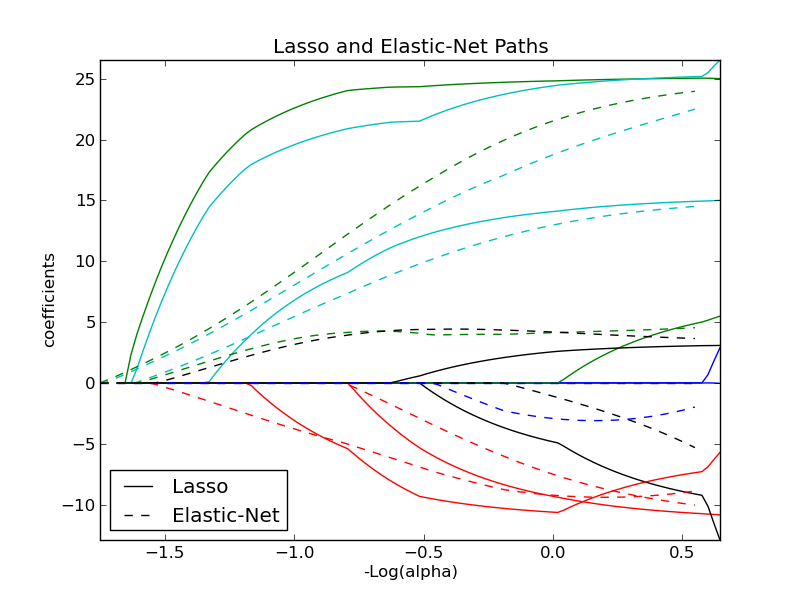
| + | [http://scikit-learn.org/stable/auto_examples/linear_model/plot_lasso_coordinate_descent_path.html#example-linear-model-plot-lasso-coordinate-descent-path-py Пример использования Lasso и ElasticNet] в Python на данных идущих в комплекте с пакетом SkLearn. В данном примере рассматриваются данные о диабетиках. Собраны данные с 442 пациентов у каждого замерено 10 физиологических признаков, среди которых вес, пол, возраст и давление в крови. В качестве целевого признака известна непрерывная величина характеризующая прогрессивность болезни за последний год. Ставится задача предсказания по физиологическим характеристикам человека прогрессивность болезни. Строится две модели <tex>\lambda_2 = 0</tex> (Lasso), <tex>\lambda_2 = 0.7</tex> (Elastic-Net). На графике изображены значения весов обученной модели в зависимости от коэффициента регуляризации <tex>\lambda_1</tex>. По графику видно, что веса признаков в эластичной сети в зависимости от L1 регуляризатора более гладкие по сравнению с лассо. Тем не менее можно заметить, что поведение весов очень похоже. Эластичная сеть не так жестко зануляет коэффициенты, то есть они обнулились только в самой левой точке(очень большой регуляризатор). | ||
| - | |||
== Ссылки == | == Ссылки == | ||
| - | + | <references /> | |
| - | + | ||
| - | + | [[Категория:Линейная регрессия]] | |
| - | + | [[Категория:Регрессионный анализ]] | |
| - | + | ||
| - | + | ||
Текущая версия
Эластичная сеть — модель регрессии с двумя регуляризаторами l1, l2[1].
Содержание |
Определение
Пусть известны измерения объектов. Каждый объект представим в виде пары
,
,
. Для удобства будем записывать это в матричном виде:
. Классическая задача регрессии ставится следующим образом:
.
В силу неточности измерений данных или каких либо еще ошибок с целью построения наилучшей модели вводят регуляризатор или несколько регуляризаторов. Тогда получается следующая задача оптимизации:
.
Частными случаями являются модели лассо () и гребневой регрессии (
).
Для каждого фиксированного
можно перебрать все возможные значения параметра
(поскольку по этому параметру это кусочно-линейная функция с конечным числом точек, в которых она не дифференцируема)[1].
Реализации
- Matlab: Функция lasso, для задания l2 регуляризации есть дополнительный аргумент Alpha[1].
- Python: В пакете sklearn есть библиотека linear_model в которой есть класс ElasticNet[1].
- R: Пакет glmnet[1].
Во всех реализациях используется подход LARS, который как раз и позволяет найти все точки перегиба функционала по .
Также в Matlab и Python есть соответствующие функции для выбора оптимальных значений параметров по кросс-валидации: в Matlab это все та же функция lasso, в Python это класс ElasticNetCV.
Пример
Пример использования Lasso и ElasticNet в Python на данных идущих в комплекте с пакетом SkLearn. В данном примере рассматриваются данные о диабетиках. Собраны данные с 442 пациентов у каждого замерено 10 физиологических признаков, среди которых вес, пол, возраст и давление в крови. В качестве целевого признака известна непрерывная величина характеризующая прогрессивность болезни за последний год. Ставится задача предсказания по физиологическим характеристикам человека прогрессивность болезни. Строится две модели (Lasso),
(Elastic-Net). На графике изображены значения весов обученной модели в зависимости от коэффициента регуляризации
. По графику видно, что веса признаков в эластичной сети в зависимости от L1 регуляризатора более гладкие по сравнению с лассо. Тем не менее можно заметить, что поведение весов очень похоже. Эластичная сеть не так жестко зануляет коэффициенты, то есть они обнулились только в самой левой точке(очень большой регуляризатор).