Графические модели (курс лекций)/2013/Задание 3
Материал из MachineLearning.
(→Рекомендации по выполнению задания) |
(→Формулировка задания) |
||
| Строка 68: | Строка 68: | ||
# Для модели авторегрессии M-го порядка: | # Для модели авторегрессии M-го порядка: | ||
| - | #* Вывести формулы для оценки параметров модели <tex>\vec{w},A,\Sigma</tex> по наблюдениям <tex>\{\vec{x}_n\}_{n=1}^N</tex> с помощью метода максимального правдоподобия; | + | #* Вывести формулы для оценки параметров модели <tex>\vec{w},\mathcal{A},\Sigma</tex> по наблюдениям <tex>\{\vec{x}_n\}_{n=1}^N</tex> с помощью метода максимального правдоподобия; |
#* Реализовать процедуру генерации сигнала из модели авторегрессии; | #* Реализовать процедуру генерации сигнала из модели авторегрессии; | ||
| - | #* Реализовать процедуру оценки параметров <tex>\vec{w},A,\Sigma</tex> по методу максимального правдоподобия; | + | #* Реализовать процедуру оценки параметров <tex>\vec{w},\mathcal{A},\Sigma</tex> по методу максимального правдоподобия; |
#* Реализовать процедуру оценки выборочной автокорреляционной функции остатков авторегрессии; | #* Реализовать процедуру оценки выборочной автокорреляционной функции остатков авторегрессии; | ||
# Провести эксперименты с авторегрессией M-го порядка на модельных данных: | # Провести эксперименты с авторегрессией M-го порядка на модельных данных: | ||
#* в | #* в | ||
# Для авторегрессионной скрытой марковской модели: | # Для авторегрессионной скрытой марковской модели: | ||
| - | #* Вывести формулы ЕМ-алгоритма для оценки параметров модели <tex>\vec{\pi}, | + | #* Вывести формулы ЕМ-алгоритма для оценки параметров модели <tex>\vec{\pi},R,\{\vec{w}_k,\mathcal{A}_k,\Sigma_k}_{k=1}^K</tex>, при этом предусмотреть ситуации, когда часть параметров известна; |
#* Реализовать процедуру генерации сигнала из модели; | #* Реализовать процедуру генерации сигнала из модели; | ||
#* Реализовать процедуру оценки параметров модели с помощью EM-алгоритма; | #* Реализовать процедуру оценки параметров модели с помощью EM-алгоритма; | ||
Версия 22:50, 30 марта 2013
| | Формулировка задания находится в стадии подготовки. Убедительная просьба не приступать к выполнению задания до тех пор, пока это предупреждение не будет удалено. |
Начало выполнения задания: 18 марта 2013 г.;
Срок сдачи: 7 апреля 2013 г. (воскресенье), 23:59.
Среда для выполнения задания — MATLAB. Неэффективная реализация кода может негативно отразиться на оценке.
Содержание |
Модель авторегрессии
Случайный процесс с дискретным временем ,
называется авторегрессией первого порядка, если
.
Здесь ,
,
, шумовые компоненты
являются независимыми. Процесс авторегрессии является стационарным, если все собственные значения матрицы
(включая комплексные) по модулю меньше единицы. Мат.ожидание
стационарного процесса авторегрессии определяется как
,
где — единичная матрица размера
.
В терминах графических моделей авторегрессия первого порядка представляет собой байесовскую сеть с графом вида цепочка (см. рис.), где совместное распределение задается как
,
а — начальная предыстория.
Авторегрессия M-го порядка задается как
.
Здесь шумовые компоненты по-прежнему предполагаются независимыми. Очевидно, что авторегрессия M-го порядка может быть сведена к авторегрессии первого порядка как
Поэтому авторегрессия M-го порядка является стационарной, если все собственные значения матрицы по модулю меньше единицы. Мат.ожидание стационарной регрессии M-го порядка определяется как
.
В дальнейшем для удобства набор матриц будем обозначать через
.
В терминах графических моделей авторегрессия M-го порядка представляет собой байесовскую сеть с графом, показанном на рис. справа, где совместное распределение задается как
,
а — начальная предыстория.
Авторегрессионная скрытая марковская модель
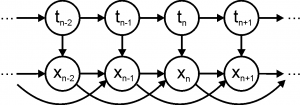
Авторегрессионная скрытая марковская модель M-го порядка — это байесовская сеть, граф которой показан на рис. справа, а совместное распределение задается как
.
Здесь — скрытые дискретные состояния,
— непрерывные наблюдаемые переменные. Априорное распределение
задается вектором
, причем все
и
. Распределение
задается матрицей перехода
размера
, где в
-ой позиции стоит вероятность перехода из состояния
в состояние
. Все элементы этой матрицы неотрицательны, а сумма элементов по каждой строке равна единице. Модель генерации данных соответствует модели авторегрессии, в которой параметры
зависят от текущего состояния
. Таким образом,
.
В результате полный набор параметров модели состоит из . Глубина авторегрессии
, количество скрытых состояний
, а также начальная предыстория
задаются пользователем.
Формулировка задания
- Для модели авторегрессии M-го порядка:
- Вывести формулы для оценки параметров модели
по наблюдениям
с помощью метода максимального правдоподобия;
- Реализовать процедуру генерации сигнала из модели авторегрессии;
- Реализовать процедуру оценки параметров
по методу максимального правдоподобия;
- Реализовать процедуру оценки выборочной автокорреляционной функции остатков авторегрессии;
- Вывести формулы для оценки параметров модели
- Провести эксперименты с авторегрессией M-го порядка на модельных данных:
- в
- Для авторегрессионной скрытой марковской модели:
- Вывести формулы ЕМ-алгоритма для оценки параметров модели
, при этом предусмотреть ситуации, когда часть параметров известна;
- Реализовать процедуру генерации сигнала из модели;
- Реализовать процедуру оценки параметров модели с помощью EM-алгоритма;
- Реализовать процедуру оценки скрытых состояний по наблюдаемым данным и параметрам модели с помощью алгоритма Витерби;
- Вывести формулы ЕМ-алгоритма для оценки параметров модели
- Провести эксперименты с авторегрессионной скрытой марковской моделью на модельных данных:
- Применить авторегрессионную скрытую марковскую модель для моделирования и сегментации движений в базе данных mocap.
Рекомендации по выполнению задания
1. Вывод формул для авторегрессии и авторегрессионной скрытой марковской модели удобно осуществлять путем введения обозначений
Тогда выражение можно лаконично записать как
.
2. При тестировании ЕМ-алгоритма рекомендуется отследить монотонное возрастание логарифма правдоподобия в итерациях.
Оформление задания
Выполненное задание следует отправить письмом по адресу bayesml@gmail.com с заголовком письма «[ГМ13] Задание 3 <ФИО>». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Также убедительная просьба строго придерживаться заданных ниже прототипов реализуемых функций.
Присланный вариант задания должен содержать в себе:
- Файл отчёта в формате PDF с указанием ФИО.
- Все исходные коды с необходимыми комментариями.
| Генерация выборки из модели авторегрессии | |||||
|---|---|---|---|---|---|
| X = ar_generate(N, w, A, Sigma, X0) | |||||
| ВХОД | |||||
| |||||
| ВЫХОД | |||||
|
Если начальная предыстория не задана, то
выбирается равной мат.ожиданию процесса авторегрессии.
| Оценка параметров авторегрессии | |||||
|---|---|---|---|---|---|
| [w, A, Sigma, res, LH] = ar_fit(X, M) | |||||
| ВХОД | |||||
| |||||
| ВЫХОД | |||||
|
| Генерация выборки из авторегрессионной скрытой марковской модели | |||||||
|---|---|---|---|---|---|---|---|
| [X, T] = arhmm_generate(N, p, R, W, A, Sigmas, X0) | |||||||
| ВХОД | |||||||
| |||||||
| ВЫХОД | |||||||
|
Если начальная предыстория не задана, то
выбирается равной мат.ожиданию процесса авторегрессии, соответствующего сгенерированному состоянию
.
| Оценка параметров авторегрессионной скрытой марковской модели с помощью ЕМ-алгоритма | |||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [p, R, W, A, Sigmas] = arhmm_fit(X, K, M, param_name1, param_value1, ...) | |||||||||||||||||||||||||||||||||
| ВХОД | |||||||||||||||||||||||||||||||||
|