Оптимальное прореживание нейронных сетей (пример)
Материал из MachineLearning.
(→Использованная литература: ссылки на участников) |
(→Исходный код) |
||
| Строка 507: | Строка 507: | ||
==Исходный код== | ==Исходный код== | ||
| - | Листинги алгоритмов можно посмотреть здесь:[http://mlalgorithms.svn.sourceforge.net/viewvc/mlalgorithms arglayer.m,backprop.m,damage.m, | + | Листинги алгоритмов можно посмотреть здесь:[http://mlalgorithms.svn.sourceforge.net/viewvc/mlalgorithms/Yudaev2010GAP/ arglayer.m], |
| + | [http://mlalgorithms.svn.sourceforge.net/viewvc/mlalgorithms/Yudaev2010GAP/ backprop.m], | ||
| + | [http://mlalgorithms.svn.sourceforge.net/viewvc/mlalgorithms/Yudaev2010GAP/ damage.m], | ||
| + | [http://mlalgorithms.svn.sourceforge.net/viewvc/mlalgorithms/Yudaev2010GAP/ featuredamage.m]. | ||
| + | |||
==См. также== | ==См. также== | ||
*[[Оптимальное прореживание нейронных сетей]] | *[[Оптимальное прореживание нейронных сетей]] | ||
Версия 08:39, 12 марта 2012
Содержание |
Постановка задачи
Рассматривается двухслойная нейронная сеть с одним выпускающим нейроном и заведомо достаточно сложной для выбранной задачи топологией. Производится упрощение её структуры путём разрезания наименее значимых связей для повышения обобщающей способности, пока не начнут ухудшаться результаты на контрольной выборке. Наименее значимые связи определяются через приближение гессиана функции потерь
в задаче разделения на 2 класса. Используется дифференцируемое приближение
функции потерь
,
где
- отступ (margin) нейронной сети на объекте
,
- вес соответствующей ошибки,
- сигмоидная функция.
Теория
Если функционал качества Q в некоторой точке достаточное число раз дифференцируем(3 раза), то его можно представить в окрестности этой точки в виде
,
где
- гессиан функции потерь.
Если считать, что после обучения веса нейросети w соответствуют локальному минимуму функционала качества Q, то в этой точке
, и приращение фнкции потерь можно считать равным
.
Теперь пусть
-некий синаптический вес, его обнуление эквивалентно выполнению
, где
- i-й столбец единичной матрицы порядка, равного размерности вектора весов нейросети.
Получаем задачу условной минимизации :
Лагранжиан
.
Решая её, получим оптимальное изменение весов
и соответствующее приращение лагранжиана(степень выпуклости, она же значимость, salency)
.
Для разрезания выбираются веса с наименьшей степенью выпуклости. В процедуре OBD, кроме того, предполагается существенное диагональное преобладание гессиана в локальном минимуме так, что можно пренебречь недиагональными элементами, и полученное соотношение для степени выпуклости вырождается в
.
Методы
В данном прмере для минимизации дифференцируемой модификации функции потерь применяется процедура наискорейшего градиентного спуска с вычислением градиента методом обратного распространения ошибки(back propagation) с мультистартом. Темп обучения на каждом шаге ищется одномерной минимизацией функции потерь в направлении антиградиента с помощью функции Matlab fminbnd. Обучение останавливается, когда найденный таким образом на очередной итерации темп обучения стновится меньше критического значения().
Вторые производные функционала качества по весам(диагональные элементы гессиана) ищутся разностным методом
.
На каждом шаге Optimal Brain Damage разрезается ровно 1 синаптический вес до тех пор, пока после очередного разрезания и последующего обучения 2 раза подряд не увеличится значение функции потерь на контрольной выборке.
На модельных данных
Для апробации алгоритма на модельных данных были сгенерированы ( GetNormClass.m) 2 сильно пересекающихся нормально распределённых 10-мерных класса, затем полученная выборка случайным образом поделена на обучающую и контрольную, и с ними поизведены описанные операции над двухслойным персептроном с 10-тью нейронами в каждом скрытом слое. В таблице приведён порядок разрезания синапсов и динамика функционала качества (в % от максимально возможных потерь).
| номер слоя | испускающий нейрон | принимающий нейрон | степень выпуклости(salency) | качество на обучении(после разрезания) | качество на контроле(после разрезания) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 5.7553 | 1.4085 |
| 3 | 2 | 1 | -0.1482 | 10.0719 | 8.4507 |
| 1 | 9 | 1 | -0.0068 | 10.0719 | 8.4507 |
| 1 | 2 | 3 | -0.1248 | 9.3525 | 22.5352 |
| 1 | 9 | 9 | -0.0819 | 10.0719 | 15.4930 |
| 3 | -1 | 1 | -0.0278 | 9.3525 | 22.5352 |
| 1 | 3 | 9 | -0.025 | 8.6331 | 21.1268 |
| 1 | 5 | 4 | -9.5465e-4 | 8.6331 | 21.1268 |
| 1 | 6 | 9 | -0.0021 | 8.6331 | 15.493 |
| 1 | 3 | 5 | -0.0074 | 28.0576 | 42.2535 |
| 1 | 5 | 5 | -0.0115 | 3.5971 | 21.1268 |
| 1 | 5 | 2 | -0.0012 | 3.5971 | 21.1268 |
| 2 | 1 | 4 | -0.0086 | 5.036 | 8.4507 |
| 2 | 8 | 8 | -0.0055 | 17.2662 | 35.2113 |
| 1 | 8 | 9 | -0.0288 | 8.6331 | 22.5352 |
| 1 | 4 | 1 | -0.0049 | 12.9496 | 21.1268 |
| 1 | 1 | 10 | -0.0167 | 11.5108 | 22.5352 |
| 1 | 6 | 1 | -0.0021 | 13.6691 | 28.169 |
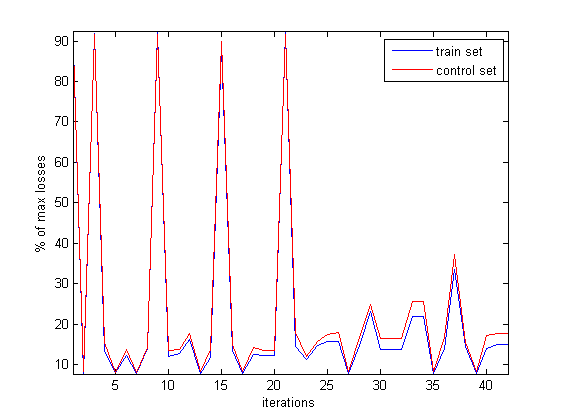
На рисунке показана динамика изменения функции потерь при разрезании синапсов и последующем обучении(синим - на обучении, красным - на контроле).
German Credit Data
Та же процедура проделана на данных кредитного скоринга [1]. Как видно из динамики функции потерь и характеристик разрезаемых синапсов, OBD почти не улучшает качество сети на контольной выборке, из чего можно сделать вывод о низкой степени переобучения, обусловленной, возможно, низкой эффективностью применяемого алгоритма обучения для данного случая.
| номер слоя | испускающий нейрон | принимающий нейрон | степень выпуклости(salency) | качество на обучении(после разрезания) | качество на контроле(после разрезания) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 7.6722 | 8.2447 |
| 2 | -1 | 2 | -0.7672 | 13.2859 | 15.4255 |
| 1 | 10 | 1 | -0.0324 | 12.238 | 13.7411 |
| 2 | 3 | 6 | -0.0149 | 14.0719 | 14.1844 |
| 3 | 4 | 1 | -1.0912e-8 | 12.0509 | 13.3865 |
| 1 | 4 | 3 | -8.8795e-4 | 16.1677 | 17.7305 |
| 1 | 2 | 1 | -0.0118 | 11.7889 | 13.8298 |
| 2 | 1 | 7 | -0.0109 | 13.5479 | 14.9823 |
| 2 | 5 | 6 | -0.0282 | 12.3877 | 14.273 |
| 1 | 10 | 5 | -9.9848e-4 | 12.3503 | 13.3865 |
| 3 | 10 | 1 | -0.0815 | 14.5958 | 17.9078 |
| 1 | 4 | 1 | -0.0115 | 14.6707 | 15.6915 |
| 1 | 4 | 10 | -0.0017 | 15.8308 | 17.9078 |
| 1 | -1 | 3 | -0.1207 | 14.6707 | 16.578 |
| 1 | 2 | 3 | -0.0214 | 13.6228 | 16.4894 |
| 1 | 8 | 10 | -1.4583e-7 | 13.6228 | 16.4894 |
| 1 | 4 | 2 | -0.0067 | 21.9311 | 25.6206 |
| 1 | -1 | 5 | -0.1584 | 13.9596 | 16.7553 |
| 1 | 4 | 5 | -0.0143 | 14.3713 | 15.4255 |
| 3 | 6 | 1 | -2.0273e-7 | 13.9596 | 17.2872 |
| 1 | 19 | 6 | -1.5601e-5 | 14.8952 | 17.6418 |
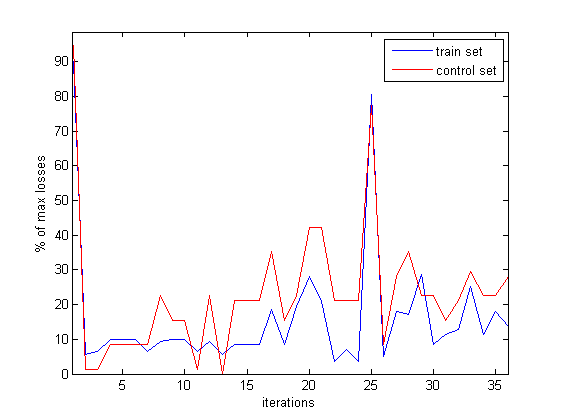
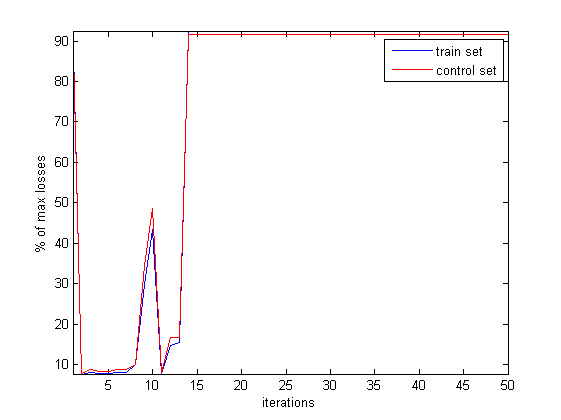
Внизу динамика функции потерь с учётом состояний сразу после разрезания и без их учёта.
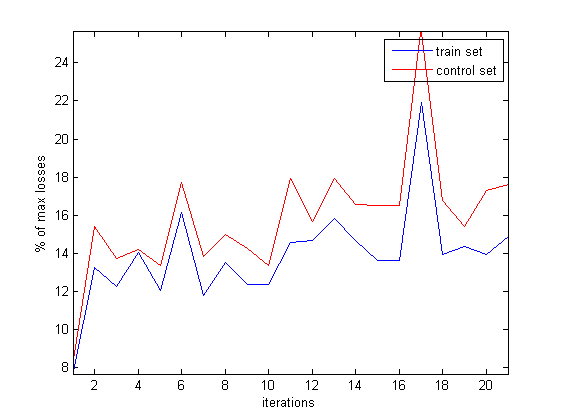
Далее показана динамика качества сети до существенного увеличения потерь без учёта состояний сразу после разрезания.
Отбор признаков
Процедура OBD может также применяться для отбора признаков в модели, точнеее, для удаления наименее информативных признаков. Обычно в таких случаях находят суммарную степень выпуклости весов синапсов, идущих от каждого признака, называемую также значимостью(salency) признака:
, где P - число нейронов в первом слое.
После чего разрезают все синапсы от признака, у которого это значение получилось наименьшим.
| № удаляемого признака | значение("-"-не указано) | степень значимости(salency) | потери на обучении(после удаления) | потери на контроле(после удаления) |
|---|---|---|---|---|
| 0 | - | 0 | 7.5599 | 8.2447 |
| 20 | является ли иностранцем | 3.0208e5 | 7.5599 | 8.2447 |
| 8 | размер 1 выплаты в % от разового дохода | 1.8815e5 | 7.6722 | 8.2447 |
| 16 | количество непогашенных ссуд в данном банке | 5.9898e5 | 13.2111 | 13.2979 |
| 4 | на что берётся ссуда(автомобиль,мебель,образование,...) | -1.2521e6 | 12.762 | 13.7411 |
| 12 | тип закладываемой собственности | 1.3485e5 | 12.0883 | 15.6915 |
| 9 | пол и семейное положение | -1.0977e-5 | 14.0344 | 17.1986 |
| 10 | наличие поручителей | -2.5131e6 | 12.3877 | 12.5 |
| 11 | срок проживания по текущему адресу | 9.3062e-7 | 15.2695 | 14.805 |
| 2 | срок погашения | -3.5434e5 | 8.7575 | 9.3972 |
| 6 | размер сбережений | 2.5018e5 | 8.1961 | 8.7766 |
| 15 | вид собственности на жильё | 9.1573e5 | 12.8368 | 15.5142 |
| 3 | наличие погашенных/непогашенных ссуд | 1.1045e5 | 12.7994 | 15.0709 |
| 1 | объём средст на текущем счёте | -1.3721e5 | 14.6332 | 13.8298 |
| 7 | срок работы на нынешнем месте | 2.0617e5 | 8.6078 | 8.6879 |
| 17 | профессиональный статус | 9.1559e5 | 14.2964 | 11.5248 |
| 14 | другие предполагаемые платежи(на период выплаты ссуды) | 1.0234e6 | 14.5584 | 11.4362 |
| 18 | число людей, способных подтвердить данные в анкете | 2.1884e5 | 13.0614 | 10.195 |
| 23 | - | 1.0408e6 | 14.5958 | 11.9681 |
| 13 | возраст | 1.8521e6 | 14.7455 | 11.4362 |
| 19 | наличие телефона, зарегистрированного на имя клиента | -1.7914e6 | 14.521 | 11.4362 |
| 5 | размер ссуды | 3.0175e5 | 14.2216 | 12.5 |
| 22 | - | 1.2204e6 | 14.4461 | 12.6773 |
| 21 | - | -3.8515e5 | 14.4087 | 10.9043 |
| 24 | - | -1.737e6 | 7.747 | 8.2447 |
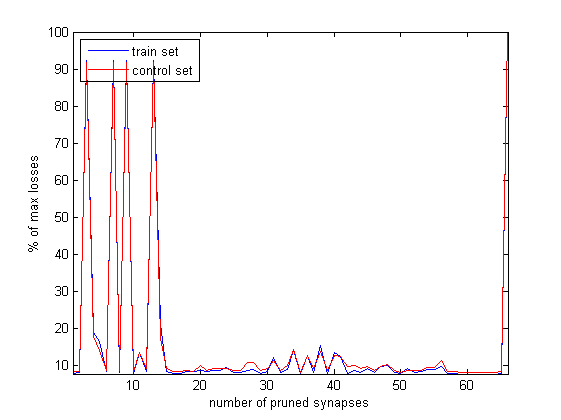
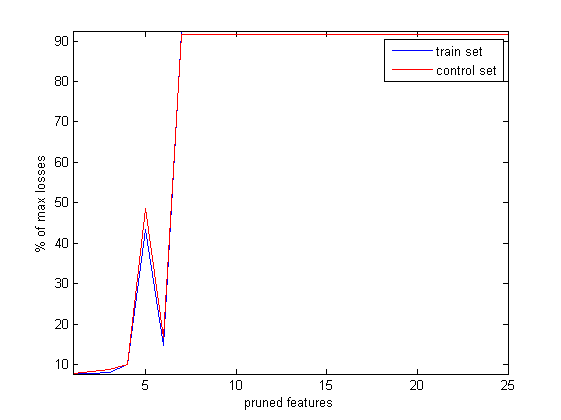
Далее приведена динамика функции потерь при разрезании признаков с учётом состояний сразу после разрезания и без их учёта.
Исходный код
Листинги алгоритмов можно посмотреть здесь:arglayer.m, backprop.m, damage.m, featuredamage.m.
См. также
- Оптимальное прореживание нейронных сетей
- Вычисление матриц Якоби и Гессе
- Прореживание двухслойной нейронной сети (пример)
Использованная литература
- 1. Хайкин С. Нейронные сети, полный курс. 2е издание, испр. - М: Вильямс. 2008. - 1103 с. ISBN 978-5-8459-0890-2
- 2. Bishop Ch.M. Neural Networks for Pattern Recognition. - Oxford: Clarendon Press.1995.
- 3. Воронцов К.В. Машинное обучение. Лекции.
| | Данная статья была создана в рамках учебного задания.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |