Участник:Anton/Песочница

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
Строка 7: Строка 7:
=== Формулировка задания ===
=== Формулировка задания ===
-
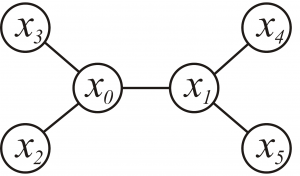
[[Изображение:sinc_rvr.jpg|150px|thumb|Пример решения задачи регрессии: восстановление зашумленной функции sinc]]
+
[[Изображение:GraphicalModels2012_hw1_image1.png|300px|thumb|Система соседства марковской сети.]]
 +
 
 +
Рассматривается марковская сеть из 6 переменных: <tex>x_0, x_1, x_2, x_3, x_4, x_5</tex>.
 +
Энергия системы задается следующим образом:<br>
 +
<tex>
 +
E(x_0, \dots, x_5) = \sum_{i = 1}^5 \varphi_i(x_i) + \sum_{(i, j) \in \mathcal{E}} \varphi_{ij}(x_i, x_j).
 +
</tex>
 +
 
 +
Множества значений переменных: <tex>x_0, x_1 \in \{0, 1 \}; \quad x_2, x_3, x_4, x_5 \in \{0, 1, 2 \}.</tex>
Рассматривается классическая скрытая марковская модель (СММ) первого порядка, в которой полное правдоподобие задается как:
Рассматривается классическая скрытая марковская модель (СММ) первого порядка, в которой полное правдоподобие задается как:

Версия 13:28, 28 февраля 2012

Перейти к основной странице курса

Начало выполнения задания: 29 февраля 2012

Срок сдачи: 7 марта 2012, 18:00


Формулировка задания

Система соседства марковской сети.
Система соседства марковской сети.

Рассматривается марковская сеть из 6 переменных: x_0, x_1, x_2, x_3, x_4, x_5. Энергия системы задается следующим образом:
E(x_0, \dots, x_5) = \sum_{i = 1}^5 \varphi_i(x_i) + \sum_{(i, j) \in \mathcal{E}} \varphi_{ij}(x_i, x_j).

Множества значений переменных: x_0, x_1 \in \{0, 1 \}; \quad x_2, x_3, x_4, x_5 \in \{0, 1, 2 \}.

Рассматривается классическая скрытая марковская модель (СММ) первого порядка, в которой полное правдоподобие задается как:

p(X,T|\theta)=p(t_1)\prod_{n=2}^Np(t_n |t_{n-1})\prod_{n=1}^Np(x_n |t_n )


Оформление задания

Выполненный вариант задания необходимо прислать письмом по адресу bayesml@gmail.com с темой «Задание 1. ФИО, номер группы». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Также убедительная просьба строго придерживаться заданной выше спецификации реализуемых функций. Очень трудно проверять большое количество заданий, если у каждого будет свой формат реализации.

Письмо должно содержать:

  • PDF-файл с описанием проведенных исследований
  • LDS_GENERATE.m
  • LDS_forwardbackward.m
  • LDS_EM_TRAIN.m
  • TRAJECTORY_GENERATE.m
  • Ссылка на видео-файл, размещенный на файлообменнике или на видео-хостинге, с наложенными исходной и фильтрованной траекториями движения центра масс мыши. Лучше вставить видео-файл непосредственно внутрь PDF-файла с отчетом (это можно сделать, например, в программе Adobe Acrobat 9 и выше). Тогда нужно прислать ссылку на этот PDF-файл.
  • Набор вспомогательных файлов при необходимости
Источник — «http://recognition.su/wiki/index.php?title=%D0%A3%D1%87%D0%B0%D1%81%D1%82%D0%BD%D0%B8%D0%BA:Anton/%D0%9F%D0%B5%D1%81%D0%BE%D1%87%D0%BD%D0%B8%D1%86%D0%B0»
Личные инструменты