Модель МакКаллока-Питтса
Материал из MachineLearning.
(категория) |
|||
| (18 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
| - | + | {{TOCright}} | |
| + | Первой формальной моделью [[Нейронная сеть| нейронных сетей]] (НС) была модель МакКаллока-Питтса, уточненная и развитая Клини. Впервые было установлено, что НС могут выполнять любые логические операции и вообще любые преобразования, реализуемые дискретными устройствами с конечной памятью. Эта модель легла в основу теории логических сетей и конечных автоматов и активно использовалась психологами и нейрофизиологами при моделировании некоторых локальных процессов нервной деятельности. В силу своей дискретности она вполне согласуется с компьютерной парадигмой и, более того, служит её «нейронным фундаментом». | ||
| - | + | =Устройство модели= | |
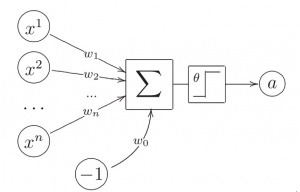
| + | [[Изображение:pict1.jpg|300px|thumb|Рис.1 модель нейрона МакКалока-Питтса]] | ||
| + | Пусть имеется <tex>n</tex> входных величин x<sub>1</sub>,…,x<sub>n</sub> бинарных признаков, описывающих объект <tex>x</tex>. | ||
| + | Значения этих признаков будем трактовать как величины импульсов, поступающих на вход нейрона через <tex>n</tex> входных синапсов. | ||
| + | Будем считать, что, попадая в нейрон, импульсы складываются с весами ω<sub>1</sub>,…,ω<sub>n</sub>. | ||
| - | + | Если вес положительный, то соответствующий синапс возбуждающий, если отрицательный, то тормозящий. | |
| - | + | Если суммарный импульс превышает заданный порог активации ω<sub>0</sub>, то нейрон возбуждается и выдаёт на выходе 1, иначе выдаётся 0. | |
| - | + | ||
| - | + | ||
| - | <center><tex> | + | Таким образом, нейрон вычисляет n-арную булеву функцию |
| + | <center><tex>a(x) = \varphi(\sum_{j=1}^n \omega_jx^j - \omega_0)</tex></center> | ||
| + | где <tex>\varphi(z) = [z \ge 0]</tex> - ступенчатая функция Хевисайда. | ||
| - | + | В теории нейронных сетей функцию φ, преобразующую значение суммарного импульса в выходное значение нейрона, принято называть функцией активации. | |
| + | Таким образом, модель МакКаллока-Питтса эквивалентна пороговому [[Линейный классификатор| линейному классификатору]]. | ||
| + | =Результаты теории= | ||
| + | Теоретические основы нейроматематики были заложены в начале 40-х годов и в 1943 году У. МакКалок и его ученик У. Питтс сформулировали основные положения теории деятельности головного мозга. | ||
| + | Ими были получены следующие результаты: | ||
| + | *разработана модель нейрона как простейшего процессорного элемента, выполняющего вычисление переходной функции от скалярного произведения вектора входных сигналов и вектора весовых коэффициентов; | ||
| + | *предложена конструкция сети таких элементов для выполнения логических и арифметических операций; | ||
| + | *сделано основополагающее предположение о том, что такая сеть способна обучаться, распознавать образы, обобщать полученную информацию. | ||
| - | + | =Недостатки модели= | |
| - | - | + | Недостатком данной модели является сама модель нейрона «пороговой» вид переходной функции. В формализме У. Маккалока-Питтса нейроны имеют состояния 0, 1 и пороговую логику перехода из состояния в состояние. Каждый нейрон в сети определяет взвешенную сумму состояний всех других нейронов и сравнивает ее с порогом, чтобы определить свое собственное состояние. |
| - | + | ||
| - | + | Пороговый вид функции не предоставляет нейронной сети достаточную гибкость при обучении и настройке на заданную задачу. Если значение вычисленного скалярного произведения, даже незначительно, не достигает до заданного порога, то выходной сигнал не формируется вовсе и нейрон «не срабатывает». Это значит, что теряется интенсивность выходного сигнала (аксона) данного нейрона и, следовательно, формируется невысокое значение уровня на взвешенных входах в следующем слое нейронов. | |
| - | + | К тому же модель не учитывает многих особенностей работы реальных нейронов (импульсного характера активности, нелинейности суммирования входной информации, рефрактерности). | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
---- | ---- | ||
| + | Несмотря на то, что за прошедшие годы нейроматематика ушла далеко вперед, многие утверждения МакКалока остаются актуальными и поныне. В частности, при большом разнообразии моделей нейронов принцип их действия, заложенный МакКалоком и Питтсом, остается неизменным. | ||
| - | + | = См. также = | |
| - | + | * [[Персептрон]] | |
| - | + | * [[Перcептрон Розенблатта]] | |
| - | + | * [[Правила Хэбба]] | |
| - | + | * [[Адаптивный линейный элемент]] | |
| - | + | * [[Искусственная нейронная сеть]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | [[ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | [[ | + | |
| - | + | ||
| - | [[ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
=Литература= | =Литература= | ||
| - | + | #[[Машинное обучение (курс лекций, К.В.Воронцов)]] | |
| - | + | #Дж. фон Нейман Теория самовоспроизводящихся автоматов/ закончено и отредактировано А. Бёрксом. - М.: Мир, 1971. - 384 с | |
| - | + | #Маккалох Дж., Питтс У. Логические исчисления идей, относящихся к нервной деятельности.// Автоматы. М.: ИЛ, 1956. | |
| - | + | #http://bio-net.by.ru/public/model_net_rus.pdf | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | =Ссылки= | ||
| + | *http://www.twirpx.com/file/95289/ | ||
| + | *http://dfe.karelia.ru/koi/posob/optproc/neucom.html | ||
| - | [[Категория: | + | [[Категория:Линейные классификаторы]] |
| + | [[Категория:Нейронные сети]] | ||
| + | {{Задание|Platonova.Elena|Константин Воронцов|8 января 2010}} | ||
Текущая версия
|
Первой формальной моделью нейронных сетей (НС) была модель МакКаллока-Питтса, уточненная и развитая Клини. Впервые было установлено, что НС могут выполнять любые логические операции и вообще любые преобразования, реализуемые дискретными устройствами с конечной памятью. Эта модель легла в основу теории логических сетей и конечных автоматов и активно использовалась психологами и нейрофизиологами при моделировании некоторых локальных процессов нервной деятельности. В силу своей дискретности она вполне согласуется с компьютерной парадигмой и, более того, служит её «нейронным фундаментом».
Устройство модели
Пусть имеется входных величин x1,…,xn бинарных признаков, описывающих объект
.
Значения этих признаков будем трактовать как величины импульсов, поступающих на вход нейрона через
входных синапсов.
Будем считать, что, попадая в нейрон, импульсы складываются с весами ω1,…,ωn.
Если вес положительный, то соответствующий синапс возбуждающий, если отрицательный, то тормозящий. Если суммарный импульс превышает заданный порог активации ω0, то нейрон возбуждается и выдаёт на выходе 1, иначе выдаётся 0.
Таким образом, нейрон вычисляет n-арную булеву функцию
где - ступенчатая функция Хевисайда.
В теории нейронных сетей функцию φ, преобразующую значение суммарного импульса в выходное значение нейрона, принято называть функцией активации. Таким образом, модель МакКаллока-Питтса эквивалентна пороговому линейному классификатору.
Результаты теории
Теоретические основы нейроматематики были заложены в начале 40-х годов и в 1943 году У. МакКалок и его ученик У. Питтс сформулировали основные положения теории деятельности головного мозга.
Ими были получены следующие результаты:
- разработана модель нейрона как простейшего процессорного элемента, выполняющего вычисление переходной функции от скалярного произведения вектора входных сигналов и вектора весовых коэффициентов;
- предложена конструкция сети таких элементов для выполнения логических и арифметических операций;
- сделано основополагающее предположение о том, что такая сеть способна обучаться, распознавать образы, обобщать полученную информацию.
Недостатки модели
Недостатком данной модели является сама модель нейрона «пороговой» вид переходной функции. В формализме У. Маккалока-Питтса нейроны имеют состояния 0, 1 и пороговую логику перехода из состояния в состояние. Каждый нейрон в сети определяет взвешенную сумму состояний всех других нейронов и сравнивает ее с порогом, чтобы определить свое собственное состояние.
Пороговый вид функции не предоставляет нейронной сети достаточную гибкость при обучении и настройке на заданную задачу. Если значение вычисленного скалярного произведения, даже незначительно, не достигает до заданного порога, то выходной сигнал не формируется вовсе и нейрон «не срабатывает». Это значит, что теряется интенсивность выходного сигнала (аксона) данного нейрона и, следовательно, формируется невысокое значение уровня на взвешенных входах в следующем слое нейронов.
К тому же модель не учитывает многих особенностей работы реальных нейронов (импульсного характера активности, нелинейности суммирования входной информации, рефрактерности).
Несмотря на то, что за прошедшие годы нейроматематика ушла далеко вперед, многие утверждения МакКалока остаются актуальными и поныне. В частности, при большом разнообразии моделей нейронов принцип их действия, заложенный МакКалоком и Питтсом, остается неизменным.
См. также
- Персептрон
- Перcептрон Розенблатта
- Правила Хэбба
- Адаптивный линейный элемент
- Искусственная нейронная сеть
Литература
- Машинное обучение (курс лекций, К.В.Воронцов)
- Дж. фон Нейман Теория самовоспроизводящихся автоматов/ закончено и отредактировано А. Бёрксом. - М.: Мир, 1971. - 384 с
- Маккалох Дж., Питтс У. Логические исчисления идей, относящихся к нервной деятельности.// Автоматы. М.: ИЛ, 1956.
- http://bio-net.by.ru/public/model_net_rus.pdf
Ссылки
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |